好朋友Z说他们期末得设计一个计算器,对数ln的运算挺麻烦的。
我想,这不是就是泰勒展开的事吗?
泰勒展开1.0
立刻想到了这个嘛:
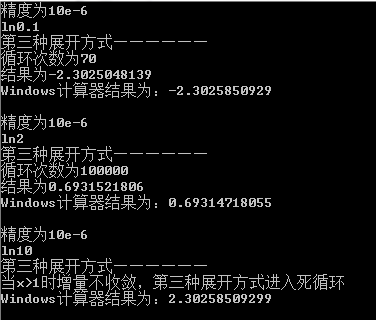
然而,跑一下程序的结果是这样的:
1.1 循环的次数多——Peano余项为o(x^n),收敛的速度慢;x越接近2,收敛就越慢。
1.2 当x>1时,增量不收敛,然后答案跑不出来了= =
因为设置的跳出循环的条件为:
while(fabs(delta/i)>Epsilon)所以这样展开将进入死循环
面对这1.1和1.2两个缺陷,我不由得觉得自己最开始想得太天真。
泰勒展开2.0
教材上的一道例题——提高ln2的求解精度,同时解释了1.0泰勒展开的缺陷:








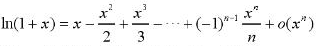
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 138
138

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








