最小生成树

最小生成树

1. 问题

如何求一个包含有原图所有n个结点的且所有边的代价和最小的极小连通子图。

2.解析

kruskal：

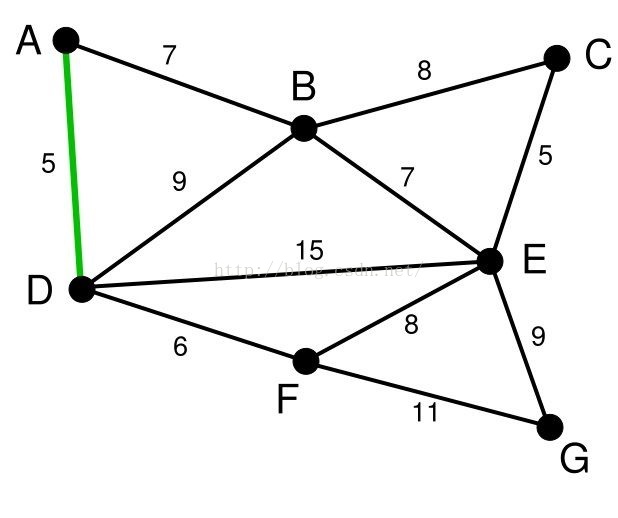
Kruskal算法是基于贪心的思想得到的。首先我们把所有的边按照权值先从小到大排列，接着按照顺序选取每条边，如果这条边的两个端点不属于同一集合，那么就将它们合并，直到所有的点都属于同一个集合为止。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-RCP8ioKR-1623764171439)(https://z3.ax1x.com/2021/05/17/g2jJtH.jpg)]

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-AduAScUl-1623764171443)(https://z3.ax1x.com/2021/05/17/g2jU1I.jpg)]
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-AAIchRjt-1623764171444)(https://z3.ax1x.com/2021/05/17/g2jYhd.jpg)]

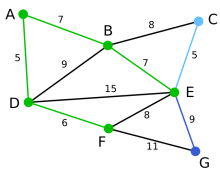
Prim:

输入：一个加权连通图，其中顶点集合为V，边集合为E；

初始化：Vnew = {x}，其中x为集合V中的任一节点（起始点），Enew = {},为空；

重复下列操作，直到Vnew = V：

在集合E中选取权值最小的边<u, v>，其中u为集合Vnew中的元素，而v不在Vnew集合当中，并且v∈V（如果存在有多条满足前述条件即具有相同权值的边，则可任意选取其中之一）；

将v加入集合Vnew中，将<u, v>边加入集合Enew中；

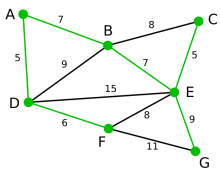
输出：使用集合Vnew和Enew来描述所得到的最小生成树。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-9UfD5bWS-1623764171446)(https://z3.ax1x.com/2021/05/17/g2vPCd.png)]

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-YhsoIsHB-1623764171447)(https://z3.ax1x.com/2021/05/17/g2v94H.png)]
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-OxA59Shy-1623764171448)(https://z3.ax1x.com/2021/05/17/g2vi8A.png)]
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-MCTvWLvV-1623764171449)(https://z3.ax1x.com/2021/05/17/g2vpUe.png)]
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-SNiBZ6nb-1623764171450)(https://z3.ax1x.com/2021/05/17/g2vSED.png)]

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-HbL92dg3-1623764171452)(https://z3.ax1x.com/2021/05/17/g2vkvt.png)]

3.设计

Kruskal:

void Kruskal(MatGraph g)
{  int i,j,u1,v1,sn1,sn2,k;
   int v[MAXV];
   Edge E[MaxSize];		//存放所有边
   k=0;				//E数组的下标从0开始计
   for (i=0;i<g.n;i++)	//由g产生的边集E
     for (j=0;j<g.n;j++)
        if (g.edges[i][j]!=0 && g.edges[i][j]!=INF)
	 {  E[k].u=i;  E[k].v=j;  E[k].w=g.edges[i][j];
	    k++;
	 }
   InsertSort(E,g.e);		//用直接插入排序对E数组按权值递增排序
   for (i=0;i<g.n;i++) 	//初始化辅助数组
	v[i]=i;
    k=1;				//k表示当前构造生成树的第几条边
    j=0;				//E中边的下标，初值为0
while (k<g.n)		//生成的边数小于n时循环
  { 
     u1=E[j].u;v1=E[j].v;	//取一条边的头尾顶点
     sn1=v[u1];
     sn2=v[v1];		//分别得到两个顶点所属的集合编号
     if (sn1!=sn2)  		//两顶点属于不同的集合
     {  printf("  (%d，%d):%d\n",u1,v1,E[j].w);
        k++;		   	//生成边数增1
        for (i=0;i<g.n;i++)  	//两个集合统一编号
           if (v[i]==sn2) 	//集合编号为sn2的改为sn1
		        v[i]=sn1;
     }
     j++;			//扫描下一条边
  }
}

Prim:

void prim(Graph G, int start)
{
    int min,i,j,k,m,n,sum;
    int index=0;         // prim最小树的索引，即prims数组的索引
    char result[MAX];     // prim最小树的结果数组
    int weights[MAX];    // 顶点间边的权值
 
    // prim最小生成树中第一个数是"图中第start个顶点"，因为是从start开始的。
    result[index++] = G.vexs[start];
 
    // 初始化"顶点的权值数组"，
    // 将每个顶点的权值初始化为"第start个顶点"到"该顶点"的权值。
    for (i = 0; i < G.vexnum; i++ )
        weights[i] = G.matrix[start][i];
    // 将第start个顶点的权值初始化为0。
    // 可以理解为"第start个顶点到它自身的距离为0"。
    weights[start] = 0;
 
    for (i = 0; i < G.vexnum; i++)
    {
        // 由于从start开始的，因此不需要再对第start个顶点进行处理。
        if(start == i)
            continue;
 
        j = 0;
        k = 0;
        min = INF;
        // 在未被加入到最小生成树的顶点中，找出权值最小的顶点。
        while (j < G.vexnum)
        {
            // 若weights[j]=0，意味着"第j个节点已经被排序过"(或者说已经加入了最小生成树中)。
            if (weights[j] != 0 && weights[j] < min)
            {
                min = weights[j];
                k = j;
            }
            j++;
        }
 
        // 经过上面的处理后，在未被加入到最小生成树的顶点中，权值最小的顶点是第k个顶点。
        // 将第k个顶点加入到最小生成树的结果数组中
        result[index++] = G.vexs[k];
        // 将"第k个顶点的权值"标记为0，意味着第k个顶点已经排序过了(或者说已经加入了最小树结果中)。
        weights[k] = 0;
        // 当第k个顶点被加入到最小生成树的结果数组中之后，更新其它顶点的权值。
        for (j = 0 ; j < G.vexnum; j++)
        {
            // 当第j个节点没有被处理，并且需要更新时才被更新。
            if (weights[j] != 0 && G.matrix[k][j] < weights[j])
                weights[j] = G.matrix[k][j];
        }
    }
 
    // 计算最小生成树的权值
    sum = 0;
    for (i = 1; i < index; i++)
    {
        min = INF;
        // 获取result[i]在G中的位置
        n = get_position(G, result[i]);
        // 在vexs[0...i]中，找出到j的权值最小的顶点。
        for (j = 0; j < i; j++)
        {
            m = get_position(G, result[j]);
            if (G.matrix[m][n]<min)
                min = G.matrix[m][n];
        }
        sum += min;
    }
    // 打印最小生成树
    printf("PRIM(%c)=%d: ", G.vexs[start], sum);
    for (i = 0; i < index; i++)
        printf("%c ", result[i]);
    printf("\n");
}

4.分析

Prim算法是通过不断取距离最近的点来生成最小生成树，所以时间复杂和点有关，时间复杂度为T=O（n^2），更适用于稠密图。
Kruskal算法是基于并查集的思想，通过不断收取权值最小的边来得到最小生成树，所以时间复杂度和边有关，时间复杂度为T=（nlogn），更适用于稀疏图。
``

4.分析

Prim算法是通过不断取距离最近的点来生成最小生成树，所以时间复杂和点有关，时间复杂度为T=O（n^2），更适用于稠密图。
Kruskal算法是基于并查集的思想，通过不断收取权值最小的边来得到最小生成树，所以时间复杂度和边有关，时间复杂度为T=（nlogn），更适用于稀疏图。