在数论中,特别在同余理论里,一个整数 对另一个整数
对另一个整数 的二次剩余(英语:Quadratic residue)指
的二次剩余(英语:Quadratic residue)指 的平方
的平方 除以
除以 得到的余数。
得到的余数。
当存在某个 ,式子
,式子 成立时,称“
成立时,称“ 是模
是模 的二次剩余”
的二次剩余”
当对任意 ,
, 不成立时,称“d是模p的二次非剩余”
不成立时,称“d是模p的二次非剩余”
质数的二次剩余
对于质数2,每个整数都是它的二次剩余。
以下讨论 是奇质数的情况:
是奇质数的情况:
对于 ,
, 而言,能满足“
而言,能满足“ 是模
是模  的二次剩余”的
的二次剩余”的  共有
共有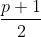 个(剩余类),分别为:
个(剩余类),分别为: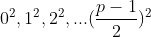 (0计算在内)
(0计算在内)
此外是 个二次非剩余。
个二次非剩余。但在很多情况下,我们只考虑乘法群Z/pZ,因此不将0包括在内。这样,每个二次剩余的乘法逆元仍然是二次剩余;二次非剩余的乘法逆元仍然是二次非剩余。
二次剩余的个数与二次非剩余的个数相等,都是 。此外,两个二次非剩余的乘积是二次剩余,二次剩余和二次非剩余的乘积是二次非剩余。
。此外,两个二次非剩余的乘积是二次剩余,二次剩余和二次非剩余的乘积是二次非剩余。
应用二次互反论可以知道,当 模4余1时,-1是
模4余1时,-1是 的二次剩余;如果
的二次剩余;如果 模4余3,那么,-1是
模4余3,那么,-1是 的二次非剩余。
的二次非剩余。
要知道d是否为模p的二次剩余,可以运用欧拉判别法(或叫欧拉准则)。
另外,若找到一个a,使得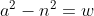 ,且
,且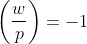 ,则
,则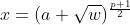 为
为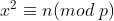 注意
注意 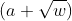 这里的为数域扩张 类似于模意义下的虚数 要重定义运算法则
这里的为数域扩张 类似于模意义下的虚数 要重定义运算法则
证明:




























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








