Implement pow(double x, int n). – leetcode
自定义实现pow函数.
注意点:
(1) double类型的值,不能用 == 来判断是否相等,应该用一定的误差值来判断;
(2) 特殊情况的处理:
1) x 为 0 同时 n 为 0
2) x 不为 0 , n 为 0
3) x 不为 0, n 为 负数的情况.(可以将负数转为正数,然后求结果的倒数. 注意点是:负数的最小值,转为正数的话,就会越界. 解决办法是先对负数加1后,在转为正数,然后乘以1/x, 保证结果).
如果直接用循环迭代的过程求解的话, 时间复杂度过高, 难以通过编译. 观察可以知道:
当n > 0时:
根据迭代公式-有代码:
public:
double Power(double base, int exponent) {
//底数指数均为0, equal(base,0)为判断 base 与 0 是否相等(特殊情况的处理, 这里当底数指数均为 0 的情况下, 值为 1)
if (equal(base,0) && exponent == 0) return 1.0;
//指数为0
if (exponent == 0) return 1.0;
//指数为复数
if (exponent < 0){//指数为负数, 指数加1, 然后转换为正数求解
return 1/base * PowerWithExponent(1/base, -(exponent+1));
}
//指数为正数
return PowerWithExponent(base, exponent);
}
//递归求解想:
//a^x = (1) a^(x/2) * a^(x/2) x为偶数
// (2) a^((x-1)/2) * a^((x-1)/2) * a x为奇数
double PowerWithExponent(double base, int exponent){
//指数为 0, 返回 1
if (exponent == 0) return 1;
//指数为 1, 返回 base
if (exponent == 1) return base;
double result = PowerWithExponent(base, exponent >> 1);//exponent >> 1 位移操作,相当于除以2,但是性能更好
result *= result;
if (exponent & 0x1 ){//exponent & 0x1 相当于求%运算,性能更优. exponent & 0x1 == 1 表示奇数
result *= base;
}
return result;
}
//判断两个double是否相等, 不能用 == 求解
bool equal (double a, double b){
if ((a-b > -0.0000001) && (a-b)<0.0000001) return true;
else return false;
}
};










 本文介绍了一种自定义实现pow函数的方法,通过递归求解并处理特殊情况,如底数和指数为0、指数为负数等。文章还提供了一个高效的解决方案,避免了循环迭代过程中的高时间复杂度。
本文介绍了一种自定义实现pow函数的方法,通过递归求解并处理特殊情况,如底数和指数为0、指数为负数等。文章还提供了一个高效的解决方案,避免了循环迭代过程中的高时间复杂度。
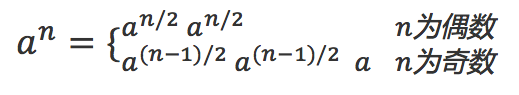
















 514
514

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








