#10002 「一本通 1.1 例 3」喷水装置

最新推荐文章于 2024-12-23 11:15:00 发布

Andy_Xie007

最新推荐文章于 2024-12-23 11:15:00 发布

阅读量585

点赞数 2

分类专栏：贪心算法文章标签：算法数据结构

本文链接：https://blog.csdn.net/Andy_Xie007/article/details/133924582

版权

贪心算法专栏收录该内容

6 篇文章

订阅专栏

文章讲述了在一个二维平面上如何通过最优子结构和勾股定理，确定最少数量的圆来完全覆盖矩形区域，同时满足相邻圆相交的条件，以及如何处理边界情况和提高算法效率的过程。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

解题思路

最优子结构

我们知道，在一个平面上两个圆的位置关系有3种：相交，相切，相离。而对于这道题而言，如果最后喷头能够覆盖题设面积且喷头个数最小，则任意相邻的两个圆必定相交。同时，考虑到必须完整地覆盖到矩形边框，根据勾股定理，两个相邻圆应该满足下列关系：

$(r{_{1}}^{2}-(\frac{1}{2}w)^{2})^{\frac{1}{2}} + (r{_{2}}^{2}-(\frac{1}{2}w)^{2})^{\frac{1}{2}} \geq x_{2} - x_{1}$

下图是一个恰好覆盖的取等临界情况：

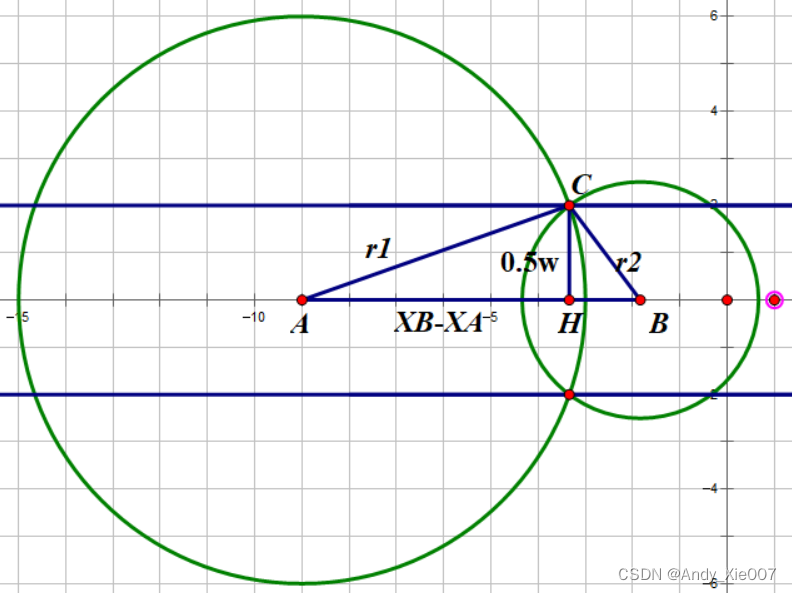
由于每个圆的位置和半径不相关，要想两个相邻圆覆盖面积最大的局部最优解，应当从最右端的圆开始，向左依次判断是否满足上述不等关系。因此有关键步骤如下：

1.对所有圆按照坐标大小从小到大排序。

2.选取左端点圆：从最右圆依次向左遍历（如果向右遍历不能保证找到的是最优解），直到找到最优解，如果没找到，输出-1。

3.选取右端点圆：从最右圆依次向左遍历，直到符合不等关系，更新圆的个数，更新左端点，更新覆盖面积大小，如果达到标准面积则退出循环输出答案；如果没有找到符合题意的圆，输出-1。

边界判断与优化

如果仅完成了上述步骤，那么很可能因为超时和未考虑边界情况而和答主首次提交一样只拿67分。

首先是比较容易想到的优化。如果对两个圆是否覆盖全部矩形面积都使用上述不等式判断，显然不是一个高效率的做法。容易想到，对于一下两种情况，可以直接判否：

1.右端点圆半径小于等于0.5w。（可以直接在排序的时候就筛选出去）

2.左右圆心距离大于等于两圆半径之和。（违反三角形成立的充要条件两边之和大于第三边）

关于第一点的详细证明如下：

1）r < 0.5w; 该范围不在不等式 $(r{_{2}}^{2}-(\frac{1}{2}w)^{2})^{\frac{1}{2}}$ 的定义域内，直接判否。

2）r = 0.5w; 则原不等式退化为 $(r{_{1}}^{2}-(\frac{1}{2}w)^{2})^{\frac{1}{2}} \geq x_{2} - x_{1}$ ，两圆交点（若存在）必然在题设矩形边框上，则容易证明存在圆0满足 $(r{_{0}}^{2}-(\frac{1}{2}w)^{2})^{\frac{1}{2}}\geq x_{1} - x_{0}$ ，使得 $(r{_{0}}^{2}-(\frac{1}{2}w)^{2})^{\frac{1}{2}} + (r{_{2}}^{2}-(\frac{1}{2}w)^{2})^{\frac{1}{2}} \geq x_{2} - x_{0}$ ，即圆0与圆2相交且覆盖相应区域内的全部矩形边框，那么圆1存在与否不影响对矩形的覆盖，可以弃选，相当于不合法判否数据。

应用后的判断函数如下：

bool check(info* left, info* right, const double& w_)
{
    if(left->r + right->r <= right->x-left->x) //第三边和大于两边和
        return 0;
    if(right->r <= w_)   //右端点圆半径小于0.5w
        return 0;
    if(sqrt(left->r*left->r-w_*w_)+sqrt(right->r*right->r-w_*w_) >= right->x-left->x)
        return 1;
    return 0;
}

而所谓的边界判定，就是处理极端数据，如以下两种：

1.找不到覆盖矩形左侧的左端点圆（那么直接输出-1，之前已经处理过了）

2.找到的左端点圆能够覆盖整个矩形，不需要再找右端点圆，直接输出1（比较难想）

int cont = 1;
if((temp_l->r)*(temp_l->r)- w_*w_ >= (l-temp_l->x)*(l-temp_l->x))
   goto ends;          //boundary check!!!

完整代码

#include <iostream>
#include <algorithm>
#include <cmath>

using namespace std;

struct info
{
    double x;
    double r;
};

bool cmp(const info& a, const info& b)
{
    return(a.x < b.x);
}

bool check(info* left, info* right, const double& w_)
{
    if(left->r + right->r <= right->x - left->x)
        return 0;
    if(right->r <= w_)
        return 0;
    if(sqrt(left->r*left->r-w_*w_)+sqrt(right->r*right->r-w_*w_) >= right->x-left->x)
        return 1;
    return 0;
}

info sprayer[15005];

int main()
{
    int g,n;
    double l,w;
    cin >> g;
    for(int i = 0; i < g; i++)
    {
        cin >> n >> l >> w;
        double w_ = w/2;

        for(int j = 0; j < n; j++)
            scanf("%lf %lf", &sprayer[j].x, &sprayer[j].r);

        sort(sprayer, sprayer+n, cmp);

        int cont = 1;
        info* temp_l;
        for(info* start = sprayer+n-1; start >= sprayer; start--)
        {
            if((start->r)*(start->r)-(start->x)*(start->x)>=w_*w_)
            {
                temp_l = start;
                break;
            }
            if(start == sprayer)
            {
                cont = -1;
                goto ends;
            }
        }

        if((temp_l->r)*(temp_l->r)- w_*w_ >= (l-temp_l->x)*(l-temp_l->x))
            goto ends;
        for(; temp_l < sprayer+n-1;)
        {
            for(info* temp_r = sprayer+n-1; ; temp_r--)
            {
                if(temp_l == temp_r)       
                {
                    cont = -1;
                    goto ends;
                }
                if(check(temp_l, temp_r, w_) == 1)
                {
                    temp_l = temp_r;
                    cont++;
                    break;
                }
            }
            if((temp_l->r)*(temp_l->r)- w_*w_ >= (l-temp_l->x)*(l-temp_l->x))
                break;
        }
ends:
        cout << cont << endl;
    }
    return 0;
}