零知识证明中的sigma协议

前置知识

群

令$G$为一个非空集合，$\bullet$是$G$上的一个二元运算，这意味着对于任意的两个$a,b\in G$，都有$a\bullet b\in G$
例子：

$G=Z_{14}=0,1,2,3,4,5,6,7,8,9,10,11,12,13$ "$\bullet$"是模14下的加法
$4\bullet 12=4+12mod14=2$
$G=Z_{14}^{\ast }=1,3,5,9,11,13$ $"\bullet "$是模14下的乘法
$5\bullet 9=5\times 9mod14=3$
$G$如果满足以下性质，则$G$是一个群

1. 封闭性：$\forall a,b\in G,a\cdot b\in G$
2. 关联性：$\exists$元素$1\in G$ 满足$1\cdot a$ =$a\cdot 1$ 对所有的 $a\in G$
3. 可逆性：$\forall a\in G,\exists 一个唯一的b\in G$
   满足$a\cdot b$ = $b\cdot a$ =1;b是a的逆元，记为$a^{-1}$

群的阶

一个群的阶是这个群的大小，也就是群中含有的元素个数
记$G$为阶为$m$的群，则$a^m=1$
对于任意的$i\in Z,a^i=a^{imodm}$
代表元：

生成元与循环群

交互式证明(Interactive Proofs)

一个交互式证明系统包含两方：证明者(Prover)和验证者(Verifier)。给一个陈述，验证方会对证明方提出询问，经过几轮交互之后决定是否这个陈述是真的。直观上说，一个像这样的证明系统满足两个性质：
1、完备性：所有真的陈述都必须有证明。也就是说，经过验证方和证明方的交互后，验证方有能力得出陈述为真的结论。
2、健全性：所有假的陈述都没有证明，恶意的证明者不能说服验证者假的陈述为真。

进入正题

令$p$ 为一个素数，$q|p-1$，且$g$是$Z_p^{\ast }$中阶为$q$的生成元。假设一个证明者(prover)$P$在$Z_q$中随机选择了一个$w$，并且发布了$h=g^{w}modp$。一个验证者(Verifier)V得到了$p,q,g,h$能够检查$p,q$是否为素数，以及$g,h$是否拥有阶$q$。因为在$Z_q^{\ast }$下只有一个阶为$q$的子群，所以$h\in <g>$，存在$w$使得$h=g^w$，但这不代表$P$知道$w$.

Schnorr协议

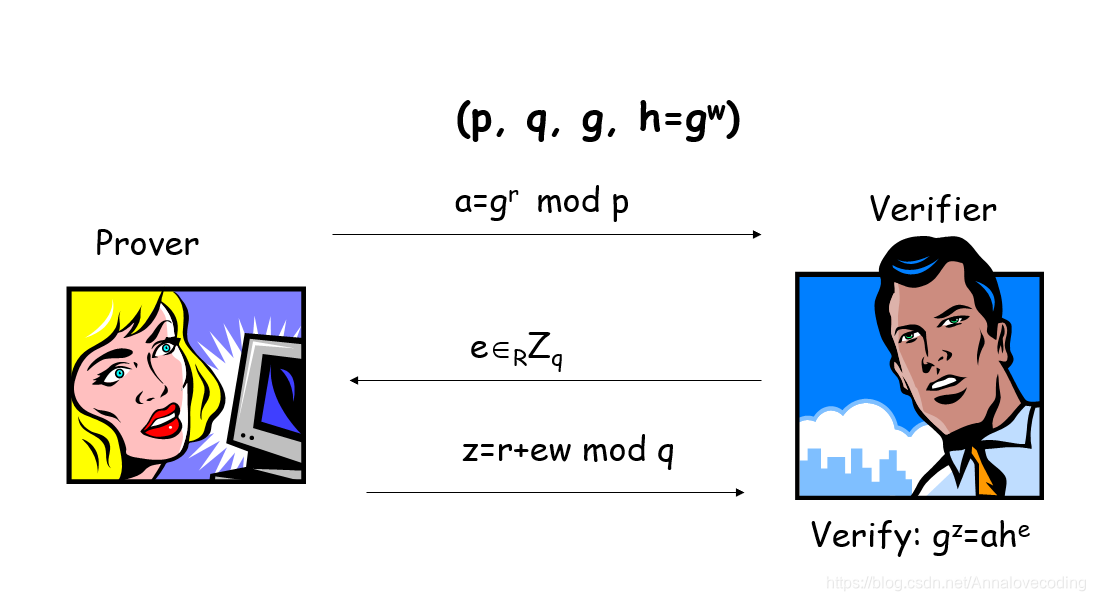
1、$P$随机在$Z_q$中选择一个$r$，将$a=g^{r}modp$送给$V$
2、$V$选择随机一个在$Z_{2^t}$中的挑战信息$e$送给$P$。这里$t$的范围固定为$2^t<q$
3、$P$将$z=r+ewmodq$送给$V$，$V$检查$g^z=a{h}^{e}modp$，如果是则接受

一个恶意的证明者$P$如果不能得到$w$的值，则$P$一次最多只能正确获得一个挑战信息$e$

证明
假如某一证明者$P^{\ast }$，发送$a$，能够正确得到两个不同的挑战信息$e$,$e^{\prime }$。这意味着他可以产生$z,z^{\prime }$同时满足，$g^z=a{h}^{e}modp$和$g^{z^{\prime }}=a{h}^{e^{\prime }}modp$。两个等式两边相除，我们可以得到$h=g^{(}z-z^{\prime })(e-e^{\prime }{)}^{-1}modp$,则$w=(z-z^{\prime })(e-e^{\prime }{)}^{-1}modq$,那么$P^{\ast }$就get到了$w$。

注：恶意的$P$可以先通过计算$a$，然后再通过等式$g^z=a{h}^e$计算$z$的值，因为恶意$P$不知道$w$的值，也可以自己随便选一个$z$

解释：因为如果$e-e^{\prime }\ne 0modq$，恶意证明者就可以获取$w$，反之如果$e-e^{\prime }=0$，则不能获取$w$，不能获取的概率为$1/2^t$（挑战信息$e$的长度为$t$）

$\Sigma$协议