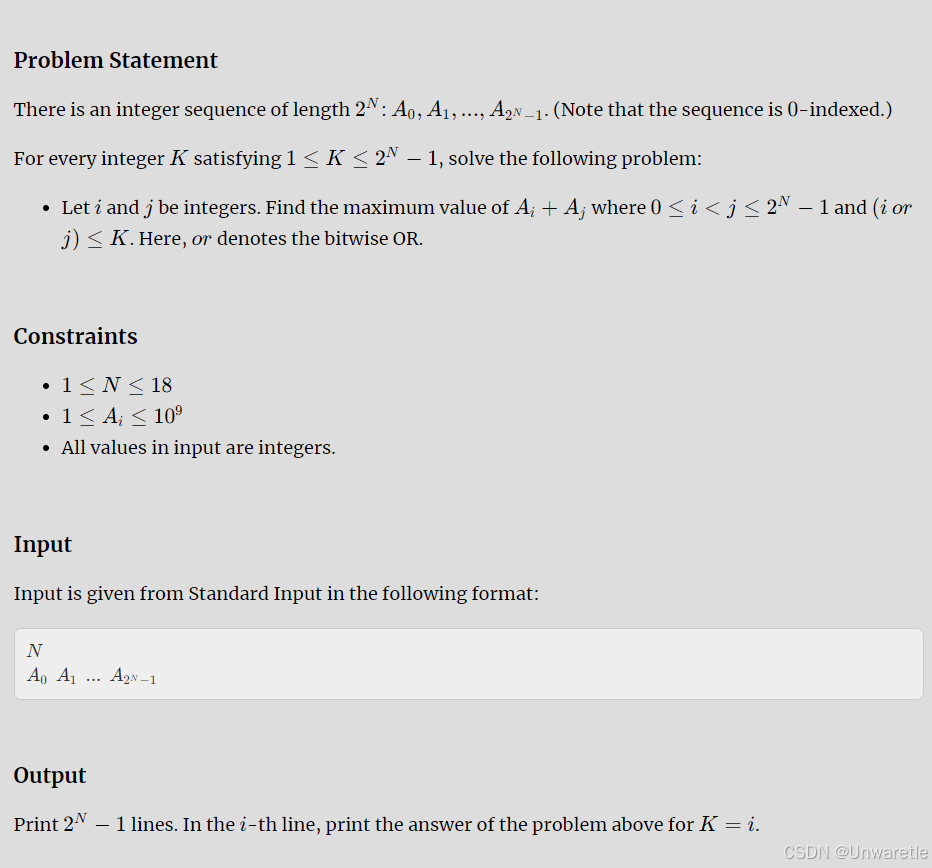
AT_arc100_c [ARC100E] Or Plus Max 高维前缀和（sosdp）

题目大意

给定一个长度为 $2^{n}$ ，起始下标为 0 的数组A，求出满足 i | j <= k（ $k\varepsilon [1,2^{n}]$ ）的前提下， $A_{i}+A_{j}$ 的最大值。

题目分析

看到题目，第一个想法就是，暴力枚举出每一种可能性，然后输出最大值，时间复杂度为O( $2^{2n}$ )，代码如下：

#include <iostream>
using namespace std;
int n, a[(1 << 18)], ans[(1 << 18)] = {};
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    cin >> n;
    for (int i = 0; i < (1 << n); i++) {
        cin >> a[i];
    }
    for (int i = 0; i < (1 << n); i++) {//遍历所有可能性
        for (int j = i + 1; j < (1 << n); j++) {
            ans[i | j] = max(ans[i | j], a[i] + a[j]);
        }
    }
    for (int i = 1; i < (1 << n); i++) {
        ans[i] = max(ans[i], ans[i - 1]);//因为是i|j<=k，所以当前结果应该为前k个的最大值
        cout << ans[i] << "\n";
    }
}

显然，时间复杂度太高，TLE了。

那么，有没有更快速的方法呢？

不妨换个思路，在一堆数中找到两个数使得二者的和为最大值的充要条件是这两个数为这一堆数中的最大值和次大值。那么，求第K项的 $A_{i}+A_{j}$ 的最大值（i | j = k），只要找出所有满足下标能与任意数取或后等于k的数的最大值和次大值即可。

根据或的性质，有：

0 | 0 = 0 1 | 0 = 1 1 | 1 = 1

所以，在二进制的情况下，如果 i 能与任意数取或后等于 k ，则当 k 的第 j 位为 0 时，i 的第 j 位必为 0；当 k 的第 j 位为 1 时，i 的第 j 位可为 0 或 1。换而言之，对于数 k，如果k的第 j 位为1，则（k ^ (1 << j )）必然满足与某个数取或后等于 k 。

上述情况，必然不一定为能与任意数取或后等于 k 的所有情况，但是，如果我们从前往后，维护一个前缀数组，就可以保证遍历所有的情况了，即维护一个高维前缀和。（其实这题就是高维前缀和的模板题）

代码实现

#include <iostream>
using namespace std;
long long n, first[(1 << 18)] = {}, second[(1 << 18)] = {}, ans = 0;
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    cin >> n;
    for (int i = 0; i < (1 << n); i++) {
        cin >> first[i];//将第i位的最大值初始化为A[i]，次大值初始化为0
        second[i] = 0;
    }
    for (int j = 0; j < n; j++) {//判断位数
        for (int i = 0; i < (1 << n); i++) {//遍历每一种可能
            if ((i >> j) & 1) {//二进制下第j位为1，找到 i^(1 << j)，更新第i位的最大值和次大值
                if (first[i] > first[i ^ (1 << j)]) {
                    second[i] = max(second[i], first[i ^ (1 << j)]);
                }
                else {
                    second[i] = max(second[i ^ (1 << j)], first[i]);
                    first[i] = first[i ^ (1 << j)];
                }
            }
        }
    }
    for (int i = 1; i < (1 << n); i++) {
        ans = max(ans, first[i] + second[i]);
        cout << ans << "\n";
    }
}