探秘量子电路——量子计算中的数字电路

1. 引言

在2025年的 IBM Qiskit Fall Fest 活动中，有展示一张量子电路的示意图，其与下图类似，但抽象程度更低。

量子电路 是量子计算中与 数字电路 对应的概念，而数字电路是所有计算机的基础。与数字电路图类似，量子电路图是对可以在量子计算机上运行的算法底层逻辑和操作的可视化表示。

本文将对量子电路与数字电路进行比较和对照，并通过简单、实用的量子计算示例，解释如何创建量子电路图。

2. 数字电路 vs. 量子电路

量子电路是量子计算中对应于日常经典计算里的数字电路的概念。它们之所以相似，是因为彼此在各自体系中扮演着等价的角色。然而，由于经典计算与量子计算在本质上存在巨大差异，这两种电路也有着明显的不同。

下面的示意图对比了数字电路和量子电路，展示了它们在图形表示上的相似之处以及各自独特的组成部分。

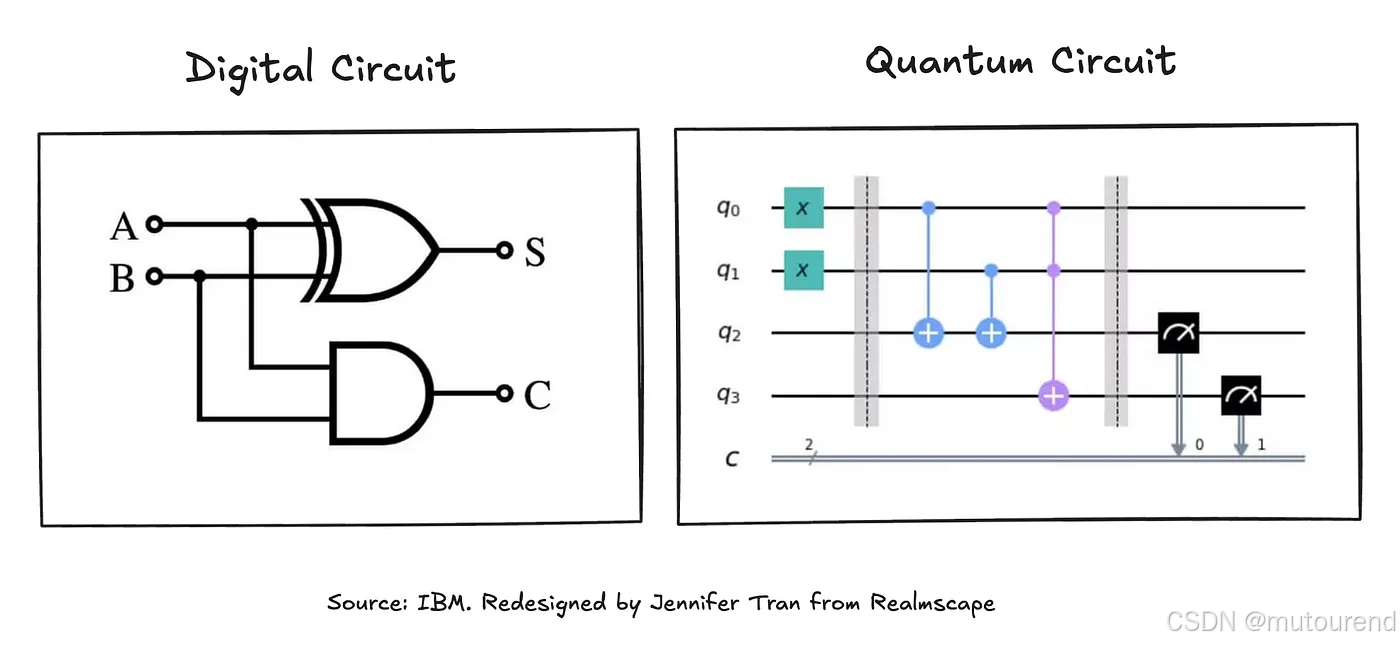
上图左侧为经典数字电路，右侧为量子电路，二者在图形上具有相似性，但组成部件各不相同。源自：IBM

2.1 数字电路

数字电路构成了经典计算机的基本基础。

一台典型的计算机中包含数百万，甚至数十亿个数字电路，每个电路执行简单的逻辑运算，这些运算叠加在一起，形成复杂的计算和任务。多层电路在需要高可靠性和高复杂度的设备中非常常见，如医疗仪器和高性能计算机，每一层都包含成千上万个独立电路。

下图为一个计算机电路板的示例，可能由成千上万甚至数百万个数字电路组成。图片源自：GlobalWellPCBA

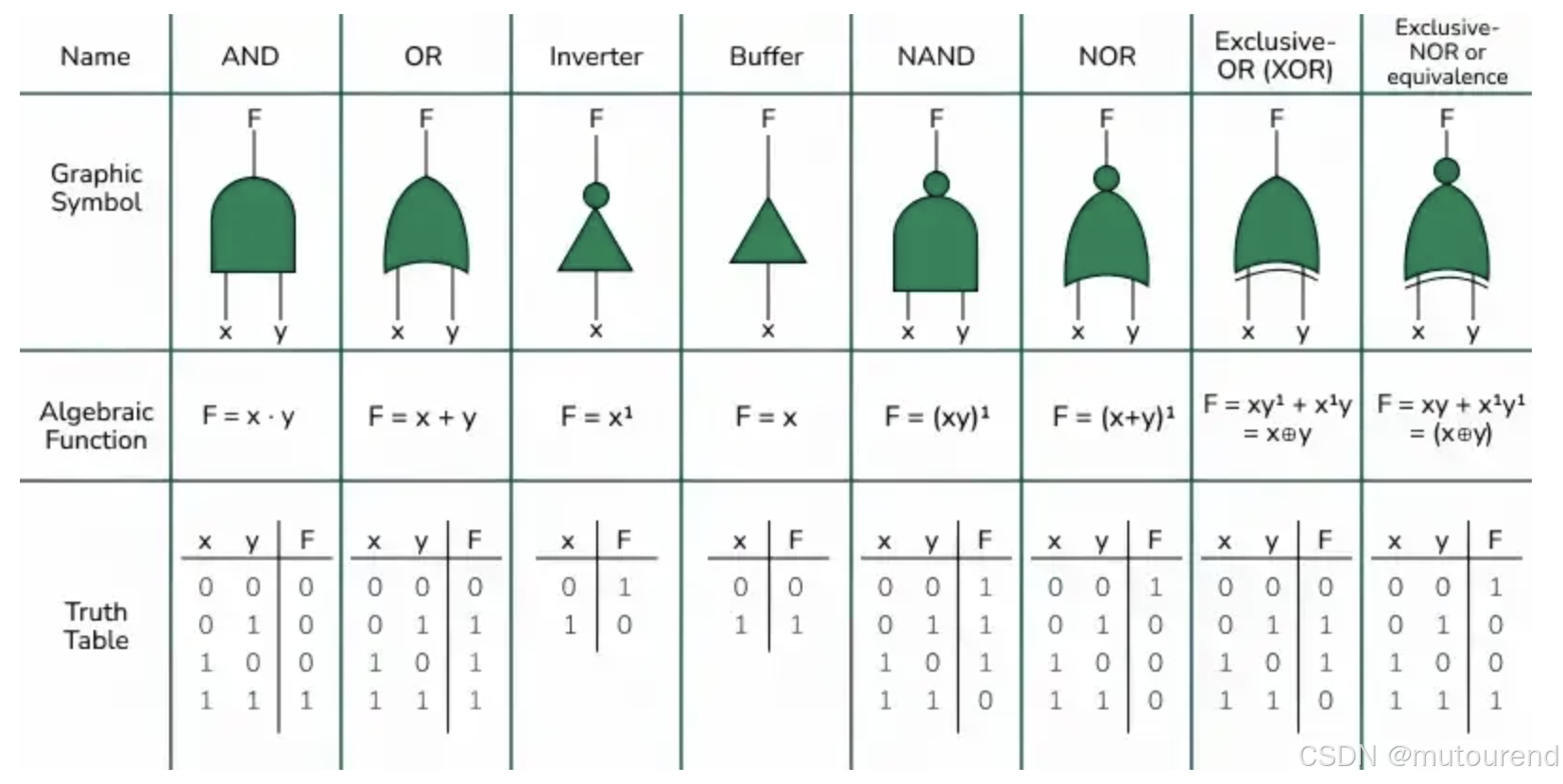
一个单独的数字电路通过称为逻辑门的小型组件来处理简单规则，逻辑门负责执行逻辑运算（AND、OR、NOT）。

下图这个简单的 AND 逻辑门展示了两个输入（A 和 B）如何产生一个组合输出（Y）。在二进制中，当 A 和/或 B 为 0 时，Y 为 0。只有当 A 和 B 都为 1 时，Y 才会为 1。

上图源自：Renesas

在更实际的层面上，下面这个示例展示了一个包含 AND 门的数字电路，如何基于上述二进制示例来控制 LED Y 的亮灭。当输出 Y 中的开关 SW A 和/或 SW B 关闭（即为 0）时，LED Y 熄灭（或为 0）。当 SW A 和 SW B 都打开（即为 1）时，LED Y 点亮（或为 1）。

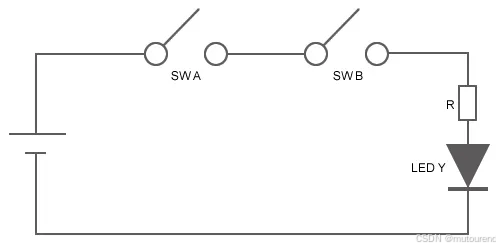
上图展示了 LED Y 如何由开关 SW A 和 SW B 控制。图片源自：Renesas

单个电路可以执行基本操作，如一个简单的电灯开关；但要完成复杂且有意义的任务，则需要大量这样的电路，这正是计算机的设计初衷。所提供的 Raspberry Pi（一种带触摸屏的小型、低成本单板计算机）的电路图，展示了其相对于电灯开关示例而言要复杂得多。

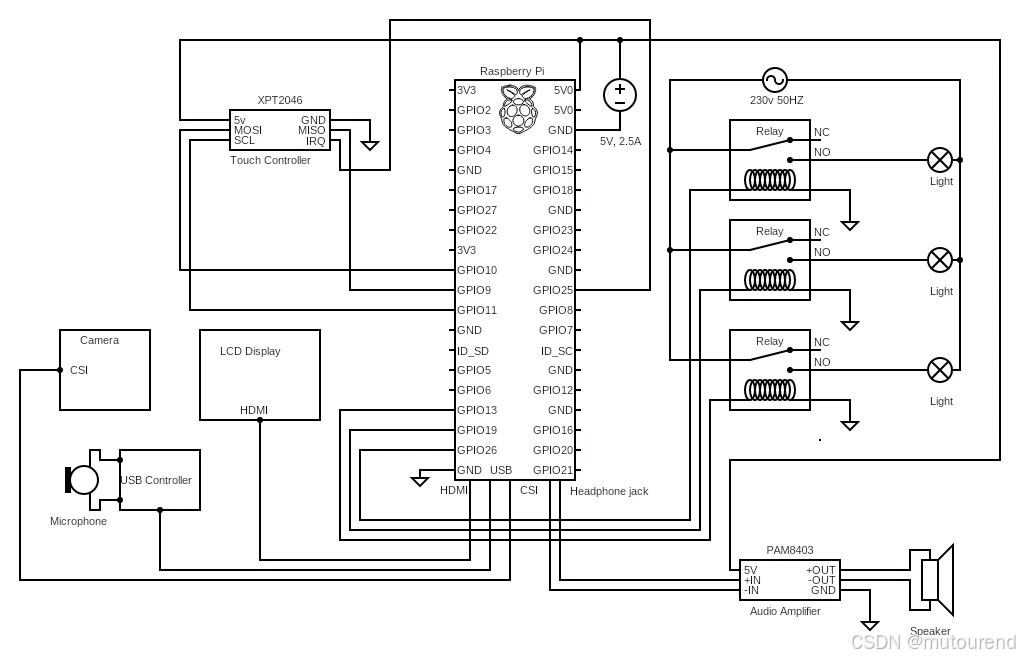
上图为一个带触摸屏的 Raspberry Pi 的数字电路示例。图片源自：Shelin Vankawala

2.2 量子电路

正如数字电路构成了经典计算机的基础一样，量子电路则是量子计算机的基础。

2.2.1 量子电路的规模

完成复杂的量子计算任务所需的量子电路数量更少，因为量子电路相较于数字电路具有更强的计算能力。

一个量子计算机由几十个或几千个量子电路组成，远少于运行一台日常计算机所需的数百万个电路。根据 IBM 和 Google 的说法，100 个 量子比特（qubit）——量子计算中的基本信息单元——是运行小规模科学研究实验算法的一个基准。目前最大的量子计算机拥有 6,100 个量子比特。东京大学、芝加哥大学以及 IBM 的研究人员已承诺在 2033 年前开发一个 10 万量子比特系统，这将使诸如医学建模和农业研究等目前尚无法解决的实际应用成为可能。

2.2.2 量子电路的技术架构

与数字电路中由单个电路的逻辑组合形成复杂操作类似，量子电路定义了量子计算机所执行的计算过程。

量子计算机由量子处理单元（QPU）组成，而 QPU 是由量子电路构成的。量子电路由一个量子比特寄存器组成，每个量子比特都通过执行逻辑运算的量子门进行操作。

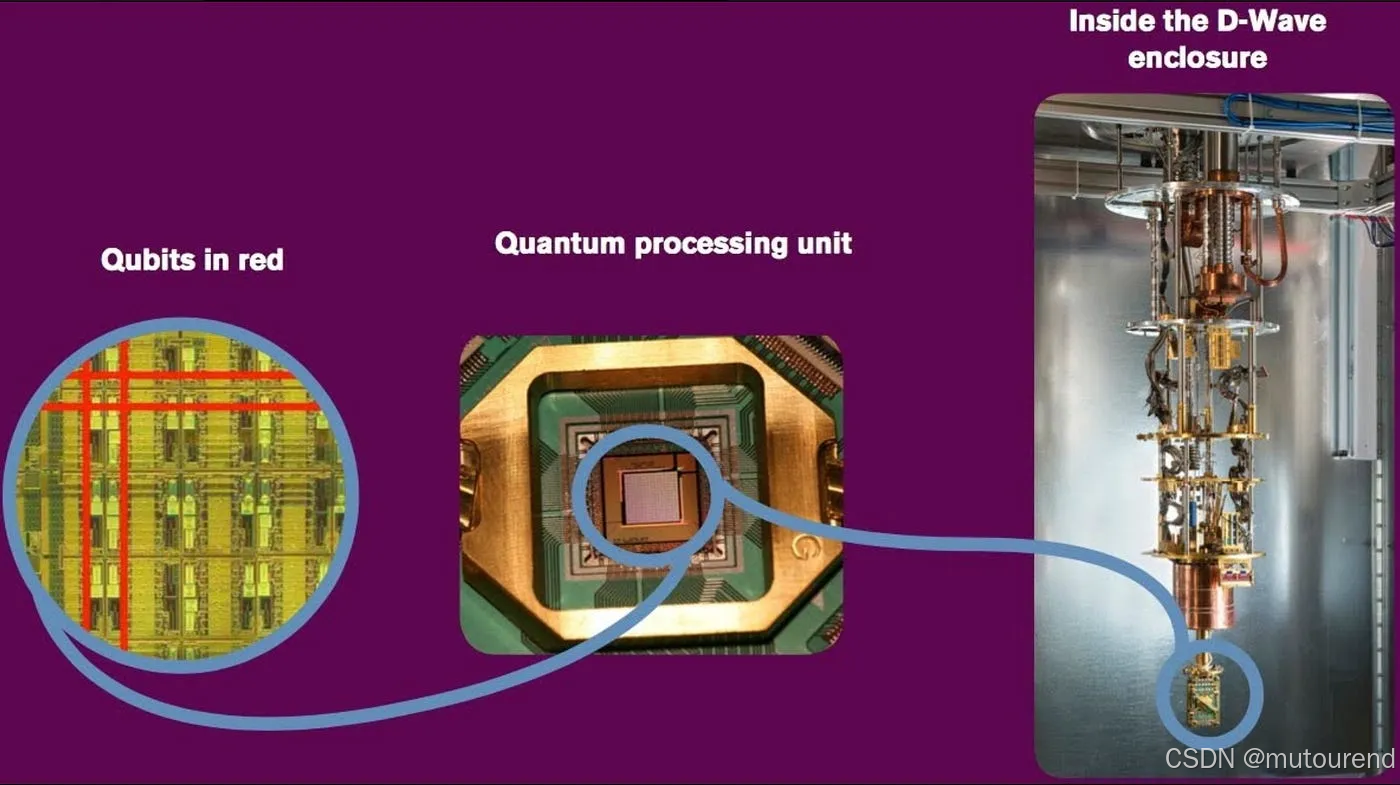上图展示了位于 D-Wave 外壳内部的量子处理单元中的量子比特，该外壳是量子计算机中的一个“黑盒”。源自：Nvidia

量子电路同样使用经典组件。当状态发生变化时，测量结果会存储在量子电路中的经典比特中。这通常在量子电路图中通过一条标记为 “c4” 的线来表示。

下图是一个已初始化的量子电路示例，它包含一个由四个量子比特（q[0]、q[1]、q[2]、q[3]、q[4]）组成的寄存器，以及一个经典寄存器（c4）：

与数字电路类似，量子门执行逻辑运算并改变电路的状态。然而，量子电路中的量子门与数字电路中的逻辑门不同，因为与经典比特不同，量子比特可以同时处于 0 和 1 的状态，而且量子计算必须是可逆的，即输入必须能够被重构。

量子计算必须是可逆的，这是由量子力学原理决定的。量子态包含整个量子系统所有可能的测量结果，其总概率始终为 1，并且在系统演化过程中必须保持这一性质。为了确保所有测量结果的概率之和为 1，量子门必须以一种保留全部信息的方式来变换状态。如果在计算过程中信息发生丢失，某些结果可能会重复出现，导致所有量子态上的总概率无法形成一个正确的概率分布，从而使总概率不再等于 1 。

因此，量子门不能与经典逻辑门相同，因为经典输入可以根据其输出被识别或重构。一个很好的例子是前面解释过的电灯开关场景。当灯是关着的时候，无法确定它是因为 SW A 和 SW B 都关闭了，还是因为只有其中一个开关关闭了。

量子门的种类数量远多于八种经典逻辑门，因此，与其逐个解释它们，不如通过应用电路示例来说明其中的一些量子门更有价值。

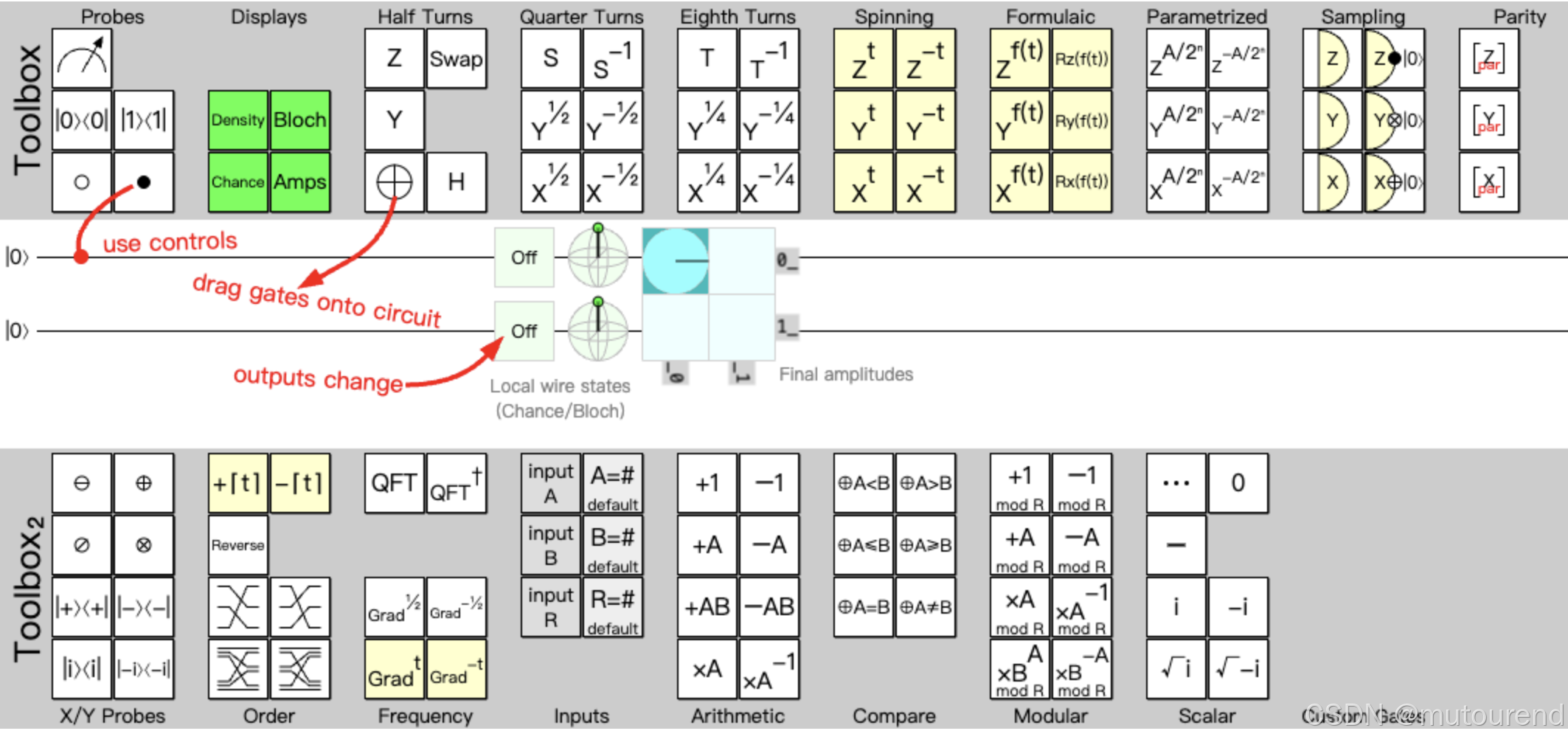
2.2.3 量子电路示例

将使用 IBM Quantum Platform Circuit Composer 作为绘图工具，通过一些适合初学者的量子电路示例来解释电路组件。除此之外，还有许多用于创建量子电路图的工具，如 Quirk、QuantumJS 以及斯图加特大学（University of Stuttgart）提供的工具。

2.2.3.1 最简单的示例

最简单的量子电路示例由一个改变量子态的单一量子门组成。下面的示例演示了如何初始化一个量子比特并使其准备就绪。

量子比特可以处于 |0⟩ 或 |1⟩ 状态。最初，量子比特处于基态 |0⟩。要初始化一个量子比特，必须将其从基态移动到 |1⟩ 状态。其中一种方法是施加一个 NOT 门，它会对状态进行取反（切换到相反的状态）。下图这个量子电路（q[0]）只有一个 NOT 门（用一个圆形目标符号表示），并且该门作用于一个量子比特：

2.2.3.2 稍微复杂一些的示例

另一个更复杂、但仍然相对简单的示例是一个展示两个量子比特之间量子纠缠的电路。量子纠缠是指量子比特彼此连接并产生相关性，即使它们后来被相隔很远，这种关联仍然存在。量子纠缠正是使量子计算能够同时处理多个量子比特、从而具备高速和强大计算能力的现象。

如前所述，量子比特从基态 |0⟩ 开始。通过施加一个 Hadamard 门（在电路图中表示为一个带有字母 H 的方框），量子比特可以同时处于 |0⟩ 和 |1⟩ 的叠加态。

如，下图展示了量子比特（q[0]）处于 |0⟩ 和 |1⟩ 的叠加态：

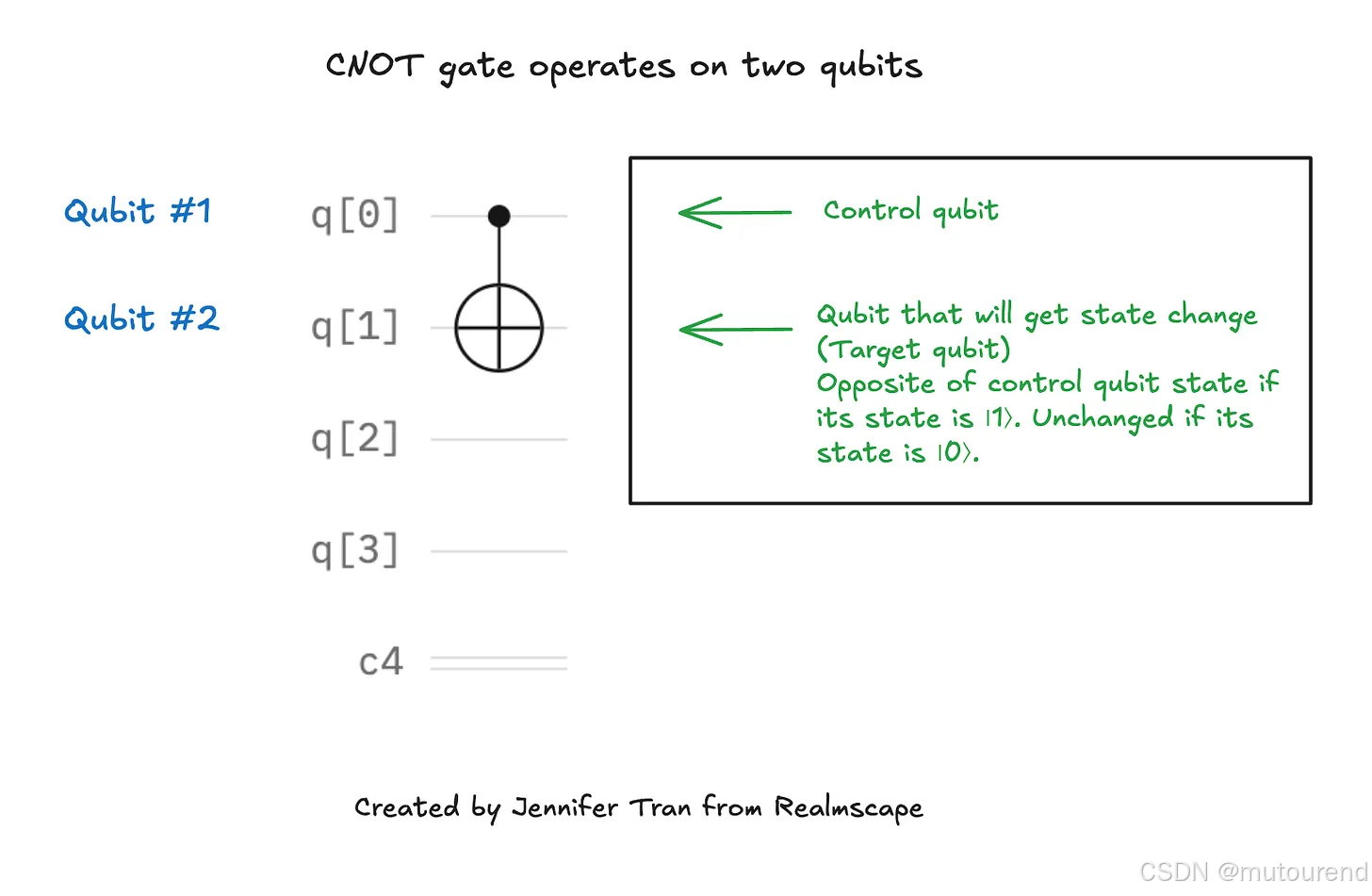
要与另一个量子比特建立连接或形成纠缠，电路需要施加一个同时作用于两个量子比特的双量子比特组件。受控非门（controlled NOT，或 CNOT 门）需要两个量子比特：第一个是控制量子比特，第二个是目标量子比特；只有当控制量子比特的状态为 |1⟩ 时，它才会将目标（第二个）量子比特的状态翻转为与控制量子比特状态相反的状态。
下图说明 CNOT 门如何一次同时作用于两个量子比特：

接下来的电路示例展示了两个发生纠缠、或具有“相互连接”状态的量子比特。第一个量子比特（q[0]）由于施加了 Hadamard 门而处于叠加态，同时包含 |0⟩ 和 |1⟩ 两种状态。第二个量子比特（q[1]）在 CNOT 门的作用下，通常期望处于第一个量子比特的相反状态，其中第一个量子比特是控制位，第二个量子比特是目标位。然而，由于叠加态并不存在一个确定的“相反”状态，第二个量子比特的最终状态取决于第一个量子比特状态的测量结果。

下图为一个包含 Hadamard 门和 CNOT 门的双量子比特示例，这两个量子比特彼此纠缠：

2.2.3.3 算法示例

与经典计算类似，量子电路在实现复杂算法时需要更多资源，通常涉及多个量子比特和多个量子门。

Deutsch 算法 是最早证明量子计算机在某些问题上比经典计算机更强大的量子算法之一。

一个未知函数 f(x) 只接受 0 或 1 作为输入。它有两种可能：

• 常数型（始终返回 0 或始终返回 1）：如果输入 0 和 1 得到的输出完全相同（始终为 0 或始终为 1），则该函数被认为是常数型
• 或 平衡型（在 0 和 1 之间变化）：如果输出不同（一个为 0，另一个为 1），则该函数被认为是平衡型。

换句话说（详情参见2024年博客 Step by step guide to Deutsch’s Algorithm）：

如果在输入 0 或 1 时得到以下结果，那么该函数是常数型：

f(0)=0 且 f(1)=0，则 f(x) 为常数（始终为 0）
f(0)=1 且 f(1)=1，则 f(x) 为常数（始终为 1）

如果在输入 0 或 1 时得到以下结果，那么该函数是平衡型：

f(0)=0 且 f(1)=1，则 f(x) 为平衡型（0 与 1 各一次）
f(0)=1 且 f(1)=0，则 f(x) 为平衡型（0 与 1 各一次）

要判断函数f是常数型还是平衡性？

• 在经典计算中，需要调用该函数两次：一次输入 0，一次输入 1。
• Deutsch 利用量子计算提出了一种更高效的方法：通过同时将 0 和 1 输入到两个量子比特中，只需调用一次函数即可完成判断。

下面的示例展示了 Deutsch 算法。该示例被划分为五个关键步骤，并在下文中用通俗的语言加以说明。如果想理解该算法背后的数学原理，可以参看2023年视频Deutsch’s Algorithm: An Introduction to Quantum Computing Oracles；如果希望查看或复现 Qiskit 代码，可以参考这个教程。

其中：

• 1）步骤一 —— 初始化
  首先，需要两个彼此独立的量子比特：一个用于测试函数，另一个用于处理输出结果的最终测量（即判断函数是平衡型还是常数型）。
  第一步是准备两个量子比特：

  • 用于测试函数的量子比特处于基态且未初始化，如 q[0] 所示；
  • 另一个量子比特用于存储输出的测量结果，通过施加一个 NOT 门将其初始化，如 q[1] 所示。

  下图展示了 Deutsch 算法的第一步：从两个量子比特开始，一个处于基态，另一个处于已初始化状态。
  

• 2）步骤二 —— 叠加态
  为了测试该函数，需要传入两个不同的输入。第一个量子比特用于测试函数，通过施加 Hadamard 门，使其进入 |0⟩ 和 |1⟩ 两种状态的叠加态，从而同时接收这两个输入。
  第二个量子比特同样需要施加一个 Hadamard 门，以对最终结果进行编码。
  下图展示了第二步，其中通过 Hadamard 门将两个量子比特都置于叠加态：
  

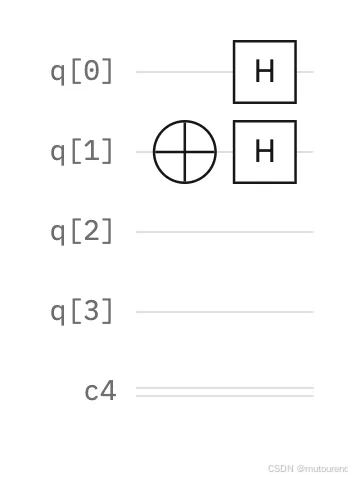
• 3）步骤三 —— 使用函数
  接下来，施加一个概念性的函数（也称为预言机（oracle）或黑盒），它展示了函数如何作用，但并不直接揭示函数的具体形式。
  在电路中，该函数通过 CNOT 门和 NOT 门的不同组合来表示，用以构造前面提到的四种函数可能性：

  f(0)=0 且 f(1)=0，则 f(x) 为常数型（始终为 0）
  f(0)=1 且 f(1)=1，则 f(x) 为常数型（始终为 1）
  f(0)=0 且 f(1)=1，则 f(x) 为平衡型（0 与 1 各一次）
  f(0)=1 且 f(1)=0，则 f(x) 为平衡型（0 与 1 各一次）
  

  每一个“预言机（oracle）”都实现了以下函数之一：

  • 无量子门：函数始终输出 0，第二个量子比特保持不变
  • 仅使用 NOT 门：函数始终输出 1，无论输入为何，都会翻转第二个量子比特
  • 使用 CNOT 门：函数输出与第一个量子比特相同的值（0→0，1→1），形成一个平衡函数
  • 使用 CNOT + NOT 门：函数输出第一个量子比特的相反值（0→1，1→0），形成另一种平衡函数

  下图展示了第三步：需要实现概念性的函数 / 预言机 / 黑盒，以说明这些函数是如何工作的：【虚线仅用于视觉上的分隔与说明，没有任何实际功能。】
  

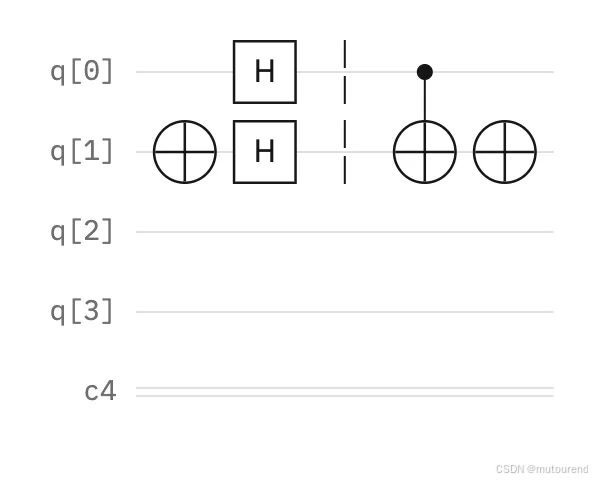
• 4）步骤四 —— 干涉
  接下来，为了测量具体状态，需要让第一个量子比特不再同时处于多个状态。为此，对其施加一个 Hadamard 门，以对其叠加态进行干涉或抵消。
  下图展示了新增的第四步：消除叠加态。
  

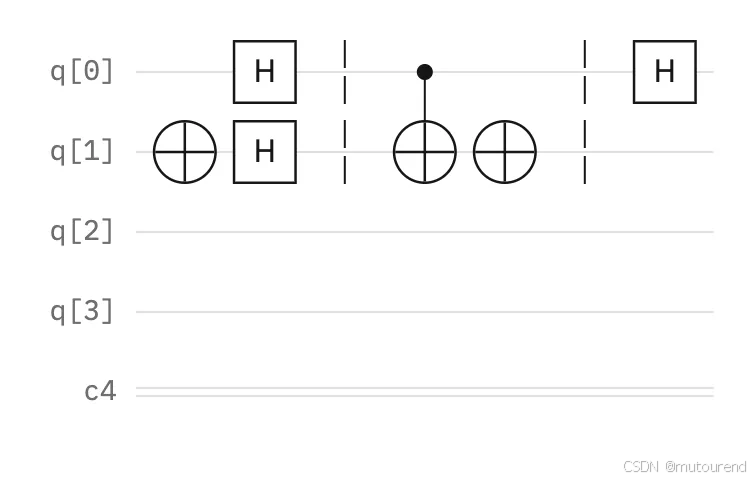
• 5）步骤五 —— 测量
  最后，使用一个测量组件对第一个量子比特进行测量，该组件在电路图中表示为一个带有燃料表样式指示器、并在刻度处标有 “z” 的方框。
  如果函数是常数型，测量结果将始终为 0；如果函数是平衡型，结果将为 1 。经典寄存器（c4）旁的数字表示存储测量结果的比特索引，而不是测量的数值大小。
  在本例中，测量结果为 1，因此可以判断该函数是平衡型。
  下图为最终的电路图，展示了最后一步：对第一个量子比特的最终状态进行测量。
  

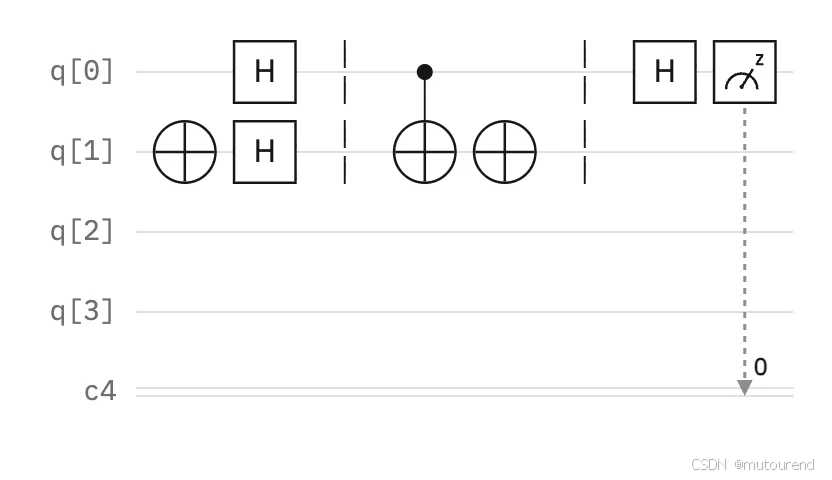
3. 运行电路

当开发者在云环境（如 IBM Quantum Platform）中绘制并运行这样的量子电路图时，云端会解析并解释该电路图，然后将解析结果（即“指令”）发送到受室温控制的电子设备中。这些设备随后产生符合电路图指令的特定信号，并最终传递给量子比特，使其严格按照指令执行操作。

4. 结论

尽管量子电路非常复杂，但学习它们的过程十分引人入胜。量子电路需要大量量子力学方面的知识，即使具备计算机科学背景，也很难完全理解。

虽然从整体上看，量子电路更为强大，且所需数量更少，但它们本身同样具有高度复杂性。尽管与数字电路存在一些共同点，量子电路在本质上仍然与数字电路截然不同。

参考资料

[1] 2025年12月博客 How to create a quantum circuit