LLM - Whitening Sentence Representations for Better Semantics and Faster Retrieval 用于更好语义更快检索的句子白化操作-CSDN博客

BERT 等预训练模型在许多自然语言处理任务中取得了巨大成功。然而，如何通过这些预训练模型获得更好的句子表示仍然值得利用。以前的工作表明，各向异性问题是基于 BERT 的句子表示的一个关键瓶颈，这阻碍了模型充分利用底层语义特征。因此，一些提高句子分布的各向同性的尝试，例如基于流的模型，已应用于句子表示并取得了一些改进。在本文中，我们发现传统机器学习中的白化操作可以类似地增强句子表示的各向同性并实现有竞争力的结果。此外，白化技术还能够降低句子表示的维度。实验结果表明，它不仅可以达到良好的性能，而且显著降低了存储成本，加快了模型检索速度。

1.Introduce

[介绍]

深度神经网络模型的应用近年来取得了巨大的成功，因为它们创建了对周围环境敏感的上下文化词表示。这一趋势还刺激了生成较长文本的语义表示的进步，例如句子和段落。然而，正如之前的工作认为所有单词的单词表示不是各向同性的: 它们相对于方向不是均匀分布的。相反，它们在向量空间中占据一个狭窄的锥，因此是各向异性的。(Ethayarajh, 2019) 已经证明来自预训练模型的上下文词嵌入是如此各向异性，以至于平均而言，任意两个词嵌入的余弦相似度为 0.99。 (Li et al., 2020) 的进一步调查发现 BERT 句子嵌入空间存在两个问题，即词频偏差嵌入空间，低频词稀疏分散，这导致难以通过简单的相似性度量（例如点积或余弦相似度）直接使用 BERT 句子嵌入。

为了解决上述问题，(Ethayarajh, 2019) 详细阐述了导致各向异性问题的理论原因，如预训练模型中观察到的。(Gao et al., 2019) 设计了一种通过正则化词嵌入矩阵来减轻退化问题的新方法。最近一种名为 BERT-flow (Li et al., 2020) 的尝试提出通过归一化流将 BERT 句子嵌入分布转换为平滑和各向同性的高斯分布 (Dinh et al., 2014)，这是一种由神经网络参数化的可逆函数。

在本文中，我们发现一种简单有效的后处理技术-白化-能够足以解决句子嵌入的各向异性问题（Reimers 和 Gurevych，2019 年）。具体来说，我们将句子向量的平均值转换为 0，将协方差矩阵转换为单位矩阵。此外，我们还引入了降维策略来促进白化操作，以进一步提高我们方法的有效性。

7 个标准语义文本相似性基准数据集的实验结果表明，我们的方法通常可以提高模型的性能，并在大多数数据集上实现了最先进的结果。同时，通过添加降维操作，我们的方法可以进一步提高模型的性能，并自然地优化内存存储并加快检索速度。

本文的主要贡献总结如下：

• 我们探索了基于 BERT 的句子嵌入在相似性匹配任务中表现不佳的原因，即它不是在标准正交基中。

• 提出了一种白化后处理方法，将基于 BERT 的句子转换为标准正交基，同时减小其大小。

• 七个语义文本相似性任务的实验结果表明，我们的方法不仅可以显着提高模型性能，还可以减小向量大小。

[相关工作]

解决各向异性问题的早期尝试出现在特定的 NLP 环境中。(Arora et al.， 2017) 首先计算整个语义文本相似度数据集的句子表示，然后从这些句子表示中提取顶部方向，最后将句子表示从其上投影出去。通过这样做，顶部方向将固有地编码整个数据集的公共信息。(Mu 和 Viswanath, 2018) 提出了一种对具有正负条目的密集低维表示的后处理操作，它们从单词向量中消除了共同的平均向量和一些顶部主导方向，从而使现成的表示更加强大。(Gao et al.， 2019) 提出了一种新的正则化方法来解决自然语言生成模型训练中的各向异性问题。他们设计了一种新的方法，通过正则化词嵌入矩阵来缓解退化问题。观察到词嵌入被限制在一个狭窄的锥体中，所提出的方法直接增加锥体孔径的大小，这可以通过降低单个词嵌入之间的相似度来实现。(Ethayarajh, 2019) 研究了语境语境化词语表征的内在机制。他们发现 ELMo、BERT 和 GPT-2 的上层比下层产生更多的上下文特定表征。这种增加的环境特异性总是伴随着增加的各向异性。在 (Ethayarajh, 2019) 的工作之后，(Li et al.， 2020) 提出了BERT-flow，其中通过对无监督目标学习的流进行归一化，将各向异性的句子嵌入分布转换为光滑的各向同性高斯分布。

在最先进的句子嵌入方法方面，以前的工作 (Conneau et al.， 2017; Cer et al.， 2017) 发现 SNLI数据集适合训练句子嵌入，(Yang et al.， 2018) 提出了一种使用 siamese DAN 和 siamese transformer 网络对 Reddit 对话进行训练的方法，在 STS 基准数据集上取得了良好的结果。(Cer et al.， 2018) 提出了一种所谓的通用句子编码器，该编码器训练 transformer 网络，并通过在 SNLI 数据集上的训练来增强无监督学习。在预训练方法的时代，(Humeau等人，2019) 解决了BERT 交叉编码器的运行时开销，并提出了一种方法(多编码器)，利用注意力计算上下文向量和预计算的候选嵌入之间的分数。( Reimers 和 Gurevych, 2019) 是对预训练的 BERT 网络的修改，它使用连体和三重网络结构来获得语义上有意义的句子嵌入，可以使用余弦相似度进行比较。

3.Our Approach

[我们的方法]

3.1 hypothesis

[假设]

句子嵌入应该能够直观地反映句子之间的语义相似度。当我们检索语义相似的句子时，我们通常将原始句子编码成句子 embedding 表示，然后计算其角度的余弦值进行比较或排序 (Rahutomo et al.， 2012)。因此，一个发人深省的问题出现了: 余弦相似性对输入向量做了什么假设? 换句话说，用余弦相似度比较向量的前提条件是什么?

我们通过研究余弦相似度的几何来回答这个问题。几何上，给定两个向量 x ∈ R-d和 y ∈ R-d，我们知道 x 和 y 的内积是欧氏模和它们夹角余弦的乘积。因此，余弦相似度 cos(x, y) 是 x 和 y 的内积除以它们的范数:

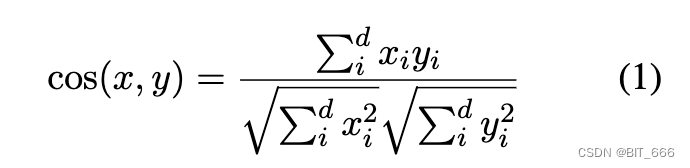
然而，只有当坐标基是标准正交基时，上述方程 1 才得到满足。角度的余弦具有不同的几何含义，但方程 1 是基于不同操作的，这取决于所选择的坐标基。因此，内积的坐标公式随坐标基的变化而变化，余弦值的坐标公式也会相应变化。

(Li et al., 2020) 证实 BERT (Devlin et al., 2019) 的句子嵌入包含了足够的语义，尽管它没有被适当地利用。在这种情况下，如果当对方程 1 进行操作以计算语义相似度的余弦值时句子嵌入表现不佳，原因可能是句子向量所属的坐标基础不是标准正交基。从统计的角度来看，我们可以推断，当我们为一组向量选择基础时，应该确保每个基向量是独立的和统一的。如果这组基础是标准正交基，那么相应的向量集应该显示各向同性。

总而言之，上述启发式假设详细表明：

如果一组向量满足各向同性，我们可以假设它源自标准正交基，其中它还表明我们可以通过等式 1 计算余弦相似度。

否则，如果它是各向同性的，我们需要以强制它是各向同性的方式转换原始句子嵌入，然后使用等式 1 来计算余弦相似度。

3.2 Whitening Transformation

[白化转换]

以前的工作（Li et al., 2020）通过采用基于流的方法解决了第 3.1 节中的假设。我们发现，利用机器学习中常用的白化操作也可以获得可比较的增益。

据我们所知，平均值为 0 的协方差矩阵是关于标准正态分布的单位矩阵。因此，我们的目标是将句子向量的平均值转换为 0，协方差矩阵转换为单位矩阵。据推测，我们有一组句子嵌入，它也可以写成一组行向量 {xi}，然后我们在方程式中进行线性变换，使得 {xi} 的平均值为 0，协方差矩阵为单位矩阵：

上述等式 2 实际上对应于机器学习中的白化操作（Christiansen，2010）。为了使平均值等于 0，我们只需要启用：

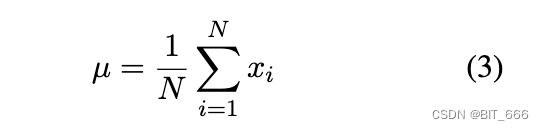
最困难的部分是求解矩阵 W。为此，我们将 {xi} 的原始协方差矩阵表示为：

然后我们可以得到变换后的协方差矩阵̃ Σ:

由于我们指定新的协方差矩阵是一个单位矩阵，我们实际上需要求解下面的等式 6：

因此有:

我们知道协方差矩阵 Σ 是一个正定对称矩阵。正定对称矩阵满足以下形式的 SVD 分解（Golub 和 Reinsch，1971）：

其中 U 是正交矩阵，Λ 是对角矩阵，对角元素都是正数。因此，令:

我们可以得到解决方案：

3.3 Dimensionality Reduction

[降维]

到目前为止，我们已经知道句子嵌入的原始协方差矩阵可以通过利用变换矩阵转换为单位矩阵:

其中，正交矩阵 U 是 distance-preserving 即距离保持变换，这意味着它不会改变整个数据的相对分布，而是将原始协方差矩阵 Σ 转换为对角矩阵 Λ。

据我们所知，对角矩阵 Λ 的每个对角元素都衡量了它所在的一维数据的变化。如果其值很小，则表示该维度特征的变化也很小且不显着，即使在一个常数附近。因此，原始句子向量可能只嵌入到低维空间中，我们可以在操作降维的同时去除这个维度特征，从而使余弦相似度的结果更合理，自然加快了向量检索的速度，因为它与维度成正比。

事实上，从奇异值分解 (Golub and Reinsch, 1971) 导出的对角矩阵 Λ 中的元素已按降序排列。因此，我们只需要保留 W 的前 k 列来实现这种降维效果，这在理论上等同于主成分分析 (Abdi and Williams, 2010)。这里，k 是一个经验超参数。我们将整个转换工作流程称为 Whitening-k，其中详细的算法实现如 Alogrithm-1 所示：

3.4 Complexity Analysis

[复杂性分析]

在语料库大规模的计算效率方面，可以递归计算平均值 μ 和协方差矩阵 Λ。更具体地说，上述所有算法都需要是整个句子向量 {xi} 的平均值向量 μ ∈ R-d 和协方差矩阵 Σ ∈ R-d×d（其中 d 是词嵌入的维度）。因此，给定新的句子向量 X-n+1，平均值可以计算为：

类似地，协方差矩阵是期望:

因此它可以计算为：

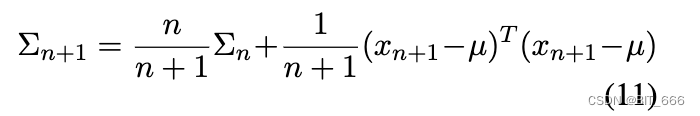
因此，我们可以得出结论，μ 和 Σ 的空间复杂度都是 O(1)，时间复杂度为 O(N)，这表明我们的算法的有效性在理论上已经达到最优。可以合理地推断，第 3.2 节中的算法即使在大规模语料库中也可以获得具有有限内存存储的协方差矩阵 Σ 和 μ。

4.Experiment

[实验]

为了评估所提出方法的有效性，我们展示了我们在多种配置下与语义文本相似性 (STS) 任务相关的各种任务的实验结果。在以下部分中，我们首先介绍第 4.1 节中的基准数据集和我们在第 4.2 节中的详细实验设置。然后，我们在第 4.3 节中列出了我们的实验结果和深入分析。此外，我们在第 4.4 节中评估了不同维度 k 设置降维的效果。

4.1 Datasets

[数据集]

我们将模型性能与 STS 任务的基线进行比较，而无需任何特定的训练数据，如 (Reimers and Gurevych, 2019) 所做的那样。7 个数据集，包括 STS 2012-2016 任务 (Agirre et al., 2012, 2013, 2014, 2015, 2016)、STS 基准 (Cer et al., 2017) 和 SICK-Relatedness 数据集 (Marelli et al., 2014) 被用作我们评估的基准。对于每个句子对，这些数据集提供从 0 到 5 的标准语义相似度测量。我们采用句子嵌入的余弦相似度与黄金标签之间的 Spearman 等级相关性，因为 (Reimers and Gurevych, 2019) 建议它是 STS 中最合理的指标任务。评估过程与 (Li et al., 2020) 相同，我们首先将每个原始句子文本编码为句子嵌入，然后计算输入句子嵌入对之间的余弦相似度作为我们的预测相似度分数。

4.2 Experimental Settings and Baselines

[实验设置与基线]

- Baselines

我们将性能与以下基线进行比较。在无监督 STS 中，Avg.GloVe 嵌入表示我们采用 GloVe (Pennington et al., 2014) 作为句子嵌入。同样，Avg.BERT 嵌入和 BERT CLS-vector 表示我们使用原始 BERT (Devlin et al., 2019)，有和没有使用 CLS-token 输出。在 surperved STS 中，USE 表示通用句子编码器 (Cer et al., 2018)，它将 LSTM 替换为 Transformer。虽然 SBERT-NLI 和 SRoBERTa-NLI 对应于在组合 NLI 数据集（原位 SNLI (Bowman et al., 2015) 和 MNLI (Williams et al., 2018)）上训练的 BERT 和 RoBERTa (Liu et al., 2019) 模型与 Sentence-BERT 训练方法（Reimers 和 Gurevych，2019）。

- Expiremental details

由于 BERTflow (NLI/target) 是我们比较的主要基线，我们基本上与他们的实验设置和符号对齐。具体来说，我们在实验中也使用了 BERT base 和 BERT large。我们选择 first-last-avg 作为我们的默认配置，因为与仅对最后一层进行平均相比，BERT 的第一层和最后一层可以稳定地获得更好的性能。与 (Li et al., 2020) 类似，我们利用完整的目标数据集（包括训练集、开发集和测试集中的所有句子，以及排除所有标签）通过第 3.2 节中描述的无监督方法计算白化参数 W 和 μ。这些模型被符号化为 whitening(target)。此外，whitening(NLI) 表示在 NLI 语料库上获得白化参数。-whitening-256 (target/NLI) 和 whitening-384 (target/NLI) 表明，通过我们的白化方法，输出嵌入大小分别减少到 256 和 384。

4.3 Results

[结果]

- Without supervision of NLI

如表 1 所示，原始 BERT 和 GloVe 句子嵌入惊奇地在这些数据集上获得了最差的性能。在 BERT-base 设置下，我们的方法始终优于 BERT-flow，并分别在 STS-B、STS12、STS-13、STS-14、STS-15 数据集上以 256 个句子嵌入维度实现了最先进的结果。当我们切换到 BERT-large 时，如果句子嵌入的维度设置为 384，则取得更好的结果。与 BERT-flow 相比，我们的方法在大多数数据集上仍然获得了具有竞争力的结果，并在 STS-B、STS-13、STS-14 数据集上实现了最先进的结果大约 1 分。

- With supervision of NLI

在表 2 中，SBERT-base 和 SBERT-large 通过 (Reimers and Gurevych, 2019) 中的方法在具有监督标签的 NLI 数据集上进行训练。可以看出，我们的 SBERT base-whitening 在STS13、STS-14、STS-15、STS-16 任务上的表现优于 BERT base-flow，SBERT large-whitening 在 STS-B、STS-14、STS-15、STS-16 任务上获得了更好的结果 BERT large-flow。这些实验结果表明，我们的白化方法可以进一步提高 SBERT 的性能，即使它是在 NLI 数据集的监督下训练的。

4.4 Effect of Dimensionality k

[维度k的影响]

降维是一个关键特征，因为减小向量大小会带来更小的内存占用和更快的下游向量搜索引擎检索。维度 k 是句子嵌入保留维度的超参数，可以在很大程度上影响模型性能。因此，我们进行了实验来测试模型的 Spearman 相关系数随维度 k 的变化的变化。图 1 显示了 BERT-base 和 BERT-large 嵌入下模型性能的变化曲线。对于大多数任务，将句子向量的维度减少到三分之一是一个相对最优解，其性能处于增加点的边缘。

上图展示了不同维度 k 与 BERT 白化对上述所有任务的影响。x 轴是句子嵌入的保留维度，y 轴是 Spearman 的相关系数。每个子图上的标记点是最优结果的位置，可以维度减少到 1/3 对向量后续检索相关的性能影响相对较小，但可以带来存储的减少和计算效率的大大提升。

在表 1 中的 SICK-R 结果中，虽然我们的 BERT base-whitening-256 (NLI) 不如 BERT base-flow (NLI) 有效:

但我们的模型具有竞争优势，即较小的嵌入大小 (256 vs. 768)。此外，如图1(a) 所示，当嵌入大小设置为 109 时，我们的 BERT base-whitening (NLI) 的相关分数上升到 66.52，比 BERT base-flow (NLI) 高 1.08 分。此外，其他任务也可以通过仔细选择 k 来实现更好的性能。

5.Conclusion

[总结]

在这项工作中，我们探索了一种缓解句子嵌入各向异性问题的替代方法。我们的方法基于机器学习中的白化操作，实验结果表明我们的方法在 7 个语义相似性基准数据集上简单有效。此外，我们还发现引入降维操作可以进一步提高模型的性能，并自然地优化内存存储并加快检索速度。

6.Personal thoughts

[个人想法]

本文提出了一种特征白化的思路，特征白化这里如果转化到数学语言中就是主成分分析，通过获取其主要方向的向量来表征自己，用更低的维度、更快的检索速度来弥补丢失的很小一部分的精度，本质上还是一个取舍和相对最优的方法。这种调和、折中的思路在机器学习中比比皆是，例如 Attention 计算里的加权平均，博主之前在 LLaMA-2 获取文本向量计算相似度一文中做了基础的实现，大家可以参考，也可以参考论文中给出的源代码: https://github.com/bojone/BERT-whitening: