复杂度（时间和空间）

一、时间复杂度

1.概念

是一个函数。算法中基本操作的执行次数。

我们来简单看几个例子。

它的算法函数式是这个：

我们再来两个：

那这几个算法谁跑的最快，谁跑的最慢啊？

大家发现其实不那么好比较，因为有好几项。但其实没那么难比较。

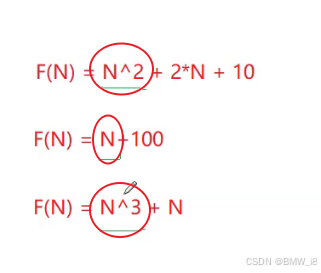
因为影响最大的项是不是这几项？后面的项影响都不大。那你可以把这三个看成这样

那这里面谁跑的最快呢？

这个跑的最快

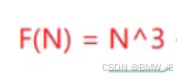
它跑的最慢

那凭什么说这个项对这个结果影响就是最大的呢？我们用另外一个理论来看一看

刚才的函数式写出来确实是我们刚才的这一个样子，我们套一些具体的值进去看一下：

那如果我们只看这一项呢？

如果这样对比就会发现：随着N越大，它后两项对这个结果影响越小。所以，时间复杂度在这个地方进行计算的时候，对这个表达式会进行一定的简化。怎么简化呢？你是一个数学的函数式，那我能不能简化一下，我去看一个大概估算呢？谁对这个表达式影响最大啊？所以它这儿会用一个大O的渐进表示法，去取它影响最大的那个项，然后进行尽可能的简化。我们刚才这个函数式简化出来以后是O(N^2)。为什么只取这一项呢？因为这一项对结果起了决定性的作用。所以我们在这个地方取的是影响最大的那个项。

再回过头来看上面的算法，如果我们把N以无限大的角度去看，你的算法算出来是它，那它的大O渐进表示法取的是

所以大家看到，取成大O的渐进表示法之后，我们在比较的时候也非常好比较。当你N取无限大的时候，其他的项是不是就没有影响了。那有人可能会说，当我N取1的时候，后面的项可是有举足轻重的影响啊。但是，我想告诉大家的是，当N取的很小时（N=1，N=10），这三个算法算法的性能是一样的，没有差异。为什么？因为N很小的时候没有比较的意义，CPU跑的非常的快。CPU有一个叫主频的概念。这个东西大概指的就是，在一个周期内它大概能执行多少指令。所以在一般的架构下面，你的主频越高，CPU处理速度越快。你的CPU再差，它每秒的运行次数也有上亿次。

我们可以写一个程序来试一下：

大家可以试一下，瞬间就运行出来了。所以N很小的时候没有区别，都是一下就运行出来了。所以我们只谈论N很大的时候。我们只进行大概的估算，估算的是算法属于那个量级。

现在来看几个常见的样例：

那它的时间复杂度是多少呢？为什么他的时间复杂度是N而不是2N呢？

其次，这个表达式里面，要把这个系数给去掉。为什么要去掉？当N无限大的时候，这个2重要吗？不重要。举个例子

你认为它们之间有差异吗？虽然它们之间有2倍的差异，但是20000亿富豪能买的东西，10000亿也能买。所以系数对这个结果影响不大的。

• 如果M远大于N，O(M)

• 如果N远大于M，O(M)

所以，一个时间复杂度的表达式上面也不一定只有一个未知数。

O(1)不是代表1次，而是代表常数次。

它的底层逻辑是这样的：

如果时间复杂度有最好，最坏和平均时，我们看最坏情况。

这里讲一件比较重要的事情：算时间复杂度不敢去看代码的循环，数循环有可能数不出来。

举个例子：

这是O(N)。

那这个呢？是log₂N次。

归纳为时间复杂度为O(logN)。为什么不写底数呢？因为对数写的时候需要支持专业公式，否则不好写底数。所以时间复杂度当中，为了方便，log₂N可以省略底数，直接写成logN。这里注意：其他底数不能省略（其他底数也很少出现）。也有人这么写log₂N------lgN，你看到能理解他什么意思就行，但这么写太不专业了。

所以，时间复杂度是logN。

讲个题外话，二分查找是个很牛的东西，我们拿暴力查找来对比一下：

显而易见吧？

它的缺点是：外墙中干，纸老虎，实际中不太实用。那它真正的问题在哪儿呢？排序不是主要的问题，因为它只要排一次之后就可以一直查找了，而排序之后获得的收益是很大的。它真正的问题在于结构，数组结构（不方便插入删除）。比如我插入一个数据，我是不是还得保持它有序啊，那我是不是得把后面的数据挪走，我才能把这个数据插进来。我要删除一个数据，我是不是得把前面的数据往前挪？所以，它的缺点也伴随的是顺序表的缺点，那有人就说了，还得上链表。链表也不行，为什么链表也不行？链表，你能说算出开始的位置，算出最后的位置。比如说，这是10万个值，你能算出第5万个，直接一把访问第5万个位置吗？链表能用二分查找吗？不能，所以，二分查找其实用的不多，简单提一下，以后我们会有一棵树叫做二叉查找（搜索）树。进化---->红黑树 、 AVL树，B树系列。

时间复杂度是O（N）。

我们在这个基础上改造一下：

这样时间复杂度是多少？O(N^2)

O(2^N)

递归时间复杂度：所有递归调用次数累加。

大O渐进法的总结

• 大O符号（Big O notation）：是用于描述函数渐进行为的数学符号

  • 推导大O阶方法：

    • 1、用常数1取代运行时间中的所有加法常数。

    • 2、在修改后的运行次数函数中，只保留最高阶项。

    • 3、如果最高阶项存在且不是1，则去除与这个项目相乘的常数。得到的结果就是大O阶。

• 本质

  • 计算算法时间复杂度（次数）属于哪个量级（level）

• O的意思就是表达我是一个估算你的量级的一个简化过的

  • 那常见的量级有那些呢？

2.常见的量级

主要就是这些：

二、空间复杂度

空间复杂度算的不是空间，因为单个对象通常的大小差异也不会说很大。那有人说，你是1字节，我是100字节那差异还不大吗？不大，这就和之前说CPU跑的很快，它不在乎几次零零碎碎的那些一样。1M我都感觉不大，所以你想单个变量的字节差异对我影响大不大？自然不大。

• 算的是变量个数

• 也使用大O渐进表示法进行简化

那我们来尝试算一下

他用了多少个变量呢？3个。

3个就是常数个。那就是O(1)，这里的数组它不算空间，为什么不算呢？记住：空间复杂度计算的是解决这个问题时，算法中额外开辟的空间。

O(N)

常见的空间复杂度：

• O(1)

• O(N)

• O(N^2)

  • 什么情况下是这个呢？

    • 二维数组

• 也会存在O(logN)的状况