贪心算法

“ 所谓贪心算法，就是不断地选取当前最优策略的方法设计算法。在问题求解时，总是做出现在看起来是最好的选择。”

​

关于贪心算法，没什么好说的，因为它没有固定的算法框架，本文通过几个问题的解决来介绍下贪心算法以及该算法的应用。

 

︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿

 

 

田忌赛马

 

田忌赛马的故事大家都听过。讲的是孙膑为田忌调整了作战策略，使得整体实力较弱的田忌的马战胜了实力较强的齐威王的马。策略也很简单，总共就分上中下三等马，用下等马对战齐王的上等马，上等马对战齐王的中等马，中等马对战齐王的下等马，这样明明整体实力较弱，但也能通过总比分2:1赢得比赛。

齐王比赛输了之后，很不服气，他认为区区三匹马的比较胜负只是运气罢了。于是，它便拿出了整个马场的马要再和田忌比一次，并告诉田忌赢一局赢200金，输一局输200金，平局就不用出钱，并且给了田忌三天时间考虑。田忌有了上次孙膑的策略之后，决定自己设计策略。

假设田忌知道自己和齐王的所有的马的跑的快慢的等级，该如何设计策略，使得田忌尽量多赢钱或者尽量少输钱。

我们结合贪心算法这个名称和这个比赛来分析一下问题。所谓贪心算法的宗旨就是一个字-----贪。放到上面例子中，就是尽可能赢多的钱。而当我们拿到一匹马，怎么才能让这匹马为我们尽可能多的赢'钱'，或者说创造尽可能多的价值呢。就算不能创造己方的直接价值，也要让对方消耗最多的价值。回到题目就是，如果这匹马有能赢过的对手马，就选择能赢过的马当中最高等级的一匹。如果这匹马遇上谁都是输，那就选择对手马中最强的一匹，死也要拉个垫背的。我们要做的是贪，榨干每匹马的价值，这就是贪心的本质。

 

为了复杂度，我们可以对双方的马先进行一个排序，然后按顺序比较过去，talk is cheap， 我们来看看伪代码。

​int main(){    1.输入你和齐王所有的马匹(共n匹)速度等级，你的存放在数组vl1,    齐王的存放在vl2中,累计的钱存放在sum中    2.将vl1,vl2降序排序    3.遍历你的马匹，逐一与齐王的作比较    for (i = 0; i < n; i++)    {        /* 标识是否有能战胜的马 */        int flag = 0;        for (j = 0; j < n; j++)        {            /* 若齐王的这匹马比过，跳过 */            if (vl2[j] == -1)  continue;            /* 若比齐王的快，标记flag */            if (vl1[i] > vl2[j])            {                flag = 1;                // 因为顺序排列过，所以最先能赢的就是能赢的                // 当中最强的，比较后将速度置为-1，认为这两匹                // 是比过的，后面不再使用。                vl1[i] = -1; vl2[j] = -1;                break;            }        }        if (flag == 1)           sum += 200；        /* 此时说明你剩余最快的马已经不比齐王最慢的马快了,           也就是你之后所有的马要么打平要么输了。 */        else        {            /* 若最快的马已经比齐王最慢的还慢了，直接扣钱，            否则标记马匹，就当无事发生 */            if (vl1[i] < vl2[n-1-i])            {                sum -= 200;            }            vl1[i] = -1; vl2[n-1-i] = -1;        }    }    4. 输出结果sum​    return 0;}

大致的程序就如上所示，事实上上述代码效率还是很低下的，时间复杂度为O(n^2)，可以通过每次修改比较的位置使复杂度达到O(n)。不过这边主要介绍贪心的思想，所以不拓展讲其他解法和优化写法了。

 

 

︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿

 

均分纸牌

 

这也是一道贪心的经典例题，虽然它贪心的不那么明显。

描述：

    

有n堆纸牌，编号分别为 1，2，…, n。每堆上有若干张，但纸牌总数必为n的倍数。可以在任一堆上取若干张纸牌，然后移动。移牌规则为：在编号为1的堆上取的纸牌，只能移到编号为 2 的堆上；在编号为 n 的堆上取的纸牌，只能移到编号为n-1的堆上；其他堆上取的纸牌，可以移到相邻左边或右边的堆上。现在要求找出一种移动方法，用最少的移动次数使每堆上纸牌数都一样多。

例如 n=4，4堆纸牌数分别为： 

①　9　②　8　③　17　④　6

移动3次可达到目的：

从 ③ 取4张牌放到④（9 8 13 10）->

从③取3张牌放到 ②（9 11 10 10）->

从②取1张牌放到①（10 10 10 10）。

思路：

1、题目中说了纸牌总数是n的倍数，那么平均值必为整数。

2、因为只能从相邻的牌堆拿牌，而且要求最少次数。所以得一次移动到位，不能来回匀。按照贪心思想（移动尽可能少的次数的情况），就是让当前牌堆一次移动就达到目标牌堆数（即平均数），缺多少就一次直接从边上拿多少。所以一开始，就把目标数定为最终需要达到的平均数就是本题的贪心思想。

3、我们逻辑上从左往右遍历，如果当前牌堆数量就是平均值，继续下一堆。如果不是平均值，我们逻辑上一定是从右边拿牌，拿的牌数为(平均值 - a[i])，即使拿的牌数是负的也没关系，因为正负仅仅表示拿进或者拿出。这样就不用考虑再从左边匀的情况，因为左边的已经之前给了你，你只需要一路往前就行了。

代码如下：

int main(){   int n, i, sum, average;   /* 输入牌堆数和每堆牌的牌数 */   scanf("%d", &n);   for (i = 0; i < n; i++)   {       scanf("%d", &a[i]);       sum += a[i];   }   /* 求得牌的平均值 */   average = sum / n;   int step = 0;      /* 遍历牌堆 */   for (i = 0; i < n; i++)   {       if (a[i] == average)           continue;       /* 只能从相邻牌堆取，所以将需要的牌数传给下一堆 */       a[i + 1] -= average - a[i];       step ++;   }      printf("%d\n", step);   return 0;}

 

 

︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿︿

 

区间调度

 

有n项工作，每项工作分别在si时间开始，在ti时间结束。对于每项工作，你都可以选择参与与否。如果选择了参与，那么自始至终都必须全程参与。此外，参与工作的时间段不能重叠（即使是开始的瞬间和结束的瞬间也是不允许重叠的）。你的目标是参与尽可能多的工作，那么最多能参与多少项工作呢？

例如

输入，

n = 5， s = {1, 2, 4, 6, 8}， t = {3, 5, 7, 9, 10}

 

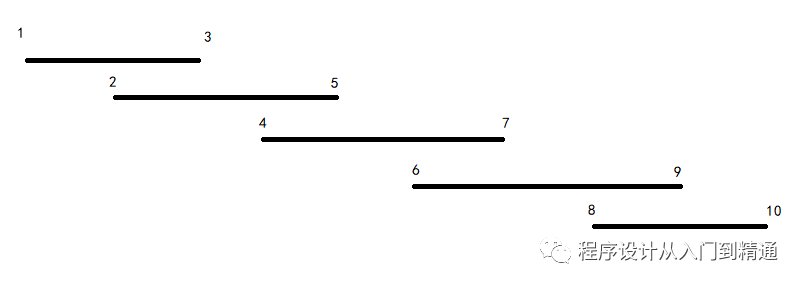
输出，

3

选取上图{1,3},{4,7},{8,10}三个工作区。

思路，

这个问题也可以通过贪心来求解，但不像前面那么简单。因为它可以贪的地方太多了。如下面几种思想，都一定程度上包含了贪心思想：

1. 在可选的工作区，每次都选取开始时间最早的工作

2. 每次都选取结束时间最早的工作

3. 每次选取用时最短的工作

4. 每次都选取与最少可选工作有重叠的工作

但是很显然，这些算法并不一定都是正确的，如果不慎重地随便选择一种思想就开始编程，就会得到错误的算法。

事实上，其中的思想2是正确的，其余的几种我们都可以找到对应的反例。或者说，在有些情况下，它们的策略并非是最优。

但是通过举反例来说明一种算法的正确与否显然不严谨。我们可以对上面思想2用以下方法证明。

1.与其他方法相比，该算法的选择方案在选取了相同数量的更早开始的工作时，其最终结束时间不会比其他方案更晚。

2.所以，不存在选取更多工作的选择方案。

使用归纳法，反证法，就可以完成严格意义上的证明（证明过程较长，再次不再赘述）

这种题通常出现在程序设计的比赛中，只要程序能够正确运行就好了，严格意义的证明并不是必须的。因此可以说，如果你有足够的自信认为算法是正确的，那就不需要证明。但是，如果不能坚信算法是正确的，并且程序不能正确输出你想要的结果时，就会搞不明白到底是算法设计有问题还是程序实现有问题。所以在实现之前，在头脑中简单地思考证明一下也是有必要的。