poj1003 -- Hangover

Hangover

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 124577		Accepted: 60791

Description

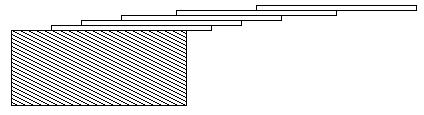
How far can you make a stack of cards overhang a table? If you have one card, you can create a maximum overhang of half a card length. (We're assuming that the cards must be perpendicular to the table.) With two cards you can make the top card overhang the bottom one by half a card length, and the bottom one overhang the table by a third of a card length, for a total maximum overhang of 1/2 + 1/3 = 5/6 card lengths. In general you can make n cards overhang by 1/2 + 1/3 + 1/4 + ... + 1/(n + 1) card lengths, where the top card overhangs the second by 1/2, the second overhangs tha third by 1/3, the third overhangs the fourth by 1/4, etc., and the bottom card overhangs the table by 1/(n + 1). This is illustrated in the figure below.

Input

The input consists of one or more test cases, followed by a line containing the number 0.00 that signals the end of the input. Each test case is a single line containing a positive floating-point number c whose value is at least 0.01 and at most 5.20; c will contain exactly three digits.

Output

For each test case, output the minimum number of cards necessary to achieve an overhang of at least c card lengths. Use the exact output format shown in the examples.

Sample Input

1.00
3.71
0.04
5.19
0.00

Sample Output

3 card(s)
61 card(s)
1 card(s)
273 card(s)

思路就是先把sum(i)=1/2+...+1/i (3<=i<=n)算出来存储在数组v（假设下标从0开始存储）里，然后根据输入的长度来遍历数组，当输入长度大于等于v[i]时，i+1即为所求。

代码如下：

#include <iostream>
#include <cstdio>
#include <vector>
using namespace std;

int main()
{
    //freopen("test.txt","r",stdin);
    double sum=0;
    vector<double> v;
    for(double i=2;i<10000;i++)  //先计算长度
    {
        sum+=1/i;
        v.push_back(sum);
    }
    double result;
    while(scanf("%lf",&result)==1&&result!=0)
    {
        for(int i=0;i<v.size();i++)
        {
            if(v[i]>=result)
            {
                printf("%d card(s)\n",i+1);
                break;
            }
        }
    }
    return 0;
}