cs229-lecture3-学习笔记

最新推荐文章于 2019-07-18 23:49:07 发布

BiggerQ

最新推荐文章于 2019-07-18 23:49:07 发布

阅读量481

点赞数

分类专栏：学习笔记文章标签： cs229

本文链接：https://blog.csdn.net/BiggerQ/article/details/38337895

版权

学习笔记专栏收录该内容

4 篇文章 0 订阅

订阅专栏

局部加权回归（locally weighted regression）

参数化算法：有固定参数来拟合数据的算法

非参数算法：参数变化的算法，例如局部加权回归（LWR）

LWR：选择参数 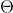$\Theta$ 使拟合最小化

$\sum_{i=1}^{m}\omega^{(i)}(y^{(i)}-\Theta^{T}x^{(i)})^{2}$ ，

其中 $\omega^{(i)}=exp(-\frac{(x^{(i)}-x)^{2}}{2\tau^{2}})$ ，

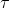即在距离目标点较近的点将获得较大的权值（ $\tau=1$ 时趋近于1），距离较远的点将获得较小的权值（ $\tau=1$ 时趋近于0），因此每次进行预测（x不同），都需要重新计算所有权值， $\tau$ 称为波长参数(bandwidth p arameter)，直观上看其控制了权值随距离增大而下降的速率，其值越小，所得的权值函数（钟型图像）越陡，反之则越平坦。

线性回归模型的概率解释

假设真实房价值与预测值之间相差一个误差项，即 $y^{(i)}=\Theta^{T}x^{(i)}+\varepsilon^{(i)}$ ，误差项 $\varepsilon^{(i)}$ 是由多个相互独立的随机变量（包括没有捕获的特征值和随机噪声等）之和，由中心极限定理，可知误差项服从均值为0的正态分布即 $\varepsilon^{(i)}\sim N(0,\sigma^{2})$ ，其概率密度函数

$P(\varepsilon^{(i)})=\frac{1}{\sqrt{2\pi}\sigma}exp(-\frac{(\varepsilon^{(i)})^{2}}{2\sigma^{2}})$

因此在给定参数的房价也是服从正态分布的，即 $(y^{(i)}|x^{(i)};\Theta)\sim N(\Theta^{T}x^{(i)},\sigma^{2})$ ，

而

$P(y^{(i)}|x^{(i)};\Theta)\\ =\frac{1}{\sqrt{2\pi}\sigma}exp(-\frac{(y^{(i)}-\Theta^{T}x^{(i)})^{2}}{2\sigma^{2}})$

令

$L(\Theta)=P(\vec{y}|X;\Theta)\\ =\prod_{i=1}^{m}P(y^{(i)}|x^{(i)};\Theta)\\ =\prod_{i=1}^{m}\frac{1}{\sqrt{2\pi}\sigma}exp(-\frac{(y^{(i)}-\Theta^{T}x^{(i)})^{2}}{2\sigma^{2}})$

所以问题变为选择参数 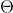$\Theta$ 使 $L(\Theta)$ 最大化，

令

$l(\Theta)=log(L(\Theta))=log(P(\vec{y}|X;\Theta))\\ =log[\prod_{i=1}^{m}\frac{1}{\sqrt{2\pi}\sigma}exp(-\frac{(y^{(i)}-\Theta^{T}x^{(i)})^{2}}{2\sigma^{2}})]\\ =\sum_{i=1}^{m}log(\frac{1}{\sqrt{2\pi}\sigma}exp(-\frac{(y^{(i)}-\Theta^{T}x^{(i)})^{2}}{2\sigma^{2}}))\\ =m\cdot log(\frac{1}{\sqrt{2\pi}\sigma})+\sum_{i=1}^{m}(-\frac{(y^{(i)}-\Theta^{T}x^{(i)})^{2}}{2\sigma^{2}})$

所以问题等同与选择参数 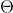$\Theta$ 使

$\sum_{i=1}^{m}(\frac{(y^{(i)}-\Theta^{T}x^{(i)})^{2}}{2})=J(\Theta)$ 最小化(注意 $\sigma$ 是正数)，

这就是线性模型中选择代价函数 $J(\Theta)$ 的原因。

logistics 回归（logistics regression）

logistics 回归算法是一种二元分类算法（输出值是个离散的，如只能取两个值0/1），

假设 $y\in\left\{ 0,1\right\},h_{\theta}(x)\in\left\{ 0,1\right\}$ ，

其假设函数为

$h_{\theta}(x)=g(\theta^{T}x)$ ，

其中 $g(z)=\frac{1}{1+e^{-z}}$ 一般被称为logistics 函数或sigmoid 函数，

图像特点：当z小于零趋向于负半轴则g(z)趋向于0，当z大于零趋向于正半轴则g(z)趋向于1，与y轴相交于(0,0.5)

所以

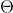$P(y=0|x;\theta)=h_{\theta}(x)\\ P(y=1|x;\theta)=1-h_{\theta}(x)$

合并得

$P(y|x;\theta)=h_{\theta}(x)^{y}(1-h_{\theta}(x))^{1-y}$

所以

$L(\Theta)=P(\vec{y}|X;\Theta)=\prod_{i=1}^{m}P(y^{(i)}|x^{(i)};\theta)\\ =\prod_{i=1}^{m}h_{\theta}(x^{(i)})^{y^{(i)}}(1-h_{\theta}(x^{(i)}))^{1-y^{(i)}}$

而