【loli的胡策】联校11.2（dp+乱搞+期望dp）

T1：

题解：

正解是个dp啦
f[i][j]表示有i个盘子，j个柱子时候的最小步数
那么f[i][j]=min{f[k][j]*2+f[i-k][j-1]}
其实还是很好理解了，整个汉诺塔的过程就是把k个盘子转移到一个塔上，把底座（i-k）转移到最后一个塔（其中，好多柱子所在的塔已被占用，就不能转移了，所以j-1），然后再把k个盘子挪到最后一个塔上
有的同学可能会说，为什么非要把k个盘子转移到一个塔上啊，两个塔不会更优吗？
其实这是一个最优化考虑，当k=1时就可以成为上面那种情况

代码：

#include <cstdio>
#include <iostream>
#define LL long long
using namespace std;
const LL INF=1e18;
LL f[70][70];int n,m,i,j,k;
int main()
{
    freopen("hanoi.in","r",stdin);
    freopen("hanoi.out","w",stdout);
    scanf("%d%d",&n,&m);
    for (i=1;i<=n;i++) f[i][3]=f[i-1][3]*2+1;
    for (i=4;i<=m;i++)
    {
        f[1][i]=1;
        for (j=2;j<=n;j++)
        {
            f[j][i]=INF;
            for (k=1;k<j;k++) 
              f[j][i]=min(f[j][i],f[k][i]*2+f[j-k][i-1]);
        }
    }
    printf("%lld",f[n][m]);
}

T2：

题解：

整体填字母的顺序是从排名为1的填到排名为n的，可以发现字典序最小并没有什么用？
考虑如果rank[i] < rank[j]，那么只要s[rank[i+1]] < s[rank[j+1]]的话两个字母就能填一样的，但是s[rank[i+1]]不能随随便便小于s[rank[j+1]]啊，小于的话等价于rank[i+1] < rank[j+1]。
如果rank[i+1]>rank[j+1]呢？那就需要填字典序下一位的字母了
如果字母用完了，-1咯！
知道了填的方法之后我们就会发现你填出来的字母相对大小不会改变！这也就是为什么字典序最小没有什么用啊

代码：

#include <cstdio>
using namespace std;
char s[200005];int n,i,rank[200005],loc[200005];
int main()
{
    freopen("rank.in","r",stdin);
    freopen("rank.out","w",stdout);
    scanf("%d",&n);
    for (i=1;i<=n;i++){scanf("%d",&rank[i]);loc[rank[i]]=i;}
    s[loc[1]]='a';int now=0;
    for (i=2;i<=n;i++)
      if (rank[loc[i-1]+1]<rank[loc[i]+1]) s[loc[i]]=s[loc[i-1]];
      else 
      {
        now++;
        s[loc[i]]=now+'a';
        if (now>=26){printf("-1");return 0;}
      }
    for (i=1;i<=n;i++) printf("%c",s[i]);
}

T3：

题解：

这个题Shallwe学长在讲的时候是模型呢。。但当时讲的高斯消元？而且处理的复杂度很大，对于本题很大的Q并不能AC，前两天还在想着找找这道题做了，呵呵，考到了，而且貌似有很优秀的做法？

———思路引自其它博主

从u到v的路径，可以分成两段：u—>lca 和 lca—>v，而去往lca的路都是由直接父亲构成的，
设u—>fa[u]的期望为f[u]
fa[u]—>u的期望为g[u]
那么柿子就出来咯！

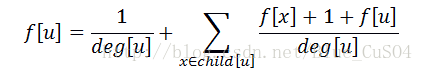
deg是每个点的出度
1/deg[u]实际上是：1*（1/deg[u]）表示直接走到父亲的期望（花费*概率）
除了直接到达目标，还有一种情况是先到u的儿子，之后从u的儿子返回u再到达fa[u]
每一个儿子的花费都是1+f[x]+f[u]，概率是1/deg[u]

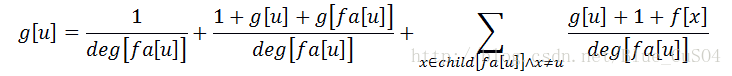
从父亲转移来也是一样的
第一种情况是直接到达u：1/deg[fa[u]]
第二种情况是先到达fa[u]的父节点，之后从fa[u]再一路回到u：花费是1+g[u]+g[fa[u]]，概率是1/deg[u]
第三种情况是先到达从fa[u]到达一个不是u的儿子——x，之后再回到fa[u]到达u：花费是1+g[u]+f[x]，概率是1/deg[u]

那我们画个柿子咯！

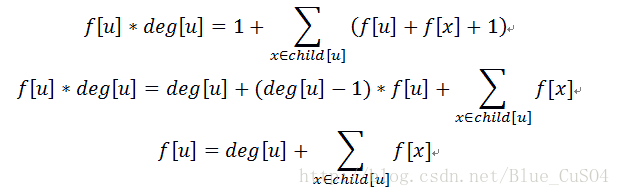
哇真是优美
那另一个柿子也是可以用这种方法画
直接出结果咯

f的求解我们从下往上，g的求解我们从上往下

这样我们就能通过两遍dfs求出f和g数组了
求出前缀和，这样就可以在处理询问时候用logn的时间求出lca之后O(1)出解

注意：f[1]=0，g[1]=0，因为1节点没有父亲！

代码：

#include <cstdio>
#include <cstring>
#include <iostream>
#define LL long long
#define N 100005
#define sz 19
using namespace std;
const int mod=1e9+7;
int tot,nxt[N*2],point[N],v[N*2];
int f[N][sz],mi[sz],du[N],father[N],ff[N],gg[N],h[N];
void addline(int x,int y)
{
    ++tot; nxt[tot]=point[x]; point[x]=tot; v[tot]=y;
    ++tot; nxt[tot]=point[y]; point[y]=tot; v[tot]=x;
}
void dfs(int x,int fa)
{
    h[x]=h[fa]+1;
    father[x]=fa;
    for (int i=1;i<sz;i++)
      if (h[x]<mi[i]) break;
      else f[x][i]=f[f[x][i-1]][i-1];
    for (int i=point[x];i;i=nxt[i])
      if (v[i]!=fa)
      {
        f[v[i]][0]=x;
        dfs(v[i],x);
      }
}
int lca(int x,int y)
{
    if (h[x]<h[y]) swap(x,y);
    int k=h[x]-h[y];
    for (int i=0;i<sz;i++)
      if ((k>>i)&1) x=f[x][i];
    if (x==y) return x;
    for (int i=sz-1;i>=0;i--)
      if (f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i];
    return f[x][0];
}
void dfsf(int x,int fa)
{
    for (int i=point[x];i;i=nxt[i])
      if (v[i]!=fa)
      {
        dfsf(v[i],x);
        ff[x]=(ff[x]+ff[v[i]])%mod;
      }
    ff[x]=(ff[x]+du[x])%mod;
}
void dfsg(int x,int fa)
{
    LL sum=0;
    for (int i=point[x];i;i=nxt[i])
      if (v[i]!=fa) sum=(sum+ff[v[i]])%mod;
      else sum=(sum+gg[x])%mod; 
    for (int i=point[x];i;i=nxt[i])
      if (v[i]!=fa)
      {
        gg[v[i]]=(du[x]+sum-ff[v[i]])%mod;
        dfsg(v[i],x);
      }
}
void qzh(int x,int fa)
{
    ff[x]=(ff[x]+ff[fa])%mod;
    gg[x]=(gg[x]+gg[fa])%mod;
    for (int i=point[x];i;i=nxt[i])
      if (v[i]!=fa) qzh(v[i],x);
}
int main()
{
    freopen("tree.in","r",stdin);
    freopen("tree.out","w",stdout);
    int i,n,q;
    mi[0]=1;
    for (i=1;i<sz;i++) mi[i]=mi[i-1]*2;
    scanf("%d%d",&n,&q);
    for (i=1;i<n;i++)
    {
        int x,y;
        scanf("%d%d",&x,&y);
        addline(x,y); du[x]++; du[y]++;
    }
    dfsf(1,0);
    ff[1]=0;//根节点没有父亲，到父亲的期望为0 
    dfsg(1,0);
    gg[1]=0;
    qzh(1,0);
    dfs(1,0);
    while (q--)
    {
        int x,y;
        scanf("%d%d",&x,&y);
        int fa=lca(x,y);
        LL ans=(ff[x]-ff[fa]+gg[y]-gg[fa]+mod)%mod;
        printf("%lld\n",ans);
    }
}

总结：

今天算是很失败的了，T1以为是找规律然后找不到什么科学的规律就GG了，完全没去想什么dp啊
T2看到后缀数组就懵逼了，在加上字符串很辣鸡，打暴力滚粗；
T3是当时Shallwe学长讲期望的时候的模型题目，他当时说要高斯消元？！我怎么可能会这种东西，就看了一眼没有深入思考，时间分布极为不均。。
然而T1T2都是比较简单的题目。。。。。看来还是要多思考啊