后缀自动机学习笔记

最新推荐文章于 2020-05-16 15:34:19 发布

wwyx2001

最新推荐文章于 2020-05-16 15:34:19 发布

阅读量451

点赞数 2

分类专栏：学习笔记后缀自动机文章标签：学习笔记后缀自动机

本文链接：https://blog.csdn.net/Blue_CuSO4/article/details/79343982

版权

学习笔记同时被 2 个专栏收录

25 篇文章 0 订阅

订阅专栏

后缀自动机

13 篇文章 0 订阅

订阅专栏

因为喵喵喵实在是太zz了发现BJ初三的dalao就会SAM，赶快跑回来自己学习。好麻烦啊翻了一堆讲义总算弄明白一些了，写个学习笔记加深印象吧。

什么是后缀自动机？

后缀自动机顾名思义就是一棵包含了原串s所有后缀的字母树。如果直接像构建trie树的方式构建节点数应该是|S|^2，这个空间显然承受不住。

一坨定义

ch[x][s]表示的是节点x（也可以说是状态）字符s的节点编号。返回该结点对应的子串加上某个字符后生成的合法子串在后缀自动机中所对应的位置(其实就和字母树一样),如果该指针不存在,就说明这样的子串是不存在的(即不是s的子串)

fa[x]其实就是parent指针，但是注意这里的fa[x]表示的并不是他的父亲是谁，因为上面也说过了一个节点因为代表了多个含义所以他也有多个父亲。parent指针指向的位置表示的是上一个可接受态

right(s)表示的子串s在原串中所有出现位置的右端点的集合。
举个例子来说，在串S=“aabbcaaa”中，“aa”这个子串出现的位置有[1,2]，[5,6]，[6,7]这三个，那么如果在S的后缀自动机上跑“aa”这个子串到达节点s，那么节点s所代表的集合就是{2,6,7}，也就是它所有出现位置的右端点集合，这就是所谓的Right集合。
对于right满足right(s)是right(fa(s))的子集。right的求法，按照parent树中深度从大到小，依次将每个状态的right集合并入他fa状态的right集合。

step[x]表示的是从根节点到该节点的最大距离，对于一个状态s,他代表的串的长度区间就是(len[fa],len[x]]，这同时也是这个状态代表的字符串个数

后缀自动机的构造

这里写图片描述
以经典的aabbabd为例：

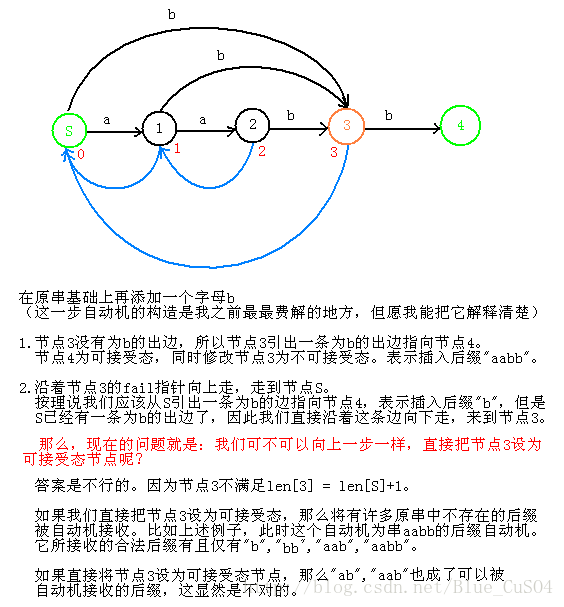
以上引自这位up

构造模板

#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
char st[100000];int ch[100000][30],tot=1,last=1,np,p,q,nq,fa[100000],step[100000];
void insert(int c)
{
    p=last; np=last=++tot;
    step[np]=step[p]+1;
    while (ch[p][c]==0 && p!=0) ch[p][c]=np,p=fa[p];
    if (p==0){fa[np]=1;return;}
    q=ch[p][c];
    if (step[q]==step[p]+1) {fa[np]=q;return;}
    nq=++tot; step[nq]=step[p]+1;
    memcpy(ch[nq],ch[q],sizeof(ch[q]));
    fa[nq]=fa[q]; fa[q]=fa[np]=nq;
    while (ch[p][c]==q) ch[p][c]=nq,p=fa[p]; 
}
int main()
{
    scanf("%s",st);
    int len=strlen(st);
    for (int i=0;i<len;i++) 
      insert(st[i]-'a');
}

后缀自动机的应用

公共子串问题

诶两个串的我会，后缀数组？把两个串连在一起然后看sa分别在两个串里的最大height值

其实用后缀自动机也是ok的，我们将A串建立后缀自动机，然后B串进行匹配，因为后缀自动机中包含A串的所有子串，并且root到后缀自动机中的任意节点形成的路径都是A的合法子串，所以B能匹配到的根到点的最长路径就是AB的最长公共子串。如果匹配到一个点之后匹配不上怎么办啊？这里后缀自动机的parent指针和AC自动机里的fail指针差不多，每个点的parent指针指向的是上一个可以接受后缀的节点，那么如果当前节点可以接某个后缀那个parent指针指向的也可以接咯，那么匹配不上我们就跳parent，直到匹配上或者到根节点为止，跳到一个节点后当前匹配的长度就变成step[i]了

要是一堆串呢？对第一个串建立后缀自动机，不过这次匹配的时候是多个串进行匹配。每次匹配的时候对于后缀自动机中的每个节点维护一个值h，表示的是到达该节点所能匹配上的最大长度。光匹配还不够，我们需要按照拓扑序倒序，用每个节点取更新他的parent节点，因为如果匹配到一个状态，那么实际上他parent链上的所有状态都匹配上了。然后对于每个串匹配后得到的每个位置的h数组取min得到数组g（这是对于所有串每个位置的横向比较，长的字符串可以将就短的，但是短的不能将就长的啊），g数组再取最大值就是一个纵向比较，这样一横一纵，对于所有位置的所有字符串就可以得到比较了。
PS：所谓的拓扑倒序就是按照step从大到小。

BZOJ2946 & SPOJ1812 LCS2

第K小子串问题

因为后缀自动机可以识别串S的所有子串，所以它是解决这类问题十分方便的一个方法。我们可以顺着自动机这个有向无环图来DFS，对于每个节点预处理它往后还能经过多少不同的子串，再决定走哪条路就可以了：如果他的儿子的size>=k就说明第k小的子串的结尾在该子树中，否则k-size，然后从下个继续。有点主席树查询区间k大的意思。

这个预处理就相当于求DAG中一个节点往后还有多少不同的路径，是一个简单的DP，每次枚举当前节点的所有儿子它们累加过来就可以了。如果是相同子串不重复计算，每个点的初始权值就是1；否则每个点的初始权值就是它Right集合的大小。这种时候要特别注意输出的时候减去的也是Right集合的大小而不是1

BZOJ3998 弦论

重复出现的子串问题

这类问题大多数是利用Right集合的性质，因为一个节点代表的字符串一定在Right集合包含的所有位置上重复出现。我们没有必要为每个节点保存它的Right集合，因为它的Right集合一定是所有fa指针指到它的节点的Right集合的并集，而这些节点的Right集合又是互不相交的，所以想要得到关于每个节点Right集合的信息，只需要在建立自动机以后按照拓扑序从后往前，用每个节点来更新它的fa节点就可以了。

以SPOJ8222为例，它要求每种长度的串出现次数的最大值，那么只需要对于每个节点递推出它的Right集合大小，然后映射到长度上面去就可以了。需要注意的一个问题就是如果长度为i的串出现了k次，那么长度为i-1的串一定至少出现了k次，因为可以取那些串的后缀。所以最后还要用F(i)去更新一下F(i-1)。

SPOJ8222
CF235C