引言:
在关联分析中,频繁项集的挖掘最常用到的就是Apriori算法。Apriori算法是一种先产生候选项集再检验是否频繁的“产生-测试”的方法。这种方法有种弊端:当数据集很大的时候,需要不断扫描数据集造成运行效率很低。
而FP-Growth算法就很好地解决了这个问题。它的思路是把数据集中的事务映射到一棵FP-Tree上面,再根据这棵树找出频繁项集。FP-Tree的构建过程只需要扫描两次数据集。
更多关联分析和Apriori算法的信息请见:什么是关联分析、Apriori算法的介绍。
正言:
我们还是用购物篮的数据:
TID Items 001 Cola, Egg, Ham 002 Cola, Diaper, Beer 003 Cola, Diaper, Beer, Ham 004 Diaper, Beer TID代表交易流水号,Items代表一次交易的商品。
首先,FP-Growth算法的任务是找出数据集中的频繁项集。
然后,FP-Growth算法的步骤,大体上可以分成两步:(1)FP-Tree的构建; (2)FP-Tree上频繁项集的挖掘。
FP-Tree的构造:
- 扫描一遍数据库,找出频繁项的列表
L
,按照支持度计数递减排序。即:
L = <(Cola:3), (Diaper:3), (Beer:3), (Ham:2)> - 再次扫描数据库,由每个事务不断构建FP-Tree:
①FP-Tree的根节点为 null 。
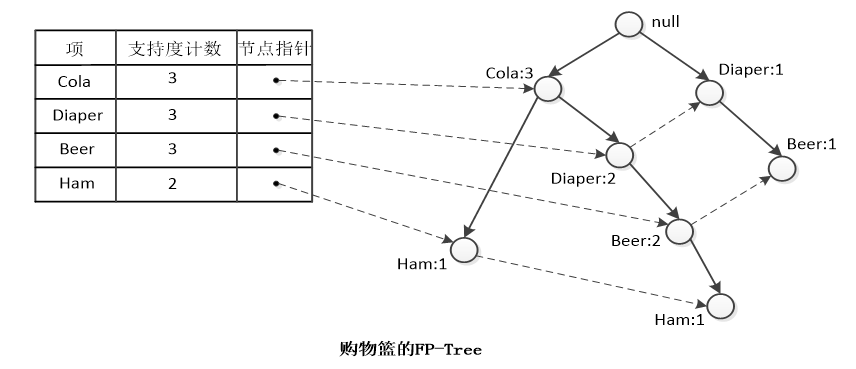
②从数据库中取出事务,按照 L 排序,然后把每个项逐个添加到FP-Tree的分枝上去。例如,事务001排序后为{Cola, Ham},在根节点上加一棵子树Cola-Ham。事务002排序后为{Cola, Diaper, Beer},因为根节点上已经有个子树节点“Cola”,所以可以共用该节点,在Cola节点上加一棵子树Diaper-Beer,同时Cola的计数加1。事务003可与树共用节点Cola-Diaper-Beer,所以只需在Beer后面加个子树节点“Ham”,同时把Cola、Diaper、Beer的计数加 1 即可。········· - FP-Tree还有一样东西:头结点表。作用是将所有相同的项链接起来,这样比较容易遍历。
最后得到的FP-Tree如下:
构造FP-Tree的伪代码如下:
算法:FP-Tree构造算法
输入:事务数据集 D,最小支持度阈值 min_sup
输出:FP-Tree
(1) 扫描事务数据集 D 一次,获得频繁项的集合 F 和其中每个频繁项的支持度。对 F 中的所有频繁项按其支持度进行降序排序,结果为频繁项表 L ;
(2) 创建一个 FP-Tree 的根节点 T,标记为“null”;
(3) for 事务数据集 D 中每个事务 Trans do
(4) 对 Trans 中的所有频繁项按照 L 中的次序排序;
(5) 对排序后的频繁项表以 [p|P] 格式表示,其中 p 是第一个元素,而 P 是频繁项表中除去 p 后剩余元素组成的项表;
(6) 调用函数 insert_tree( [p|P], T );
(7) end for
insert_tree( [p|P], root)
(1) if root 有孩子节点 N and N.item-name=p.item-name then
(2) N.count++;
(3) Else
(4) 创建新节点 N;
(5) N.item-name=p.item-name;
(6) N.count++;
(7) p.parent=root;
(8) 将 N.node-link 指向树中与它同项目名的节点;
(9) end if
(10) if P 非空 then
(11) 把 P 的第一项目赋值给 p,并把它从 P 中删除;
(12) 递归调用 insert_tree( [p|P], N);
(13) end if
从FP-Tree提取频繁项集:
相对而言,FP-Tree的构造比较简单,而从FP-Tree提取频繁项集比较难理解。其中出现了几个新名词,下面直接针对购物篮的FP-Tree进行讲解吧。
求以“Ham”为后缀的频繁项集:
- 根据头结点表找出“Ham”结尾的路径:
< Cola:3, Ham:1 > 和< Cola:3, Diaper:2, Beer:2, Ham:1 > ,代表的意义是:原数据集中(Cola, Ham)和(Cola, Diaper, Beer, Ham)各出现了一次。 - “Ham”的两个前缀路径{(Cola:1), (Cola Diaper Beer:1)}构成了“Ham”的条件模式基,注意条件模式基的计数都定义为了“Ham”的计数。
- 根据条件模式基构建“Ham”的条件FP-树:因为在Ham的条件模式基中 Diaper、Beer 只出现了一次,Coal 出现了两次,所以 Diaper、Beer 是非频繁项,不包含在Ham的条件FP-树中。
- “Ham”的条件FP-树只有一个分支
< Cola:2 > ,得到条件频繁项集 {Cola:2}。 - 条件频繁项集 {Cola:2} 和后缀模式“Ham”合并,得到频繁项集 {Cola Ham:2}。
求以“Beer”为后缀的频繁项集:
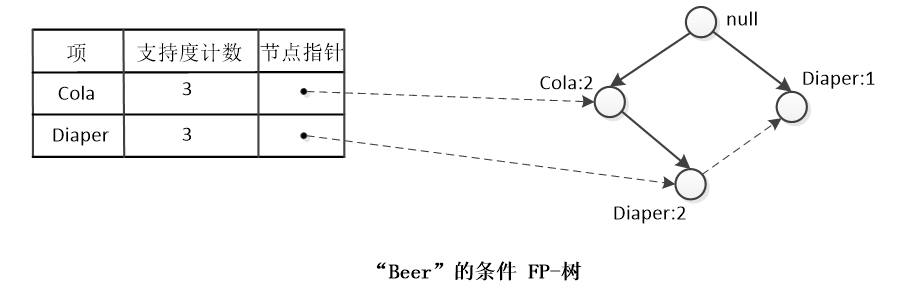
- “Beer”的条件模式基有{(Cola Diaper:2), (Diaper:1)}。
- “Beer”的条件FP-树如下。
- “Beer”为后缀的频繁项集为 {Cola Diaper Beer:2}、{Diaper Beer:2}、{Cola Beer:2}
求以“Diaper”为后缀的频繁项集:
条件模式基为{(Cola:2)},最后求得频繁项集为{Cola Diaper:2}。
综上,得到的频繁项集有:{Cola Ham:2}、{Cola Beer:2}、{Diaper Beer:3}、{Cola Diaper:2}、{Cola Diaper Beer:2}。
从FP-Tree提取频繁项集的主要步骤是:
- 对于每个频繁项,通过以下步骤求它的条件频繁项集:
- 找出它的条件模式基
- 把条件模式基当做事务集去建造一棵树,这棵树不叫FP-Tree,而叫做该频繁项的条件FP-Tree。
- 对这棵条件FP-Tree递归以上操作,即找这棵条件FP-Tree上的子条件频繁项集。
- 以上找到的都是该频繁项的条件频繁项集而已,所以每次递归都需要把条件频繁项集和该频繁项拼接起来才是我们最终要求的频繁项集
伪代码如下:
算法:FP-Growth(FP-Tree,
α );
输入:已经构造好的 FP-Tree,项集 α (初值为空),最小支持度 min_sup;
输出:事务数据集 D 中的频繁项集 L;
(1) L 初值为空
(2) if Tree 只包含单个路径 P then
(3) for 路径 P 中节点的每个组合(记为 β ) do
(4) 产生项目集 α∪β ,其支持度 support 等于 β 中节点的最小支持度数;
(5) return L = L ∪ 支持度数大于 min_sup 的项目集 β∪α
(6) else //包含多个路径
(7) for Tree 的头表中的每个频繁项 αf do
(8) 产生一个项目集 β = αf∪α ,其支持度等于 αf 的支持度;
(9) 构造 β 的条件模式基 B,并根据该条件模式基 B 构造 β 的条件 FP- 树 Treeβ ;
(10) if Treeβ≠Φ then
(11) 递归调用 FP-Growth( Treeβ , β );
(12) end if
(13) end for
(14) end if
用python语言实现 FP-Growth 的介绍请见:FP_Growth算法python实现。
转载请注明出处,谢谢!(原文链接:http://blog.csdn.net/bone_ace/article/details/46669699)











 本文详细介绍了FP-Growth算法的原理与应用,包括其如何构建FP-Tree来高效地找出数据集中的频繁项集。通过购物篮数据的实例,解释了FP-Growth算法的步骤,从FP-Tree的构建到频繁项集的提取,展示了其在关联分析领域的优势。
本文详细介绍了FP-Growth算法的原理与应用,包括其如何构建FP-Tree来高效地找出数据集中的频繁项集。通过购物篮数据的实例,解释了FP-Growth算法的步骤,从FP-Tree的构建到频繁项集的提取,展示了其在关联分析领域的优势。
















 7346
7346

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








