POJ 1328

题意：假设海岸线是一条无限延伸的直线。陆地在海岸线的一侧，而海洋在另一侧。每一个小的岛屿是海洋上的一个点。雷达坐落于海岸线上，只能覆盖d距离，所以如果小岛能够被覆盖到的话，它们之间的距离最多为d。题目要求计算出能够覆盖给出的所有岛屿的最少雷达数目。

在岛屿纵坐标小于0或者岛屿纵坐标距离海岸线大于雷达覆盖距离，或者雷达覆盖距离小于等于0，这三种情况下应该直接输出-1；

其他的情况，应该就是正常情况，进入计算最小雷达数目。

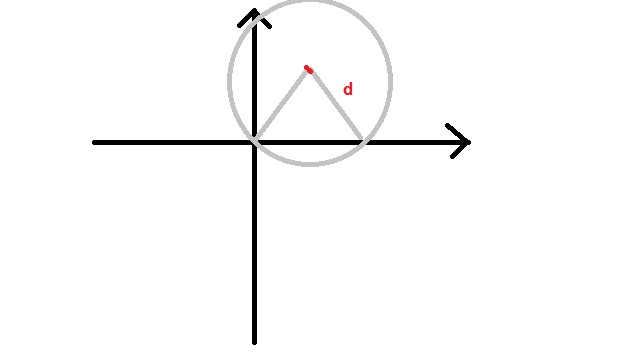
如上图，红色的点为岛屿，那么能够覆盖到此岛屿的雷达所在的区间，应该就是以该岛屿为圆心的圆与x轴交点所在的区间。

这样，我们就可以计算出所有岛屿的雷达所在的区间，得到一个区间数组。

我们将这个数组按照区间左部分进行排序，那么重叠部分就表明这些岛屿的雷达可以共用一个。从而计算出最终解。

#include<stdio.h>
#include<algorithm>
#include<math.h>

using namespace std;

struct Node
{
    double l,r;
}arr[1123];
int cmp(struct Node a,struct Node b)
{
    return a.l<b.l;
}
int main()
{
    int n,m;
    int x=1;
    while(~scanf("%d%d",&n,&m) && (m+n))
    {
        int a,b;
        int flag=0;
        for(int i=0;i<n;i++)
        {
            scanf("%d%d",&a,&b);
            arr[i].l=a-sqrt(m*m-b*b);
            arr[i].r=a+sqrt(m*m-b*b);
            if(b>m || m<=0 || b<0)
                flag=1;
        }
        if(flag)
        {
            printf("Case %d: -1\n",x++);
            continue;
        }
        sort(arr,arr+n,cmp);
        double xxx=arr[0].r;
        int count=1;
        for(int i=1;i<n;i++)
        {
            if(arr[i].l>xxx)
            {
                count++;
                xxx=arr[i].r;
            }
            else if(arr[i].r<xxx)
                xxx=arr[i].r;
        }
        printf("Case %d: %d\n",x++,count);
    }
    return 0;
}