1 复数及程序实现
来自《linux c编程一站式学习》 7.2节第1题:在本节的基础上实现一个打印复数的函数,打印的格式是 x+yi,如果实部或虚部为0则省略,例如:1.0、-2.0i、-1.0+2.0i、1.0-2.0i。最后编写一个main函数测试本节的所有代码。
-----------------------------------------------
#include <math.h>
#include <stdio.h>
struct complex_struct {
double x, y;
};
double real_part(struct complex_struct z)
{
return z.x;
}
double img_part(struct complex_struct z)
{
return z.y;
}
double magnitude(struct complex_struct z)
{
return sqrt(z.x * z.x + z.y * z.y);
}
double angle(struct complex_struct z)
{
return atan2(z.y, z.x);
}
struct complex_struct make_from_real_img(double x, double y)
{
struct complex_struct z;
z.x = x;
z.y = y;
return z;
}
struct complex_struct make_from_mag_ang(double r, double A)
{
struct complex_struct z;
z.x = r * cos(A);
z.y = r * sin(A);
return z;
}
struct complex_struct add_complex(struct complex_struct z1, struct complex_struct z2)
{
return make_from_real_img(real_part(z1) + real_part(z2), img_part(z1) + img_part(z2));
}
struct complex_struct sub_complex(struct complex_struct z1, struct complex_struct z2)
{
return make_from_real_img(real_part(z1) - real_part(z2), img_part(z1) - img_part(z2));
}
struct complex_struct mul_complex(struct complex_struct z1, struct complex_struct z2)
{
return make_from_mag_ang(magnitude(z1) * magnitude(z2), angle(z1) + angle(z2));
}
struct complex_struct div_complex(struct complex_struct z1, struct complex_struct z2)
{
return make_from_mag_ang(magnitude(z1) / magnitude(z2), angle(z1) - angle(z2));
}
void print_complex(struct complex_struct z)
{
if (z.x==0 && z.y ==0)
printf("0\n");
else if (z.x==0 && z.y!=0)
printf("%fi\n",z.y);
else if (z.x!=0 && z.y==0)
printf("%f\n",z.x);
else
printf("%f + %fi\n", z.x, z.y);
}
int main(void)
{
struct complex_struct z1 = {3.0, 4.0};
struct complex_struct z2 = {3.0, 6.0};
struct complex_struct z;
z = add_complex(z1, z2);
print_complex(z);
z = sub_complex(z2, z1);
print_complex(z);
struct complex_struct z3 = {6.0, 3.0};
z = mul_complex(z2, z3);
print_complex(z);
z = div_complex(z3, z2);
print_complex(z);
return 0;
}
程序的输出如下:
[root@redhat-beijing test]# gcc -Wall -lm complex_struct.c -o complex_struct
[root@redhat-beijing test]# ./complex_struct
6.000000 + 10.000000i
2.000000i
0.000000 + 45.000000i
0.800000 + -0.600000i
---------------改用极坐标来存储----------------
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
struct complex_struct {
double r, A;
};
double real_part(struct complex_struct z)
{
return z.r * cos(z.A);
}
double img_part(struct complex_struct z)
{
return z.r * sin(z.A);
}
double magnitude(struct complex_struct z)
{
return z.r;
}
double angle(struct complex_struct z)
{
return z.A;
}
struct complex_struct make_from_real_img(double x, double y)
{
struct complex_struct z;
z.A = atan2(y, x);
z.r = sqrt(x * x + y * y);
return z;
}
struct complex_struct make_from_mag_ang(double r, double A)
{
struct complex_struct z;
z.r = r;
z.A = A;
return z;
}
struct complex_struct add_complex(struct complex_struct z1, struct complex_struct z2)
{
return make_from_real_img(real_part(z1) + real_part(z2),
img_part(z1) + img_part(z2));
}
struct complex_struct sub_complex(struct complex_struct z1, struct complex_struct z2)
{
return make_from_real_img(real_part(z1) - real_part(z2),
img_part(z1) - img_part(z2));
}
struct complex_struct mul_complex(struct complex_struct z1, struct complex_struct z2)
{
return make_from_mag_ang(magnitude(z1) * magnitude(z2),
angle(z1) + angle(z2));
}
struct complex_struct div_complex(struct complex_struct z1, struct complex_struct z2)
{
return make_from_mag_ang(magnitude(z1) / magnitude(z2),
angle(z1) - angle(z2));
}
//打印复数 属于复数运算层,调用复数表示层
void printf_complex(struct complex_struct z)
{
if(abs(real_part(z))<0.1&&abs(img_part(z))>=0.1) //浮点型不能直接判断是否为0,这里因为输出只保留小数点后1位,所以认为小于0.1的就为0
printf("%.1fi\n",img_part(z));
else if(abs(real_part(z))>=0.1&&abs(img_part(z))<0.1)
printf("%.1f\n",real_part(z));
else if(abs(real_part(z))<0.1&&abs(img_part(z))<0.1)
printf("0\n");
else
printf("%.1f+%.1fi\n",real_part(z),img_part(z));
}
int main(void)
{
struct complex_struct z1=make_from_real_img(0,2);
struct complex_struct z2=make_from_real_img(0,1);
printf("z1+z2="); printf_complex(add_complex(z1,z2));
printf("z1-z2="); printf_complex(sub_complex(z1,z2));
printf("z1*z2="); printf_complex(mul_complex(z1,z2));
printf("z1/z2="); printf_complex(div_complex(z1,z2));
return 0;
}
程序输出:
[root@redhat-beijing test]# gcc -Wall -lm complex_struct.c -o complex_struct
[root@redhat-beijing test]# ./complex_struct
z1+z2=3.0i
z1-z2=1.0i
z1*z2=-2.0
z1/z2=2.0
[root@redhat-beijing test]#
--------------以下为复数的知识-----------------
复数,为实数的延伸,它使任一多项式方程式都有根。复数当中有个“虚数单位” ,它是
,它是 的一个平方根,即
的一个平方根,即 。任一复数都可表达为
。任一复数都可表达为 ,其中
,其中 及
及 皆为实数,分别称为复数之“实部”和“虚部”。
皆为实数,分别称为复数之“实部”和“虚部”。
欧拉公式:
-
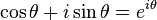 ,
,
符号表示
尽管可以使用其他表示法,复数通常写为如下形式
-
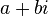 ,
,
这里的a和b是实数,而i是虚数单位,它有着性质i ² = −1。实数a叫做复数的实部,而实数b叫做复数的虚部。实数可以被认为是虚部为零的复数;就是说实数a等价于复数a+0i。实部为零且虚部不为零的复数也被称作“纯虚数”。
运算
通过形式上应用代数的结合律、交换律和分配律,再加上等式i ² = −1,定义复数的加法、减法、乘法和除法:
从极坐标形式到笛卡儿坐标形式的转换
从笛卡尔坐标形式到极坐标形式的转换
前面的公式要求非常繁杂的情况区分。但是很多编程语言提供了经常叫做atan2一个变体的反正切函数来处理这些细节。使用反余弦函数的公式要求更少的情况区分:
极坐标形式的符号
极坐标形式的符号
-
 ,
,
被叫做“三角形式”。有时使用符号cis φ简写cosφ + isinφ。 使用欧拉公式还可以写为
这叫做“指数形式”。
极坐标形式下的乘法、除法、指数和开方根
在极坐标形式下乘法、除法、指数和开方根要比笛卡尔形式下容易许多。
使用三角恒等式得到
-
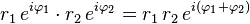 ,
,
和
-
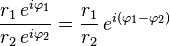 。
。
依据棣莫弗定理做整数幂的指数运算,
-
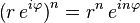 。
。
2 分数及结构体实现
实现一个用分子分母的格式来表示有理数的结构体rational以及相关的函
数,rational结构体之间可以做加减乘除运算,运算的结果仍然是rational。
测试代码如下:
int main(void)
{
struct rational a = make_rational(1, 8); /* a=1/8 */
struct rational b = make_rational(-1, 8); /* b=-1/8 */
print_rational(add_rational(a, b));
print_rational(sub_rational(a, b));
print_rational(mul_rational(a, b));
print_rational(div_rational(a, b));
return 0; }
注意要约分为最简分数,例如1/8和-1/8相减的打印结果应该是1/4而不是2/8,
可以利用第 3 节 “递归”练习题中的Euclid算法来约分。在动手编程之前先思
考一下这个问题实现了什么样的数据抽象,抽象层应该由哪些函数组成。
#include <stdio.h>
#include <stdlib.h>
struct rational {
int a,b;
};
struct rational make_rational(int a,int b)
{
struct rational z;
z.a=a;
z.b=b;
return z;
}
struct rational add_rational(struct rational a,struct rational b)
{
struct rational c;
c.a=a.a*b.b+a.b*b.a;
c.b=a.b*b.b;
return c;
}
struct rational sub_rational(struct rational a,struct rational b)
{
struct rational c;
c.a=a.a*b.b-a.b*b.a;
c.b=a.b*b.b;
return c;
}
struct rational mul_rational(struct rational a,struct rational b)
{
struct rational c;
c.a=a.a*b.a;
c.b=a.b*b.b;
return c;
}
struct rational div_rational(struct rational a,struct rational b)
{
struct rational c;
c.a=a.a*b.b;
c.b=a.b*b.a;
return c;
}
int gcd (int a,int b)
{
if(b==0)
return abs(a);
else
return gcd(b,a%b);
}
void print_rational(struct rational a)
{
int ra_gcd=gcd(a.a,a.b);
a.a=a.a/ra_gcd;
a.b=a.b/ra_gcd;
if(a.a==0)
printf("0\n");
else if(abs(a.b)==1)
printf("%d\n",a.a/a.b);
else
printf("%d/%d\n",a.a,a.b);
}
int main(int argc, char* argv[])
{
struct rational a = make_rational(1, 8); /* a=1/8 */
struct rational b = make_rational(-1, 8); /* b=-1/8 */
print_rational(add_rational(a, b));
print_rational(sub_rational(a, b));
print_rational(mul_rational(a, b));
print_rational(div_rational(a, b));
return 0;
system("pause");
}
程序的输出:
[root@redhat-beijing test]# gcc -Wall -lm rational.c -o rational
[root@redhat-beijing test]# ./rational
0
1/4
-1/64
-1
[root@redhat-beijing test]#










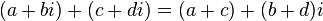
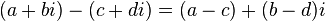


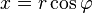
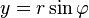
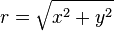

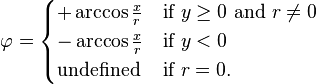















 793
793

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








