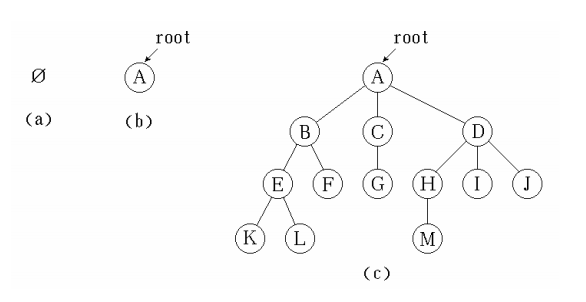
1、树的定义
2、相关概念
- 树的结点包含一个数据及若干指向子树的分支
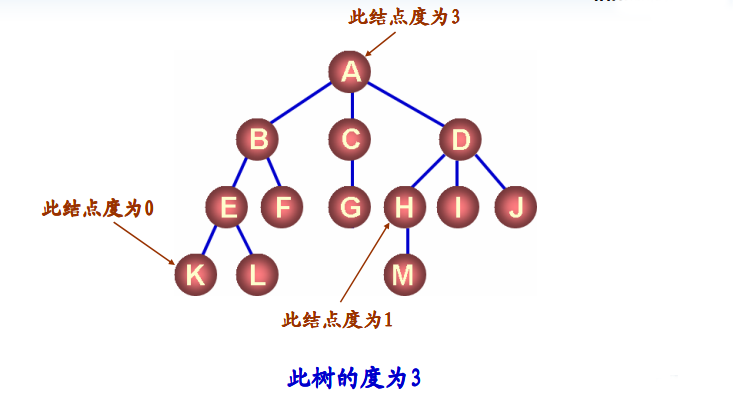
- 结点拥有的子树数称为结点的度
- 度为0的结点称为叶结点
- 度不为0的结点称为分支结点
- 树的度定义为所有结点中的度的最大值
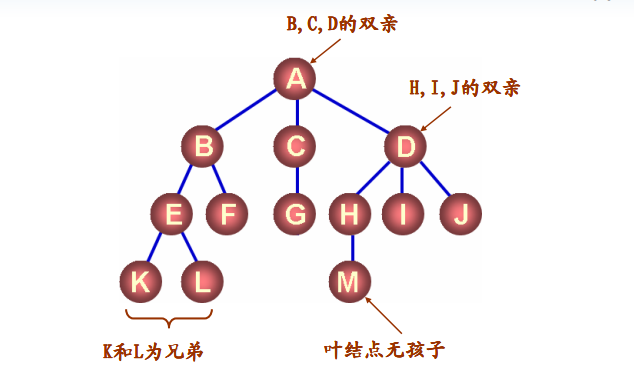
- 结点的直接后继称为该结点的孩子
- 相应的,该结点称为孩子的双亲
- 结点的孩子的孩子的……称为该结点的子孙
- 相应的,该结点称为子孙的祖先
- 同一个双亲的孩子之间互称兄弟
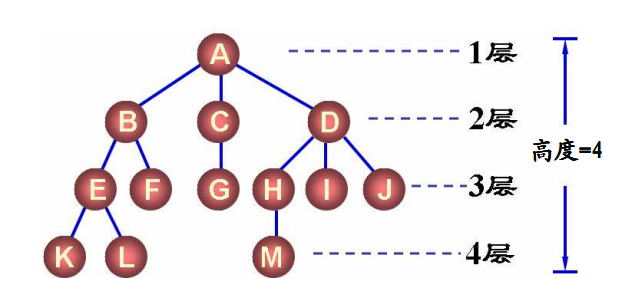
- 结点的层次
- 根为第1层
- 根的孩子为第2层
- ……
- 树中结点的最大层次称为树的深度或高度
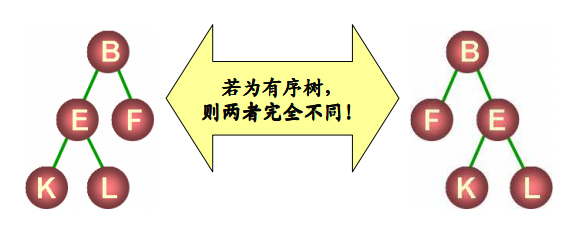
- 如果树中结点的各子树从左向右是有次序的,子树间不能互换位置,则称该树为有序树,否则为无序树。
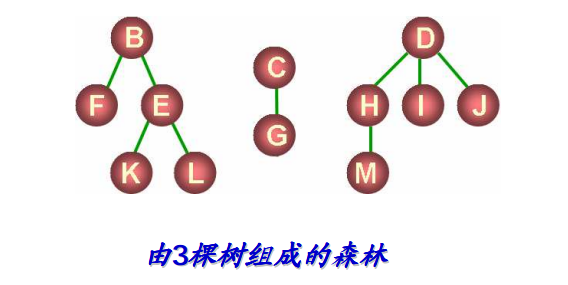
- 森林是由n (n ≥ 0 ) 棵互不相交的树组成的集合
3、小结
4、树的存储结构
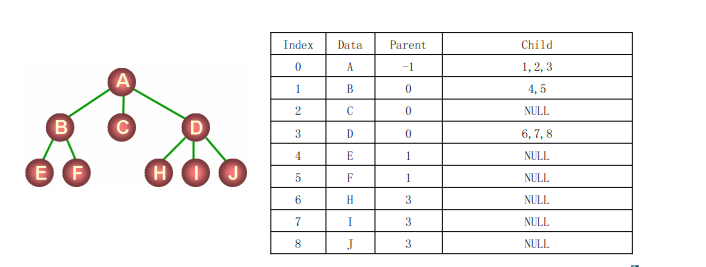
- 无法直接用数组表示树的逻辑结构
- 但可以设计结构体数组对结点间的关系进行表述
例如:
5、实现方案
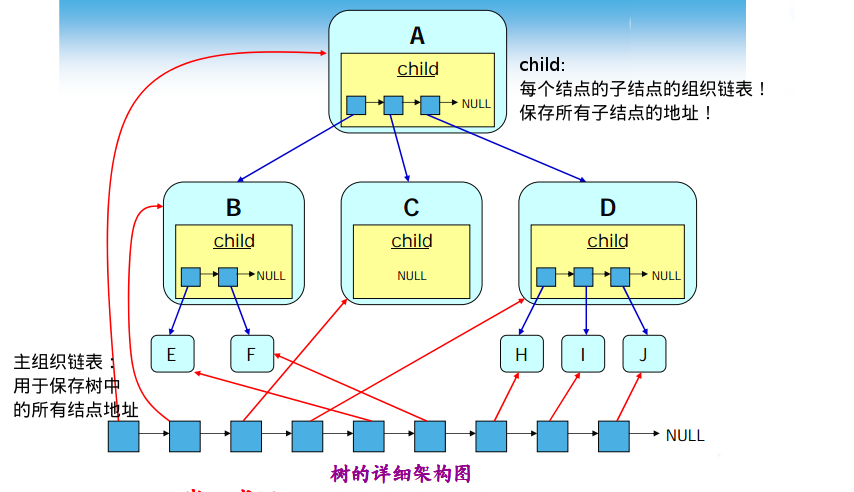
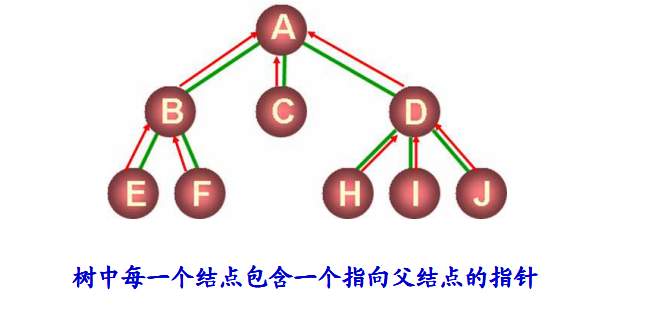
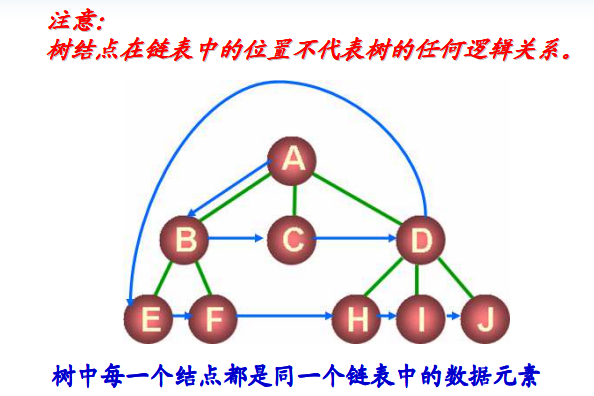
- 利用链表组织树中的各个结点
- 链表中的前后关系不代表结点间的逻辑关系
- 结点的逻辑关系由child数据域描述
- child数据域保存其他结点的存储地址
数据结构的定义:
对外的数据定义:
//gtree.h
//对外的数据封装,增加程序的通用性
typedef void GTree;
typedef void GTreeData;内部实现的数据定义:
//gtree.c
//树结点定义
typedef struct _struct_gtreenode GTreeNode;
/*
data: 指向树中保存的用户数据地址
parent:指向该结点的父结点
child:该结点的子结点组织链表
*/
struct _struct_gtreenode
{
GTreeData *data;
GTreeNode *parent;
Linklist *child;
};
//组织链表结点定义
typedef struct _struct_tlnode TLNode;
/*
listNode: 链表结点,包含指向下一个结点的指针
node:保存树结点地址
*/
struct _struct_tlnode
{
LinklistNode listNode;
GTreeNode *node;
};6、部分代码
/*
将结点node插入到GTree中的pos位置处
插入成功,返回1,失败,返回0
*/
int GTree_Insert(GTree* tree, GTreeData* data, int parentpos)
{
int iret = 1;
iret = iret && (tree != NULL) && (data != NULL) && (parentpos <= List_Length(tree));
if(iret)
{
GTreeNode *treeNode = (GTreeNode*)malloc(sizeof(GTreeNode));
//创建主组织结点,并插入主组织链表中
TLNode *tlNode = (TLNode*)malloc(sizeof(TLNode));
iret =(treeNode != NULL) && (tlNode != NULL);
if(iret)
{
treeNode->data = data;
treeNode->parent = NULL;//假设当前结点没有父结点也没有子结点
treeNode->child = NULL;
tlNode->node = treeNode;
iret = List_Insert(tree,(LinklistNode*)tlNode,List_Length(tree));
//如果未插入成功,则可释放内存
if(!iret)
{
free(tlNode);
}
//尝试获取当前结点的父结点
TLNode *parentNode = (TLNode*)List_Get(tree,parentpos);
if(parentNode != NULL)
{
//如果有父结点存在,将当前结点,插入父结点的子结点的组织结构链表中
treeNode->parent = parentNode->node;
//如果父结点的组织结构链表为空,则先创建它
if(parentNode->node->child == NULL)
{
parentNode->node->child = List_Create();
}
TLNode *pchildNode = (TLNode*)malloc(sizeof(TLNode));
//如果这里条件判断失败,也有可能是上面的插入操作失败造成的
iret = iret && (pchildNode != NULL) && (parentNode->node->child != NULL);
if(iret)
{
pchildNode->node = treeNode;
iret = List_Insert(parentNode->node->child,(LinklistNode*)pchildNode,
List_Length(parentNode->node->child));
}
//如果未插入成功,则可释放内存
if(!iret)
{
free(pchildNode);
}
}
}
else
{
free(tlNode);
free(treeNode);
}
}
return iret;
}/*
递归函数
核心思想是:要删除一个结点,递归删除它和它的所有子结点
*/
static void recursivr_delete(GTree *tree,GTreeNode *node)
{
if((tree != NULL) && (node != NULL))
{
//把它从主组织链表中删除
for(int i = 0; i < List_Length(tree); i++)
{
TLNode *tlNode = (TLNode*)List_Get(tree,i);
if ((tlNode != NULL) && (tlNode->node == node))
{
List_Delete(tree,i);
free(tlNode);
break;
}
}
//如果它有父结点,把它从它的父结点中的子结点组织链表中删除
GTreeNode *parentNode = node->parent;
if(parentNode != NULL)
{
for(int i = 0; i<List_Length(parentNode->child); i++)
{
TLNode *childNode = (TLNode*)List_Get(parentNode->child,i);
if(childNode->node == node)
{
List_Delete(parentNode->child,i);
free(childNode);
break;
}
}
}
//如果它有子结点,递归删除它所有的子结点
if(node->child != NULL)
{
for(int i = 0; i < List_Length(node->child); i++)
{
TLNode *childNode = (TLNode*)List_Get(node->child,i);
if(childNode != NULL)
{
recursivr_delete(node->child,childNode->node);
}
}
}
free(node);
}
}
/*
将GTree中pos位置的结点删除并返回其中的数据
删除成功,返回结点中的数据指针,失败,返回NULL
*/
GTreeData* GTree_Delete(GTree* tree, int pos)
{
GTreeData *ret = NULL;
TLNode *treeNode = (TLNode*)List_Get(tree,pos);
if(treeNode != NULL)
{
ret = treeNode->node->data;
recursivr_delete(tree,treeNode->node);
}
return ret;
}/*
递归函数
求树的高度,将问题转化为求一个结点的子结点高度,如此递归
*/
static int recursivr_height(GTree *tree,GTreeNode *node)
{
int iret = 0;
if((tree != NULL) && (node != NULL))
{
int subHeight = 0;
//获取当前结点的所有子节点
for(int i = 0; i < List_Length(node->child); i++)
{
TLNode *childNode = (TLNode*)List_Get(node->child,i);
if(childNode != NULL)
{
//递归,获取子节点的高度
subHeight = recursivr_height(tree,childNode->node);
}
if(iret < subHeight)
{
iret = subHeight;
}
}
//加上自己的高度1
iret = iret + 1;
}
return iret;
}
/*
返回GTree的高度
如果成功,返回非负值,否则返回-1
*/
int GTree_Height(GTree* tree)
{
int iret = -1;
TLNode *root = (TLNode*)List_Get(tree,0);
if(root != NULL)
{
iret = recursivr_height(tree,root->node);
}
return iret;
}/*
递归调用
求树的度,问题转化为求每个子节点的度,取最大值
*/
static int recursivr_degree(GTreeNode *node)
{
int iret = 0;
if(node != NULL)
{
int subDegree = 0;
//获取当前结点子结点数目
iret = List_Length(node->child);
//获取当前结点,所有子结点的度
for(int i = 0; i < List_Length(node->child); i++)
{
TLNode *childNode = (TLNode*)List_Get(node->child,i);
if(childNode != NULL)
{
subDegree = recursivr_degree(childNode->node);
}
//取最大值,最为当前结点的度
if(iret < subDegree)
{
iret = subDegree;
}
}
}
return iret;
}
/*
返回树的度数
如果成功,返回非负值,失败,返回-1
*/
int GTree_Degree(GTree* tree)
{
int iret = -1;
TLNode *root = (TLNode*)List_Get(tree,0);
if(root != NULL)
{
iret = recursivr_degree(root->node);
}
return iret;
}/*
递归调用,显示当前结点的值,及其所有子结点的值
*/
static void recursivr_display(GTreeNode *node,GTree_Printf pfunc, int subindex, char div,int gap)
{
if(node != NULL)
{
for(int i = 0; i < subindex; i++)
{
printf("%c",div);
}
//回调函数
pfunc(node->data);
if(node->child != NULL)
{
for(int i = 0; i < List_Length(node->child); i++)
{
TLNode *childNode = (TLNode*)List_Get(node->child,i);
if(childNode != NULL)
{
recursivr_display(childNode->node,pfunc,subindex + gap,div,gap);
}
}
}
}
}
/*
显示树的结构和内容
tree:树的指针
pfunc:毁掉函数指针,由用户自行编写
div:自定义分割符
gap:自定义间隔
*/
void GTree_Display(GTree* tree, GTree_Printf pfunc, char div,int gap)
{
TLNode *root = (TLNode*)List_Get(tree,0);
if(root != NULL)
{
recursivr_display(root->node,pfunc,0,div,gap);
}
}7、完整源码下载
文件名:gtree-1.0.tar.gz
链接: http://pan.baidu.com/s/1o6OLhYq 密码: tew8
编译步骤:
0.1 解压缩:tar -zxvf gtree-1.0.tar.gz
0.2 进入目录:./configure
0.3 生成Seqlist:make
0.4 运行程序:./GTree
























 269
269

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








