机器学习之-搞定支持向量机（SVM）【人工智能工程师--AI转型必修课】

一听到支持向量机这个名字，给大家的感觉应该是这个样子滴，感觉好像很高端一个事情，但是又不知道它到底在什么。咱们今天的目标就是用最通俗的语言搞定它！

首先我们来看一下咱们的支持向量机是要打算干一个什么大事情！其实我第一次听到这个名字的时候最想搞清楚的就是它为啥起了个这么个怪名字（看完你就懂啦）！对于一个分类任务而言，最主要的目标就是能分得开，但是对于上图当中的两类数据点来说，我可以找到三条线把它们都完全分得开，其实可以找到无数条的！那么问题也随之而来了，到底选谁呀？第二点，如果数据本身就很复杂，我们的这个线性分类还够用吗？第三点，这么强大的一个算法，它的计算复杂度咋样呀？这些就是我们现在面临的问题，准备逐一攻克吧！

这里放上两张图，看起来有啥区别呢？左边的决策的区域感觉小一些，右边的大一些！但是他们俩是不是都完成了一个任务呀，完全把数据点切分开了！这个事咱可以这么唠，左右两边现在不是数据点了而是交战双方的雷区，想想战狼2最后是不是从两个交战区域冲出来了！

两边都是雷区，我们现在要开辟出来一条隔离带，既不能碰到任何一个雷，还得让我们的大部分安全通过，那这条隔离带你说左边的好还是右边的好呢？必然是右边的吧，因为更胖一些，这样我们的部分更安全，说白了我们要的决策边界应该泛化能力更强一些的！

既然说到雷了，最起码的一个要求就是不能碰到它呀！那么我们来想，你要是碰到雷应该先碰哪个呀？离你隔离带最近的那个吧，那这里我们就得说说距离这个问题了，它决定了雷是你咱们隔离带多远的！

假设我们的隔离带就是这个平面，有一个雷X，那么现在咱们来算一下这个雷到我平面的距离有多远！直接算感觉好像有点难，咱们来转换一下，这里假定平面上有两个点X’和X”,如果我知道X到X’的距离，然后把这个距离投影到我的垂线方向，这样不就间接的计算出雷X到平面的距离了嘛。平面的垂线方向又恰好是它的法向量，只需求出它的单位向量就可以啦！问题迎刃而解，这样就有了一个雷到隔离带的距离了！

接下来对我的数据集进行如下定义，支持向量机是一个经典的二分类问题，在这里我们认为如果说一个点就是一个正例，那么对应的标签值就是+1，如果一个点是负例，那么对应的标签值就是-1。对应于我的决策方程，就可以做这样的定义啦，如果预测值Y(x)>0我就说它是一个正例，如果 Y(x)<0我就说它是一个负例。两个式子看起来有点多，整合一下吧，既然>0的时候标签值为+1,<0的时候标签值为-1。那么它们的乘积就必然是恒大于0的啦！

下面咱们来看一下我们要优化的目标是啥呢？我现在是不是要找最好的一个隔离带（也就是决策方程，说白了就是w和b）！这个隔离带要能够尽可能的安全，所以就要使得离它最近的那个雷（先会碰到最近的）越远越好呀！只要大家能理解这句话，支持向量机也就差不多有个意思了！在看点到决策边界的距离，原始的式子中有个绝对值，现在我们展开是不是也可以呀，因为y*y(x)恒正嘛！

来看我们要优化的目标，这个一个求最小，完了又求最大，这个啥意思啊？想想咱们的隔离带咋说的，是不是先求最近的雷，然后让这个雷滚的越远越好呀！这就是我们最小和最大是啥意思！但是现在这个式子看起来有点复杂呀，能不能简化一下呀，直接我们认为y(x)恒大于0，现在咱们把这个条件放的宽松一些，总可以通过放缩变换让y(x)>=1嘛，这样问题就简单了！既然要求y*y（x）的最小值，现在是不是最小值就是1呀，这样这个式子不久能化简掉了嘛！

下面咱们来看，只剩下求解一个最大值啦！但是我们的常规套路是不是把一个最大值问题转换成一个最小值问题呀，直接求它倒数的最小值不久完了嘛！那这个带有约束条件的极值问题该怎么求呢？自然想到了一个神器：拉格朗日乘子法。这个概念如果没接触咱们就这么唠，现在我的目标是找到最合适的W和B但是这样还带约束的条件看起来比较难，所以我们想把这样一个问题转换成一个求解容易些的中间值问题，这个中间值能够和W还有B扯上关系，这样求出来了中间值就能找出来W和B了，差不多就是这个意思！

这个式子就是我们标准的拉格朗日乘子法嘛，感兴趣可以翻翻咱们的高数书来回顾下，估计你们也不感兴趣，那就认为科学及推导出来的东西是对的就好啦！

这里我们利用了对偶条件，啥意思呢？看起来就是最大最小调换了一下，其实这是一个证明，可以参考下拉格朗日KKT条件，这个说起来就太恶心人了，感兴趣看看KKT这三个科学家干了一件什么事吧！
接下来我就要先求解什么样的w和b能够使得当前的L式子的值最小吧！这个我们自然想到了直接求偏导嘛！分别对w和b求偏导，然后得到了上述式子。
将得到的解带回到原式当中，相当于把w和b就约分掉了，那么我们现在要求解的就是什么样的a值，能够使得这个式子最大吧！
对要求的极大值式子同样加上了相反数变换成了求极小值的问题，到这里已经接近我们最终的答案啦！
来看一个小例子吧，这个只是举例来说SVM怎么求解，真正的求解方式参考SMO算法吧！这里我们有三个数据点，2个正例，1个负例，通过它们要得到最好的决策方程！在约束条件中，就要把之前所考虑的条件都带上啦，拉格朗日乘子法也有自身的约束条件就是所有的a值必须都大于0.
对于这样的式子，将我们的数据全部带入就好了，注意一点，这个x之间求的是内积！
在求极值的过程中，我们直接对a1和a2求偏导得到了结果，但是发现结果却不满足我们的约束条件，这怎么办呢？既然极值点不满足，我们只能在边界上来寻找了！
在边界上我们求出来所有的a值，这样是不是就完成啦求解的任务呀！因为我们知道a和w之间的关系呀，再继续求解就能够算出来w和b啦，到此我们就求解出来了这个问题的解有了决策边界！

回过头来想一想，对于a值来说，是不是有些算出来是一个数，有些算出来就是0呀，咱们的a2就是0呀，回到那3个点的图中看一下，发现什么了？2号样本点是不是非边界上的点呀，那咱们来想它的a值等于0，那么最终的w在计算的时候是不是就跟它无关了呀，那么在这里我们得出了一个非常重要的结论，支持向量机是由边界上的点所支撑起来的（因为边界上的点的a值不为0，非边界上的点的a值为0呀），那么我们就把边界上的点叫做支持向量！现在知道支持向量机这个奇怪的名字咋来的了吧！
这里做了这样一个实验，保证边界上的点不变，然后在数据集中增加数据，发现了一个事，决策边界没有发生变化！左边是60个数据的右边是120个的，只要支持向量没变，边界就不会变，这就是支持向量机，因为再加的点a值都为0呀！

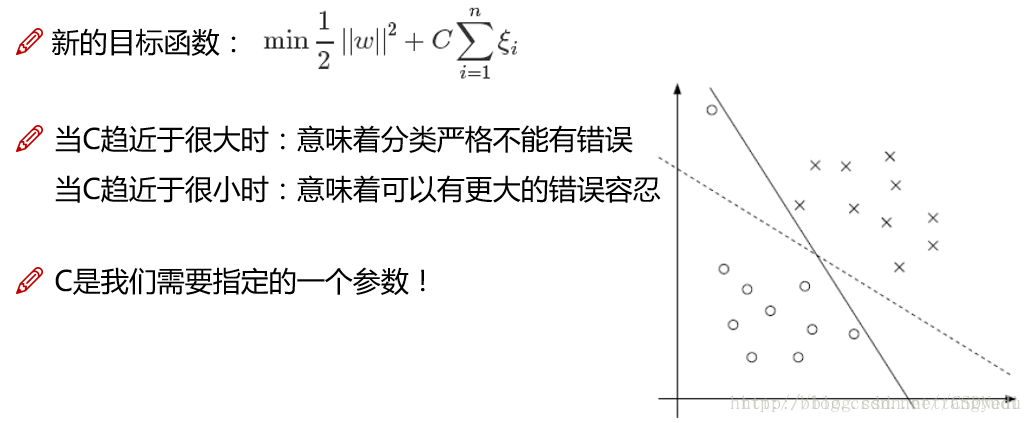
新问题又来啦！在这里我们发现了一个事，在构建决策边界的过程中，如果某一个点比较特(离群点)，我们的边界会为了满足它而把隔离带做的很小，这该咋办呀？让我们的决策边界要求放低一些吧！
由于之前的要求太严格了，在这里我们指定了一个新的东西叫做松弛因子，在目标函数中把它考虑进来了，啥意思呢？来看一下吧，引入了参数C相当于松弛因子让咱们决策边界放松的大小！如果C很大，那我们还想让目标函数很小，是不是松弛因子就得很小了吧！如果C很小呢？那么松弛因子稍微大一些也没关系吧！就是这个意思！

又一个问题来啦，现在我的数据复杂起来了，在低维中很难进行区分，这该怎么办呢？一个最简单的想法就是把数据映射到高维空间，这样特征信息就更多了，决策边界就更容易建立出来了吧！

这里我们要做的就是找到一种变换的方法，将数据的特征进行高维的映射，但是问题也来了，这样的计算复杂度是不是也上来了呀！其实是这个样子的SVM在数学上有这样一个巧合，我们可以把高维特征的内积在低维当中直接计算好然后做映射也是一样，恰好解决计算的问题！

这个就是线性的和经过核函数特征变换后的结果，怎么样，SVM确实蛮厉害的吧！这些就是咱们支持向量机的推导啦，感谢各位观众老爷们的收看！机器学习故事汇-搞定支持向量机（SVM）

机器学习30天系统掌握【升级】

讲师介绍：
唐宇迪，计算机博士，专注于机器学习与计算机视觉领域，深度学习领域一线实战专家，善于实现包括人脸识别，物体识别，关键点检测等多种应用的最新算法。参与多个国家级计算机视觉项目，多年数据领域培训经验，丰富的教学讲解经验，出品多套机器学习与深度学习系列课程，课程生动形象，风格通俗易懂。

课程介绍：
这将是你成为机器学习工程师的最佳实践指南，通过30天实训，层层递进，彻底掌握机器学习！
知识系统性归纳+实时答疑+源码共享+案例实战，五大模块的支撑，这才是从零入门的正确打开方式！课程分为四个阶段：基础讲解+算法进阶+案例实战+行业应用。全程采用案例实战，为快速与实际项目接轨打定基础！
课程从机器学习经典算法的数学原理推导与实例讲解，通过原理分析，通俗解读，案例实战让大家快速掌握机器学习经典算法原理推导与工作流程，掌握Python数据分析与建模库使用方法，从案例角度思考如何应用及其学习算法解决实际问题。

目标人群：
1. 适合零基础！对机器学习感兴趣，或致力于从事人工智能领域的开发者！
2. N+知识点+手把手掌握+源码共享+实时答疑，系统性学习与消化！
3. 全程案例实战，从案例中学习，事半功倍！报名就赠：Python机器学习必备库！全程金牌辅导！

课程特色：
专属答疑+课件资料提供+视频无限时回放+VIP交流群

开课时间：
随到随学，自由支配

点我试看： http://edu.csdn.net/course/detail/6108?utm_source=blog11