- 论文标题:Submanifold Sparse Convolutional Networks
- 中文标题:子流形稀疏卷积网络
- 论文下载地址:arxiv@1706.01307
- 论文项目地址:GitHub@SparseConvNet,注意该项目是基于 P y T o r c h \rm PyTorch PyTorch开发的,是一个可安装的 P y t h o n P a c k a g e \rm Python\space Package Python Package,且只能在 L i n u x \rm Linux Linux环境中安装,目前该 P a c k a g e \rm Package Package还没有被 P y P i \rm PyPi PyPi收录,各大镜像上也搜不到这个包(
spconv)。
序言
之所以距离 D D L \rm DDL DDL还剩四五天还重看一篇论文,是因为上一篇【论文实现】以SVD的分解形式进行深度神经网络的训练(PyTorch)出现很严重的问题,似乎对稀疏训练的理解还是太浅薄,毕竟已经有前人对稀疏训练做了一些工作的,可以考虑借鉴一些内容。本文应该算是比较有深度的一篇文章了,因为作者完成了全部的实现并封装成包。
纵观这学期,从寒假伤病的低谷中慢慢休整,直到三月中旬跑出第一个 45 45 45分以内的 10 k m 10\rm km 10km宣告恢复巅峰,后来四月到五月经历了一场过山车式的恋爱,尝尽酸甜苦辣。五月潜心跑步,在繁忙的学业中完成月跑 135 k m 135\rm km 135km,数次刷新 p b \rm pb pb并完成寒假时就想跑的人生第一个场地半马。最终在 6 6 6月 19 19 19日把 10 k m 10\rm km 10km跑到历史最佳 42 42 42分 33 33 33秒,此时笔者也从期初的近 78 k g 78\rm kg 78kg掉到只剩 66 k g 66\rm kg 66kg,可能是近十年以来最轻的体重了。
整体来看,这学期对笔者的影响特别特别的大,除了跑步及其带来的改变外,笔者与两三位挚友的深交,也加深了对一些人和许多事的认识与经验。虽然在很多方面依然还是非常非常的菜,毫无任何长进,那笔者也无可奈何了。
说说最近的事情,期末考成狗,成绩还没全部出来,估计不会特别好看。这两天在赶邓琪最终的汇报,搞完基本上这学期就彻底解脱了。又一学期结束,发现依然两手空空,实在是非常的真实。近期身体状态一般(天气太热,真的跑不动),学习状态尚可(受了一些刺激)。虽然已经过了很久,心态很平复了,但是偶尔还是会被一些突发事件给触动。虽说眼不见为净,但是好奇心总会害死猫,尤其当 W \rm W W的 P O S T \rm POST POST莫名其妙就出现在了列表里时,事情就变得非常胃疼。
人生也可以视为一个不断适应变化的过程罢,可能笔者之前的生活过于一成不变了,约莫如是,毕竟完全极端地抹除一些存在几乎是不可能的。
目录
- 序言
- 摘要 Abstract \text{Abstract} Abstract
- 1 1 1 引入 Introduction \text{Introduction} Introduction
- 2 2 2 动机 Motivation \text{Motivation} Motivation
- 3 3 3 稀疏卷积层与合理的稀疏卷积层 SC and VSC \text{SC and VSC} SC and VSC
- 4 4 4 实现 Implementation \text{Implementation} Implementation
- 5 5 5 实验 Experiments \text{Experiments} Experiments
- 6 6 6 相关工作 Related Work \text{Related Work} Related Work
- 7 7 7 结论 Conclusion \text{Conclusion} Conclusion
- 参考文献 References \text{References} References
- 图表汇总
摘要 Abstract \text{Abstract} Abstract
-
卷积神经网络(convolutional neural networks,下简称为 CNN \text{CNN} CNN)通常用于分析时空数据(spatio-temporal data),如图像、视频、 3 D \rm 3D 3D图形等。这类数据的张量表示一般是稠密的(dense),但是也有稀疏的(sparse)情况,如:
- 白纸上的笔画(penstrokes),本质是在二维白纸上用一维黑笔进行涂鸦,得到的图片矩阵是稀疏的,同理通过 O F F \rm OFF OFF模型在 3 D 3\text{D} 3D空间中构造 2 D 2\text{D} 2D平面得到的 3 D 3\rm D 3D张量也是稀疏的。
- 通过 LiDAR \text{LiDAR} LiDAR扫描仪或者 RGB-D \text{RGB-D} RGB-D照相机拍摄得到的 3D \text{3D} 3D点云(point clouds);
一般来说常规针对稠密张量的运算方法在稀疏张量上是低效的,同理 CNN \text{CNN} CNN的传统实现算法在稀疏输入数据上的运算也是很低效的。
-
本文实现一种用于处理稀疏输入的 CNN \text{CNN} CNN,与以往工作的不同之处在于,本文的实现方式的 CNN \text{CNN} CNN严格地在子流形上实现运算(operates strictly on submanifolds),而非在网络中的每一层进行扩张观测(dialting the observation with every layer in the network)。
原文:
We introduce a sparse convolutional operation tailored to processing sparse data that differs from prior work on sparse convolutional networks in that it operates strictly on submanifolds, rather than ‘dilating’ the observation with every layer in the network.
- 笔者注:
关于何为子流形,何为扩张观测,仍需后文的阅读与理解。- 子流形:指高维空间中的低维数据。
- 扩张观测:目前的理解是对于扩张的理解是卷积层中的非基态元素会在前向传播中以指数级的速度扩张成更多的非基态元素,非基态元素的运算相比于基态元素要慢,所以会导致原本稀疏的输入不断变稠密,导致运行复杂度增加。
- 笔者注:
-
本文的实验结果表明,子流形稀疏卷积网络(submanifold sparse convolutional networks,下简称为 SSCN \text{SSCN} SSCN)可以在显著较少的计算量下取得与先进的模型基本同等水平的结果。
1 1 1 引入 Introduction \text{Introduction} Introduction
-
正如摘要提及的那样,一些时空数据的张量表示是稀疏的,而传统 CNN \text{CNN} CNN处理稀疏输入非常低效,因此前人已经实现了一些用于高效处理稀疏输入的 C N N \rm CNN CNN架构:
-
参考文献 [ 1 ] [1] [1]:与传统 CNN \text{CNN} CNN实现并无大异,但是在每秒浮点运算数(floating point operation per second,下简称为 FLOPs \text{FLOPs} FLOPs)层面上改进了计算资源的耗用。
-
参考文献 [ 2 ] [2] [2]:与传统 CNN \text{CNN} CNN实现并无大异,但是改善了内存占用。
-
参考文献 [ 9 ] [9] [9]:该文提出 O c t N e t s \rm OctNets OctNets微调了卷积算子(convolutional operator)来生成那些原理兴趣区域(regions of interest)的网格点(grid)中的平均隐层状态(average hidden states)。
-
笔者注:这个可能需要阅读原论文才能弄明白究竟 O c t N e t s \rm OctNets OctNets做了什么,看起来参考文献 [ 9 ] [9] [9]还是比较新的论文( 2016 2016 2016),应该还是值得一看的,看标题似乎是关于高维表示的学习,笔者猜想可能是通过对高维稀疏数据进行嵌入降维来降低复杂度。
在本文第 6 6 6节相关研究中专门对参考文献 [ 9 ] [9] [9]做了一些描述,可以看一看。
-
-
-
上述三篇参考文献的缺陷在于,它们把稀疏数据在每一层都进行了扩张(dilate),因为他们实现了一个完整的(full)卷积函数。而本文实现了贯穿整个网络的运算过程中,可以保持相同的稀疏模式(sparsity pattern)来训练 C N N \rm CNN CNN,而无需扩张特征映射(feature maps)。
-
笔者注:
- 特征映射(feature maps),或者翻译为特征图,是 C N N \rm CNN CNN中的重要概念,每个卷积层会计算 o u t c h a n n e l s \rm outchannels outchannels张特征图,然后将这些特征图叠加得到卷积层的输出结果。
- ~~其实这句话还是很难于理解,仍需下文的阅读与理解。~~基本算是搞明白了。
-
-
本文具体实现方法是提出两种卷积算子(convolutional operator):详见本文第 3 3 3节相关内容
- 稀疏卷积层(sparse convolution,下简称为 S C \rm SC SC);
- 合理的稀疏卷积层(valid sparse convolution,下简称为 V S C \rm VSC VSC);
-
本文的实验是基于手写数字识别与 3 D 3\rm D 3D图形状的数据集,实验结果显示在保持先进模型性能的基础上,可以减少 50 % 50\% 50%的算力与内存开销。
2 2 2 动机 Motivation \text{Motivation} Motivation
-
定义 2.1 2.1 2.1:称一个 C N N \rm CNN CNN是 d d d维的,若它的输入张量是 d + 1 d+1 d+1维的,其中包含 d d d维的时空维度(spatio-temporal dimensions),如长、宽、高、时间戳等,以及 1 1 1维的特征空间维度(feature space dimensions),如 R G B \rm RGB RGB图像的通道(channels)、曲面法向量(surface normal vector)等。
-
定义 2.2 2.2 2.2:每个稀疏输入对应一个与特征向量(feature vector)相联系的 d d d维站点网格(grid of sites)。称输入张量中的一个站点(site)是活跃的(active),若与之相联系的特征向量中的任意元素都不处于基态(ground state),比如特征向量中的任意元素都非零。
在实际操作中一般会设置阈值来消除那些距离基态很近的站点。
注意:虽然输入张量是 d + 1 d+1 d+1维的,但是活跃性(activity)是一种 d d d维性质,即沿特征空间维度的整个平面要么是活跃的,要么是非活跃的。
-
定义 2.3 2.3 2.3: CNN \text{CNN} CNN的隐层也可以用一个 d d d维特征空间向量网格(grids of feature-space vectors)来表示。当输入张量在网络中进行运算时,称隐层中的站点是活跃的,若该层中的任意被当作输入的站点都是活跃的。
… a site in a hidden layer is active if any of the sites in the layer that it takes as input is active.
比如我们使用 3 × 3 3\times3 3×3的卷积核,则每个站点都与隐层中的 3 × 3 = 9 3\times3=9 3×3=9个站点连接。
-
定义 2.4 2.4 2.4:隐层的活跃性定义也可以类似归纳得到,即每层可以确定下一层中所有活跃状态(active state)。在每个隐层中,不活跃的站点都具有相同的特征向量,即特征向量中所有元素处于基态。注意隐层中的基态通常不为零,尤其是卷积层是带有截距项(bias)时。
- 笔者注:意思应该是基态就是截距项的向量,可能可以理解为基态就是输入为全零时的输出结果。
然而不论基态的具体数值如何,计算出基态的具体数值都只需要在模型训练时进行一次前向传播即可,这就意味着可以显著地节省运行时间与内存占用,具体节省情况依赖于数据稀疏度与网络深度。
-
本文认为上述的架构是不适当的,因为卷积运算并没有调整成适应输入数据的稀疏性。若输入数据包含单一的活跃站点(single active site),则采用 3 d 3^d 3d次卷积后,将会有 3 d 3^d 3d个活跃站点;如果进行第二次卷积操作则会生成 5 d 5^d 5d个活跃站点,依此类推,这在需要进行成百上千次卷积的 C N N \rm CNN CNN网络(如 V G G , R e s N e t s , D e n s e N e t s \rm VGG,ResNets,DenseNets VGG,ResNets,DenseNets,对应参考文献 [ 3 , 4 , 10 ] [3,4,10] [3,4,10])中是非常低效的。
当然 C N N \rm CNN CNN一般不会接收只有单一的活跃站点的输入张量,但是上述的扩张(dilation)问题仍然会在摘要中提及的一些稀疏数据上发生(即高维输入张量上只有低维的数据非零)。
-
为了强调活跃站点的扩张问题,本文提出两个稍有不同的卷积运算(即 S C \rm SC SC和 V S C \rm VSC VSC),这两种卷积运算都忽略了基态——它们将基态直接用零向量替代,从而简化了卷积操作。
两者的区别在于它们处理活跃站点的方式,之前的扩张问题是源于,如果有一个输入站点是活跃的,则输出的站点活跃,改进后的卷积运算只考虑中心输入(central input),于是输入站点的活跃情况与输入站点的活跃情况基本相似。
-
笔者注:
到这里可能很多人不是搞得很明白作者究竟想要做什么(一堆乱七八糟的定义),笔者大致梳理一下:
- 其实关于上面的扩张还是比较容易理解的,因为相当于卷积核是一个窗口,窗口里只要有一个活跃站点,就意味着这次输出的结果是活跃的,因此考虑一个 2 D 2\rm D 2D卷积层, 3 × 3 3\times 3 3×3的卷积核在单一的活跃站点上就会输出成 9 9 9个活跃站点(步长为 1 1 1的移动窗口),在到下一层就是 5 × 5 = 25 5\times 5=25 5×5=25个。所谓站点可以应该理解为一个二维图像上的一个像素点,三维图像(带 c h a n n e l \rm channel channel)上一个像素点的一个通道值等。
- 因此 C N N \rm CNN CNN的问题就是即便输入数据很稀疏,但是经过两三个卷积层之后就会变得非常稠密,这在下面的 Figure 1 \text{Figure 1} Figure 1中可以很清楚地看到。
- 现在不太容易搞得很清楚的可能是基态的具体定义与性质(上面我认为基态指输入为全零张量的输入,即输入的是非活跃的情况下的输出结果),以及为什么基态会很容易计算。
- 这部分可能需要重新回顾以下 C N N \rm CNN CNN的详细原理,笔者刚好前一阵子重写低秩分解 C N N \rm CNN CNN模块时回顾过了,所以相对理解得要快一些,看到这里觉得本文有些意思,继续看咯。
2.1 2.1 2.1 子流形扩张 Submanifold Dilation \text{Submanifold Dilation} Submanifold Dilation

-
如 Figure 1 \text{Figure 1} Figure 1所示,这是一个二维网格上的一维曲线示例。即便在该网格图上采用很小的卷积核(如 3 × 3 3\times 3 3×3的卷积核),图像的稀疏性很快就会丢失(从左到右图像显得越来越稠密)。但是如果限制卷积核只输出那些活跃的输入点,隐层就无法捕获到与该一维曲线分类相关的充分信息(比如一维曲线上相邻接的元素可能会被分开考察)。
不过目前大部分 C N N \rm CNN CNN都使用池化(pooling)策略以及带非 1 1 1步长(stride)的卷积核窗口移动策略,这对于处理稀疏输入是很有帮助的,因为它们本质都是合并邻接的输入点的信息。一般来说这些相邻接的元素靠得越近,要求池化窗口大小与卷积核移动步长要更小。
2.2 2.2 2.2 极深的卷积网络 Very Deep Convolutional Networks \text{Very Deep Convolutional Networks} Very Deep Convolutional Networks
- 在常见的图像分类问题中,极深的 C N N \rm CNN CNN一半都带有很小的过滤器(filter,卷积核由 o u t c h a n n e l s \rm outchannels outchannels个过滤器构成),一般是 3 × 3 3\times3 3×3的大小,以及会对原图做 p a d d i n g = 1 \rm padding=1 padding=1的零填充(用于保持特征图的尺寸与原图像同等),这种做法已经被证明是非常有效的,如在 V G G \rm VGG VGG中有很良好的应用。
-
R
e
s
N
e
t
s
\rm ResNets
ResNets的成功表明又深又窄且带有小过滤器的网络是很高效的,因为这样每次都只需要计算很少量的特征,然后只需要将这些特征合并就可以得到一个非常大的状态变量(state variable)。
- 笔者注:过滤器越小意味着卷积层参数共享程度越高,因为全连接层本质上是过滤器大小与输入同等大小的卷积层的特例。本文似乎不怎么区分过滤器与卷积核两者的说法,其实这两个概念也没有太大区别,后者由若干前者叠置构成。
- 不幸的是,这些技术都不适用于现存的稀疏
C
N
N
\rm CNN
CNN代码实现,一个问题是带有多条路径的网络倾向于生成不同的活跃路径(active paths),这些活跃路径需要合并以重新连接各个输出,而这样的合并是很难高效做到的。尤其是在
R
e
s
N
e
t
s
\rm ResNets
ResNets以及
D
e
n
s
e
N
e
t
s
\rm DenseNets
DenseNets这些大模型中,输入数据的稀疏性很容易就被破坏,活跃站点的数量会爆炸式地增长。
- 笔者注:多条路径的意思不是很明白,可能是网络中带有很多分支?似乎不是很重要的概念。
3 3 3 稀疏卷积层与合理的稀疏卷积层 SC and VSC \text{SC and VSC} SC and VSC
-
定义 3.1 3.1 3.1:定义稀疏卷积层 SC ( m , n , f , s ) \text{SC}(m,n,f,s) SC(m,n,f,s),其中:
- m m m为输入特征平面(input feature planes)的数量;
- n n n为输出特征平面(output feature planes)的数量;
-
f
f
f为过滤器的尺寸,假定为奇数,但是允许过滤器不是正方形的,如
f
=
3
×
5
f=3\times5
f=3×5或
f
=
5
×
3
f=5\times3
f=5×3,这样可以实现
Inception-style factorised convolution
\text{Inception-style factorised convolution}
Inception-style factorised convolution(参考文献
[
11
]
[11]
[11]);
- 笔者注:笔者不是很了解 C N N \rm CNN CNN中 I n c e p t i o n \rm Inception Inception的概念,不过这应该是一个很重要的概念。大致的意思应该是把大过滤器分解为多个小的过滤器,比如现在 G o o g l e N e t \rm GoogleNet GoogleNet用大小为 1 × 1 1\times 1 1×1的过滤器,做到既可以保持网络的稀疏连接以及硬件上对于矩阵运算的优势。详细可以参考zhihu@深度学习20讲CNN之GoogLeNet Inception。
- s s s为步长,也假定为奇数,这里没有说各个维度上步长可以不相等。
-
SC \text{SC} SC计算活跃站点的方法与传统卷积层相同:
- 首先在大小为
f
d
f^d
fd的接受域(receptive field)中寻找活跃站点;
- 笔者注:可能有人不清楚接受域是什么,笔者觉得应该就是卷积核框住的那一块 3 × 3 3\times 3 3×3的位置。
- 若输入大小为 l l l,则输出的大小为 l − f + s s \frac{l-f+s}s sl−f+s;
S C \rm SC SC与传统卷积层不同之处在于,它直接不考虑非活跃站点的基态,因为 S C \rm SC SC假设从这些站点的输入就是零。看起来这只是很小的改变,但是实际上就是可以大大提升计算效率。
- 笔者注:笔者觉得是不是就是很浅显的一个事实,在卷积层运算中,只需要考虑稀疏张量中那些非零的元素即可,其他地方都不考虑,直接输出成基态值即可。后面如果有新的理解,再来更新这里的笔注。
接下来这个 V S C \rm VSC VSC就比较复杂了,也是本文的主要贡献,注意所用标记( m , n , f , s m,n,f,s m,n,f,s)同上。
- 首先在大小为
f
d
f^d
fd的接受域(receptive field)中寻找活跃站点;
-
定义 3.2 3.2 3.2:合理的稀疏卷积层 VSC ( m , n , f , 1 ) \text{VSC}(m,n,f,1) VSC(m,n,f,1)是 SC ( m , n , f , 1 ) \text{SC}(m,n,f,1) SC(m,n,f,1)的一个变体;
-
首先在输入张量的每边填充(pad) f − 1 2 \frac{f-1}2 2f−1次,从而输出与输入形状保持相同;
-
然后令输出站点是活跃的,当且仅当该输出站点对应的输入站点是活跃的。
-
笔者注:
-
注意因为通过 p a d d i n g \rm padding padding已经使得输入输出同形,因此这里每个输出站点刚好可以对应一个输入站点,这个刚好就是过滤器对应的中心点(这也是为什么 f f f要取奇数,否则就没有中心点了)。
-
不过问题在于可能 i n c h a n n e l s \rm inchannels inchannels与 o u t c h a n n e l s \rm outchannels outchannels的大小不一样的,而且理论上每个输出节点应该在输入上的每个 c h a n n e l \rm channel channel里都有一个对应站点,所以这里其实还是有点表述不清,可能只是考虑 i n c h a n n e l s = o u t c h a n n e l s = 1 \rm inchannels=outchannels=1 inchannels=outchannels=1的情况?继续往下面看罢。
-
-
-
一旦某个输出站点被确定为是活跃的,则它的输出特征向量就可以通过 S C \rm SC SC进行运算。
-
-
Table 1 \text{Table 1} Table 1中展示的是传统卷积层与 S C \rm SC SC和 V S C \rm VSC VSC的运算复杂度对比情况:

-
在对 S C \rm SC SC与 V S C \rm VSC VSC的实际实现过程中,同样需要对应的激活函数(activation functions),批正则化(batch normalization),以及池化函数:
- 激活函数大同小异,不过只需要针对活跃站点进行激活即可;
- 同样的批正则化也是针对活跃站点;
- 最大池化(max-pooling)
MP
(
f
,
s
)
\text{MP}(f,s)
MP(f,s)与平均池化(average-pooling)
AP
(
f
,
s
)
\text{AP}(f,s)
AP(f,s)被定义为是
SC
(
⋅
,
⋅
,
f
,
s
)
\text{SC}(\cdot,\cdot,f,s)
SC(⋅,⋅,f,s)的变体:
- M P \rm MP MP函数是取零向量与接受域(receptive field)中的输入特征向量之间的最大值(即 R e L U \rm ReLU ReLU激活函数的逻辑)。
- A P \rm AP AP函数计算活跃的输入向量的 s u m \rm sum sum值,再除以 f d f^d fd;
-
本文还定义了一个逆卷积(deconvolution)运算 DC ( ⋅ , ⋅ , f , s ) \text{DC}(\cdot,\cdot,f,s) DC(⋅,⋅,f,s)作为 SC ( ⋅ , ⋅ , f , s ) \text{SC}(\cdot,\cdot,f,s) SC(⋅,⋅,f,s)的逆运算,这个因为输入站点和输出站点一一对应,所以其实是很容易实现的一个运算。
3.1 3.1 3.1 子流形卷积网络 Submanifold Convolutional Networks \text{Submanifold Convolutional Networks} Submanifold Convolutional Networks
-
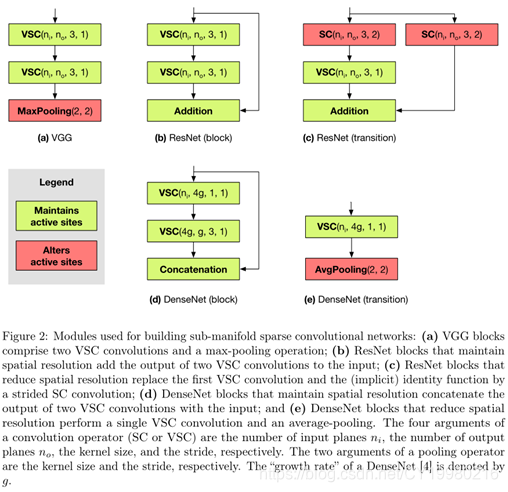
本文结合使用 VSC \text{VSC} VSC卷积层,带步长的(strided) S C \rm SC SC卷积层,以及稀疏池化运算(sparse pooling operations)来构建流行 C N N \rm CNN CNN(如 VGG,ResNet,DenseNet \text{VGG,ResNet,DenseNet} VGG,ResNet,DenseNet)的稀疏版本。
上图 Figure 2 \text{Figure 2} Figure 2展示了本文使用的一些模块构成情况,我们称这样的网络结构为子流形卷积网络( SCN \text{SCN} SCN),因为这种网络结构是专门用于处理高维空间下的低维数据。
-
对 Figure 2 \text{Figure 2} Figure 2的一些简要说明:
-
VGG \text{VGG} VGG:由许多 VSC ( ⋅ , ⋅ , 3 , 1 ) \text{VSC}(\cdot,\cdot,3,1) VSC(⋅,⋅,3,1)构成,中间由最大池化层分隔,每个卷积之后都跟随一个批正则化与 R e L U \rm ReLU ReLU激活函数来引入非线性;
-
pre-activated ResNets \text{pre-activated ResNets} pre-activated ResNets:类似地仍由许多 VSC ( ⋅ , ⋅ , 3 , 1 ) \text{VSC}(\cdot,\cdot,3,1) VSC(⋅,⋅,3,1)构成,其中残差连接(residual connections)都是改为恒等函数(identity functions)。
- 笔者注:恒等函数么?残差连接本质是 F ( x ) = f ( x ) + x F(x)=f(x)+x F(x)=f(x)+x,这里意思是 F ( x ) = x F(x)=x F(x)=x吗?还是就是 F ( x ) = f ( x ) + x F(x)=f(x)+x F(x)=f(x)+x,似乎应该是后者的意思。
一旦输入输出的特征数量不同,将 VSC ( ⋅ , ⋅ , 3 , 1 ) \text{VSC}(\cdot,\cdot,3,1) VSC(⋅,⋅,3,1)改用为 VSC ( ⋅ , ⋅ , 1 , 1 ) \text{VSC}(\cdot,\cdot,1,1) VSC(⋅,⋅,1,1)。
一旦发生规模改变(change of scale),则将第一个卷积核和残差连接替换为 SC ( ⋅ , ⋅ , 3 , 2 ) \text{SC}(·,·,3,2) SC(⋅,⋅,3,2)卷积核,这样确保两个分支可以共用同一个活跃站点的哈希表(hash table),并且将 addition \text{addition} addition操作规约称简单的两个同样尺寸的矩阵加法。这样增大残差连接的规模可以减少信息的损失。
-
DenseNets \text{DenseNets} DenseNets:实现的瓶颈问题与 ResNets \text{ResNets} ResNets类似。
-
4 4 4 实现 Implementation \text{Implementation} Implementation
-
为了高效实现 S C \rm SC SC与 V S C \rm VSC VSC,我们将输入张量与隐层状态分为两部分存储:
-
矩阵:矩阵维度为 a × m a\times m a×m,其中 a a a表示有 a a a个活跃站点,每行用于存储一个活跃站点;
-
哈希表:这个来源于GitHub@sparsehash,是一种用于存储稀疏数据的哈希表;
哈希表存储所有活跃站点的 ( l o c a t i o n , r o w ) (\rm location,row) (location,row)的二元组,其中 l o c a t i o n \rm location location是一个整数坐标的元组, r o w \rm row row则表示该活跃站点在特征矩阵(feature matrix)中的对应行。
- 笔者注:特征矩阵应该就是第一个矩阵, r o w \rm row row本质是一个索引键或编号, l o c a t i o n \rm location location才是活跃站点在原张量中的重要的位置信息。
-
-
定义 4.1 4.1 4.1:给定过滤器尺寸为 f f f的卷积核,定义规则书(rule book)是集合 R = ( R i : i ∈ { 0 , 1 , . . . , f − 1 } d ) R=(R_i:i\in\{0,1,...,f-1\}^d) R=(Ri:i∈{0,1,...,f−1}d),即一个由 f d f^d fd个整数矩阵(维度为 k i × 2 k_i\times2 ki×2)构成的集合。
- 笔者注: k i k_i ki的含义见本节末尾的小结第 3 3 3点。
-
SC ( m , n , f , s ) \text{SC}(m,n,f,s) SC(m,n,f,s)卷积层实现逻辑:
-
遍历输入张量的哈希表,我们通过遍历输出层的点来即时(on-the-fly)构建输出哈希表与规则书。当一个输出站点第一次被访问,就在输出哈希表中新建一个条目。
基于输入点与输出点在空间上的对应性(offset),在规则书中添加一条 ( input index,output index ) (\text{input index,output index}) (input index,output index)的记录,显然这将一共添加 k i k_i ki条记录。
-
初始化输出矩阵为零矩阵, ∀ i ∈ f \forall i\in f ∀i∈f,存在一个参数矩阵 W i ∈ R m × n W^i\in\R^{m\times n} Wi∈Rm×n, ∀ j ∈ { 1 , 2 , . . . , k i } \forall j\in\{1,2,...,k_i\} ∀j∈{1,2,...,ki},我们将输入特征矩阵的第 R i ( j , 1 ) R^i(j,1) Ri(j,1)行乘以 W i W^i Wi,然后与输出特征矩阵的第 R i ( j , 2 ) R^i(j,2) Ri(j,2)行相加,这种矩阵的加乘运算在 G P U \rm GPU GPU上是非常迅速的。
-
-
为了实现 VSC \text{VSC} VSC卷积层,我们对输出重用输入哈希表,并构造正确的规则书,注意因为稀疏模式没有发生改变,规则书依然可以继续重用(在 V G G , R e s N e t s , D e n s e N e t s \rm VGG,ResNets,DenseNets VGG,ResNets,DenseNets中),直到碰到一个池化层或下采样层(subsampling)。
若输入张量中有 a a a个活跃点(active points),则构建输入哈希表的成本为 O ( a ) O(a) O(a)
在 V G G , R e s N e t s , D e n s e N e t s \rm VGG,ResNets,DenseNets VGG,ResNets,DenseNets中,假设活跃站点的数量在每次池化运算中都减少乘数因子(multiplicative factor)倍,则构建所有哈希表和规则书的成本都是 O ( a ) O(a) O(a),这与网络的深度是无关的。
-
笔者注:这里的问题比较多,做一个小结。
-
活跃点就是活跃站点,这是小问题。
-
矩阵 R i R^i Ri一定是指矩阵 R i R_i Ri,这里原文的标记肯定是有误的。
-
SC ( m , n , f , s ) \text{SC}(m,n,f,s) SC(m,n,f,s)卷积层实现逻辑中第 2 2 2点非常 t r i c k y \rm tricky tricky,首先还是标记的问题, ∀ i ∈ f \forall i\in f ∀i∈f应该是 ∀ i ∈ { 0 , 1 , . . . , f − 1 } d \forall i\in\{0,1,...,f-1\}^d ∀i∈{0,1,...,f−1}d的意思,一共有 f d f^d fd个 d d d维向量的取值。
注意 d d d是输入数据的维数( R G B \rm RGB RGB图像即 d = 3 d=3 d=3,二维点阵图即 d = 2 d=2 d=2),注意本文中大概率是需要要求 i n c h a n n e l s = o u t c h a n n e l s \rm inchannels=outchannels inchannels=outchannels的,所以 d d d就是卷积核中过滤器的数量,这就意味着 i i i和卷积核中每个过滤器中每个元素对应(或者也可以理解为跟过滤器上每个元素相对应,如果认为一个卷积核只有一个过滤器的话,当然是广义上的过滤器),所以 i i i本质是一个位置索引。
所以规则书上记录了输入与输出在过滤器下映射的一个对应关系(当然是一对一,因为只考虑了输出对应的输入中心点)。那么 k i k_i ki应该就是通过移动过滤器窗口在整个图像上移动的次数。
而过滤器每移动一次都会产生一个权重矩阵 W i W^i Wi(其实 W i W^i Wi难道不应该都是一样的吗? C N N \rm CNN CNN参数共享啊!),这样看起来一切都说得通了。
总之原文第 4 4 4节含糊其辞,很多标记都没有好好说明,非常痛苦,而且本文的项目代码是需要在 L i n u x \rm Linux Linux上安装的,笔者还没有时间去查源码中的逻辑。
-
下采样可以参考博客图像的上采样(upsampling)与下采样(subsampled),这应该是图像处理的一个概念,笔者似乎没有了解过,可能类似池化。
-
哈希表算是数据结构的概念了,这里不多说明,理解为字典即可。
-
5 5 5 实验 Experiments \text{Experiments} Experiments
-
CASIA \textbf{CASIA} CASIA数据集:下载地址
其中包含 3766 3766 3766个 GBK level-1 \text{GBK level-1} GBK level-1的汉字,每个汉字大约有 240 240 240个训练图像和 60 60 60个测试图像。
C J V K \rm CJVK CJVK汉字是本文模型最好的测试案例,因为它们是在 64 × 64 64\times 64 64×64点阵上书写,大约只有 8 % 8\% 8%的像素点是活跃的(即稠密),这个百分比将会在池化后大规模下降,因为笔迹是非常稀疏的。
-
ModelNet-40 \textbf{ModelNet-40} ModelNet-40数据集:下载地址
其中包含 2468 2468 2468个 C A D \rm CAD CAD模型,对应 40 40 40个不同类别,参考文献 [ 8 ] [8] [8]中有该数据集的预处理方法。
5.1 5.1 5.1 CASIA \text{CASIA} CASIA实验结果 Results on CASIA \text{Results on CASIA} Results on CASIA
-
实验细节:
- e p o c h = 100 \rm epoch=100 epoch=100
- batchsize = 100 \text{batchsize}=100 batchsize=100
- 优化器为随机梯度下降(stochastic gradient decreasing,下简称为 S G D \rm SGD SGD),动量因子为 0.9 0.9 0.9
- 权重衰减(weight decay)为 1 0 − 4 10^{-4} 10−4
- 学习率(learning rate)每个 e p o c h \rm epoch epoch衰减 5 % 5\% 5%
- 未采用数据增强
-
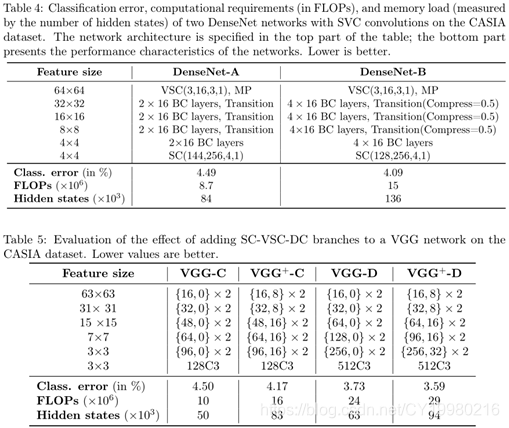
Table 2, Table 3, Table 4 \text{Table 2, Table 3, Table 4} Table 2, Table 3, Table 4中分别是 V G G , R e s N e t s , D e n s e N e t s \rm VGG,ResNets,DenseNets VGG,ResNets,DenseNets的实验评估情况;自己看吧,其实基本结论就是 F L O P s \rm FLOPs FLOPs减少大约 50 % 50\% 50%,稀疏模型误差基本持平原模型的情况。

-
Figure 3 \text{Figure 3} Figure 3中有一个针对 CASIA \textbf{CASIA} CASIA数据集实验的总体情况的图像,似乎也没什么用。
5.2 5.2 5.2 ModelNet \text{ModelNet} ModelNet实验结果 Results on ModelNet \text{Results on ModelNet} Results on ModelNet
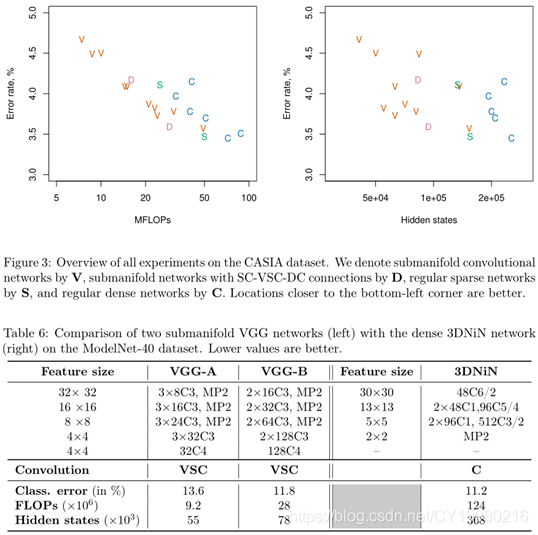
- 详见 Table 6 \text{Table 6} Table 6,本小结原文写得很简约,估计是没有做多少工作。
6 6 6 相关工作 Related Work \text{Related Work} Related Work
- 在引入部分已经提到了三篇相关研究(参考文献
[
1
,
2
,
9
]
[1,2,9]
[1,2,9]),本节主要谈论了参考文献
[
9
]
[9]
[9]的
O
c
t
N
e
t
s
\rm OctNets
OctNets:
- 本文提出的 S C N \rm SCN SCN要远比 O c t N e t s \rm OctNets OctNets稀疏,具体而言后者使用 oct-trees \text{oct-trees} oct-trees来存储数据,递归地将一个立方网格切分未 2 3 2^3 23块子立方,直到子立方为空或包含单一的活跃站点为止。
- 本文对比了 S C N \rm SCN SCN与 O c t N e t s \rm OctNets OctNets的性能,用的是 ModelNet-40 \textbf{ModelNet-40} ModelNet-40数据集,因为这是一个 3 D 3\rm D 3D图形数据集,是后者比较适用的,结果表明 O c t N e t s \rm OctNets OctNets的计算成本是 V S C \rm VSC VSC卷积层的 60 60 60倍。同时在内存占用上, S C N \rm SCN SCN同样表现出巨大优势。
- 本文认为可以将参考文献 [ 9 ] [9] [9]的一些内容结合进来,如使用 oct-trees \text{oct-trees} oct-trees作为 V S C \rm VSC VSC卷积层的一种具体的哈希函数,这可能可以进一步提升 V S C \rm VSC VSC的性能。
7 7 7 结论 Conclusion \text{Conclusion} Conclusion
无重要内容,本文提供的项目代码理论上可以复现本文所有的实验结果。
参考文献 References \text{References} References
[1]M. Engelcke, D. Rao, D. Z. Wang, C. H. Tong, and I. Posner. Vote3deep: Fastobject detection in 3d point clouds using efficient convolutional neural networks. 2016.
[2]B. Graham. Sparse3D convolutional neural networks. In BMVC 2015.
[3]K. He, X. Zhang, S. Ren, and J. Sun. Identity mappings in deep residual networks. ECCV, 2016.
[4]G. Huang, Z. Liu, K. Q. Weinberger, and L. van der Maaten. Densely connected convolutional networks. 2016.
[5]Y. LeCun, J. Denker, and S. Solla. Optimal brain damage. In NIPS, 1990.
[6]B. Liu, M. Wang, H. Foroosh, M. Tappen, , and M. Penksy. Sparse convolutional neural networks. In CVPR, 2015.
[7]C. L. Liu, F. Yin, D. H. Wang, and Q. F. Wang. CASIA online and offline chinese handwriting databases. In ICDAR, pages37–41. IEEE Computer Society, 2011.
[8]C. R. Qi, H. Su, M. Niessner, A. Dai, M. Yan, and L. J. Guibas. Volumetric and multi-view CNNs for object classification on 3D data, Apr. 29 2016.
[9]G. Riegler, A. O. Ulusoy, and A. Geiger. Octnet:Learning deep 3D representations at high resolutions. CoRR, abs/1611. 05009, 2016.
[10]K. Simonyan and A. Zisserman. Very deep convolutional networks for large-scale image recognition. 2014.
[11]C. Szegedy, W. Liu, Y. Jia, P. Sermanet, S. E. Reed, D. Anguelov, D. Erhan, V. Vanhoucke, and A. Rabinovich. Going deeper with convolutions. CoRR, abs/1409. 4842, 2014.
[12]S. Xie, R. Girshick, P. Dollár, Z. Tu, and K. He. Aggregated residualtransform ationsfor deep neural networks. arXiv preprint arXiv:1611. 05431, 2016.
[13]M. D. Zeiler, D. Krishnan, G. W. Taylor, and R. Fergus. Deconvolutionalnetworks. In CVPR, 2010.
图表汇总































 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








