Codeforces Round #696 (Div. 2) C. Array Destruction（模拟+思维）

 

 

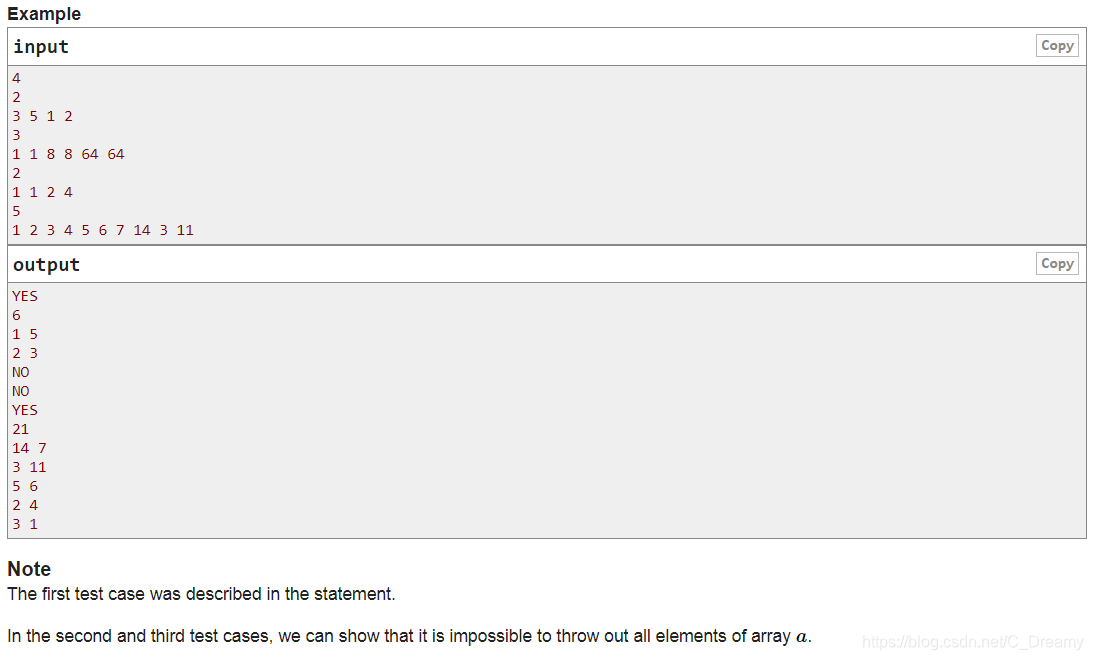
有 2n 个数，第一次任意选择两个数，将他们删掉，记这两个数的最大值为 res，再从剩下的 2n-2 个数中选择两个数，在将他们删掉，但是这两个数要满足相加等于 res，将 res 更新为这两个数的最大值，以此类推，直至将所有数删掉，问是否可以完成，如果完成输出步骤 

题目中 n=1e3 ，摆明了要来暴力，题目中 a[i]<=1e6，可以开数组大小至 1e6，数组量再大一点可能要离散化，这里采用 map

推两遍样例可以发现，如果存在答案的话，那么有种博弈的感觉，第一次一定将最大的数字去掉，剩下的每一次选择两个数，其中必有一个最大数，最后的答案其实就是在第一次取的时候将一个孤立数去掉，这样剩下的数可以满足条件

要注意的是，将两个数消去时，可能存在这两个数相等的情况，这里要特判一下

const int N=2e5+5;

    int n,m;
    int i,j,k;
    int a[N];
    map<int,int> mp,vis;

int main()
{
    rush(){
        cin>>n;
        mp.clear();
        for(int i=1;i<=n*2;i++) sd(a[i]),mp[a[i]]++;
        sort(a+1,a+1+2*n);
        int res=a[2*n],flag=0,tmp=0;
        vector<pii> ans;
        for(int i=2*n-1;i;i--){
            ans.clear(),vis=mp;
            res=a[2*n];
            ans.pb(mp(res,a[i]));
            vis[res]--,vis[a[i]]--;
            flag=1;
            for(int j=2*n-1;j && flag;j--){
                if(vis[a[j]]==0) continue;
                if(res-a[j]!=a[j] && vis[res-a[j]] && vis[a[j]]) vis[res-a[j]]--,vis[a[j]]--,ans.pb(mp(res-a[j],a[j])),res=max(res-a[j],a[j]);
                else if(res==a[j]*2 && vis[a[j]]>=2) vis[a[j]]-=2,ans.pb(mp(a[j],a[j])),res=a[j];
                else flag=0;
            }
            if(flag) break;
        }
        if(flag==0) puts("NO");
        else{
            puts("YES");
            cout<<ans[i].fr+ans[i].sc<<endl;
            for(int i=0;i<ans.size();i++){
                cout<<ans[i].fr<<" "<<ans[i].sc<<endl;
            }
        }
    }
    PAUSE;
    return 0;
}