首遇lancer
★☆ 输入文件:lancer.in 输出文件:lancer.out 简单对比
时间限制:1 s 内存限制:256 MB
【题目背景】
第五次圣杯之战。kito乱入。
【题目描述】
一个宁静的夜晚,kito在学校的楼顶乘凉。
“多么美好的星空啊,可惜只有在学校才能看到。”kito发表感慨。
天上闪过一道星光,划过天际,kito正以为看到了少有的流星,谁知一声巨响降落在楼顶。
“哟,年轻人。”烟雾散去,是lancer。
“lancer?天哪,你找我干什么,虽然我乱入了,但是我还没有servant。”kito立马认怂。
“没事,今天不是来打架的,”lancer帅气的一笑,kito不禁看呆。
“saber还没出现,还没到我的戏份,所以闲的无聊,”lancer说,“于是就去破解教主的密码箱,但是密码太恶心了,像我这种帅气的英灵自然是不会的啦。听说你最近刚复习完数论,我来请教一下一个正整数的因数个数”。
“枚举一下不就好了。”
“但是它是求和啊,要求n的所有因数的的因数个数之和。”
“……”
“由于教主讨厌大于等于109+7的数,所以你只需要把答案对109+7取模后的值告诉我。如果你答对了,我就和你一起分享密码箱里的宝物,同时陪你一天哦~。”
一听lancer会陪他一天,kito非常的激动,但是kito实在是太弱了,所以他只能拜托你,为了kito的幸福生活,希望你能把答案告诉他。
【输入格式】
输入一共一行,有一个整数,为n。
【输出格式】
共一行,为∑i=1N [Nmod i==0]F[i]对109+7取模的值,F[i]表示i的因数个数。
【输入样例1】
1
【输出样例1】
1
【输入样例2】
10
【输出样例2】
9
【数据范围】
30%的数据满足n<=5000
70%的数据满足n<=100000
90%的数据满足n<=10000000
100%的数据满足n<=1000000000
【来源】
Hzoi 2016
题目分析:
根据唯一分解定理,可以将N分成有限个素数的乘积,即
然后不难发现任意几个a+1相乘就是对应p的a次方的乘积的因数个数,并且对应p的a次方的乘积是N的因数,这样,枚举所有情况相加即可得到ans,但简单枚举会超时。但数学方法可以推出一个不错的计算方法: 设f(a1,a2,a3...an)表示ans,容易得到f(a1,a2,a3...an-1)*((an+1+1)*(an+1)/2)=ans;然后不断向前推导答案即为((a1+1+1)*(a1+1)/2)*((a2+1+1)*(a2+1)/2)*...*((an+1+1)*(an+1)/2)。
代码:
#include<iostream>
#include<cstdio>
using namespace std;
const int MAXN=1000;
bool vis[MAXN];
int p[MAXN];
int a[MAXN];
int c=0;
int n;
int ans=1;
int main()
{
freopen("lancer.in","r",stdin);
freopen("lancer.out","w",stdout);
scanf("%d",&n);
for(int i=2;i<=n;i++)
if(n%i==0)
{
while(n%i==0)
{
n/=i;
a[c]++;
}
c++;
} //唯一分解定理,生成a序列
for(int i=0;i<c;i++)
a[i]++,ans=ans*((1+a[i])*a[i])/2; //得到答案,分析数据范围不用取模
printf("%d",ans);
return 0;
}






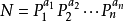














 1002
1002

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








