【wolfram数模-小波-上】

一、介绍

傅里叶变换分解一个信号，转化为该信号的正弦和余弦分量，并将时间序列从时域转换为频域，“将信号以频率（frequencies）形式呈现”。

傅里叶变换是对信号进行处理加工，原本只包含时域信息而不包含频率信息，通过傅里叶变换能够得到频率信息。

• 频率的单位是赫兹，表示每秒循环次数
• 变换快，频率高
• 变换慢，频率低

类别	公式	解释
傅里叶变换公式（连续）	$$F(\omega )={\int }_{-\infty }^{\infty }f(t)e^{-j\omega t}dt$$	$$\omega$$表示频率
傅里叶逆变换公式（连续）	$$f(t)=\frac{1}{2\pi }{\int }_{-\infty }^{\infty }F(\omega )e^{j\omega t}d\omega$$	$$t$$表示时间
离散傅里叶变换（DFT）	$$X[k]=\sum _{n=0}^{N-1}f[n]e^{-j\frac{2\pi }{N}kn}$$
逆离散傅里叶变换（IDFT）	$$f[n]=\frac{1}{N}\sum _{k=0}^{N-1}X[k]e^{j\frac{2\pi }{N}kn}$$

所以：积分符号 ∫ 、求和符号 ∑ 对应着：连续、离散，本质都是一个意思，都是做加法。

看一个应用实例

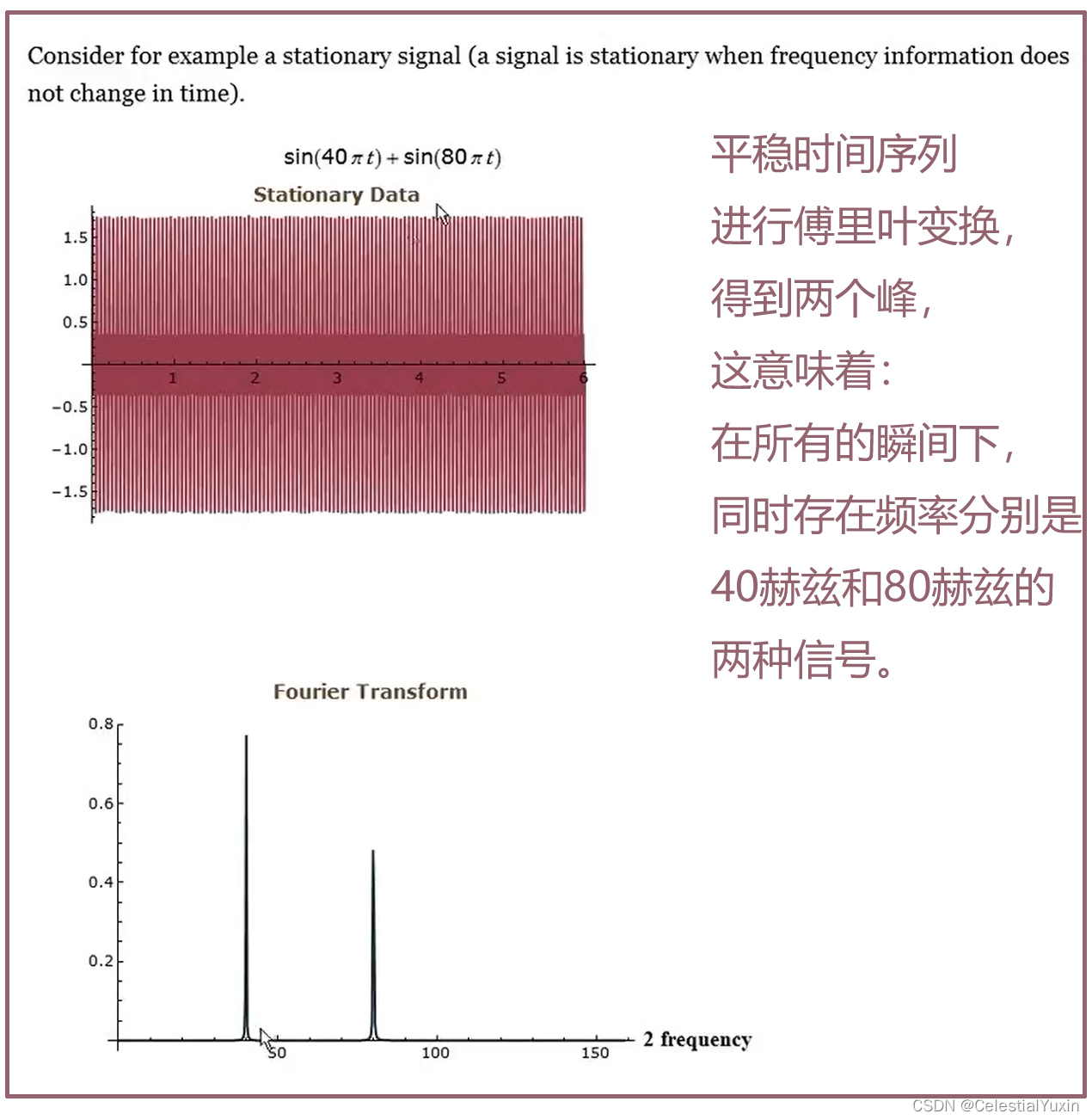
再看一个应用实例
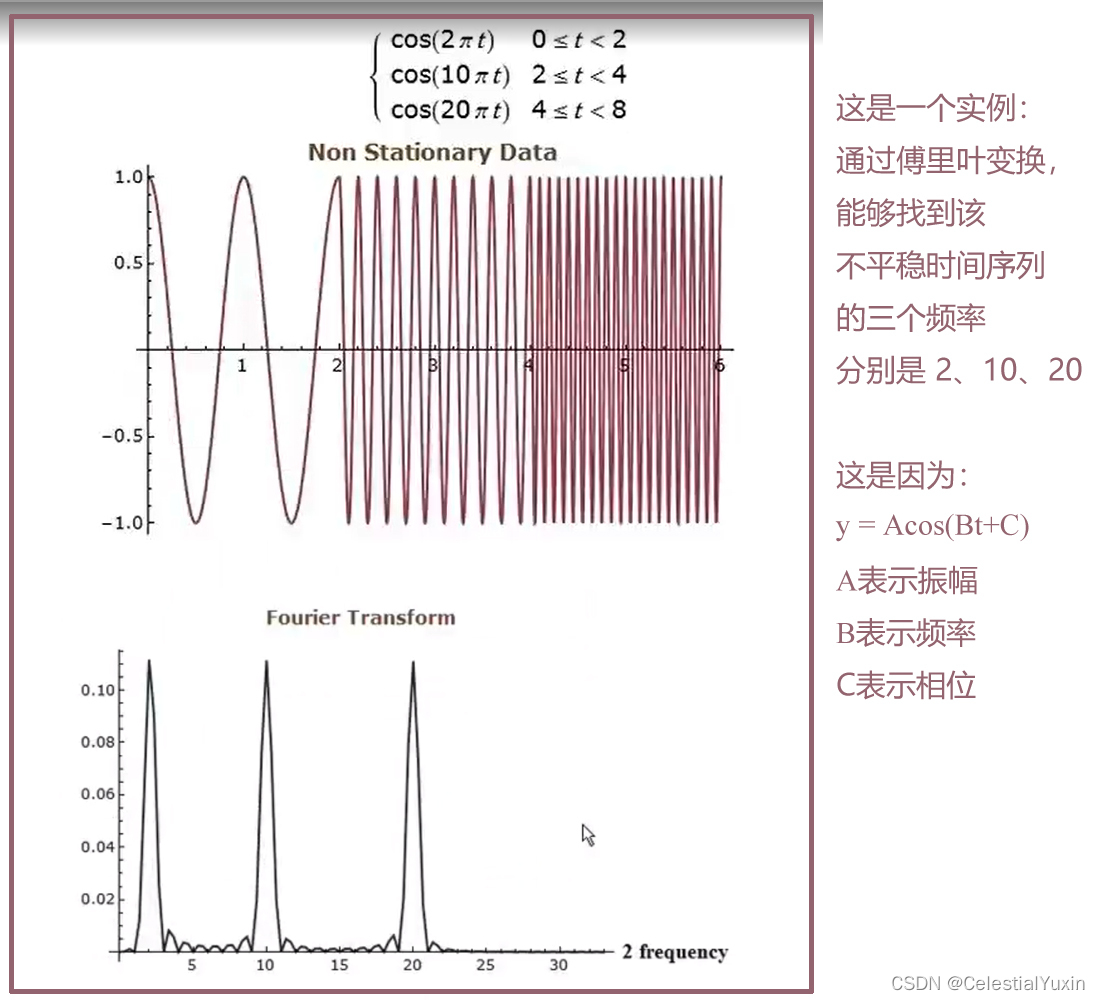但是这个实例没能提供完整的信息，比如，“该时间序列从什么时候改变了频率”等。为了克服这些问题，人们开始利用窗口傅里叶变换(Windowed Fourier transform)和短时傅里叶变换(short-time Fourier transform)

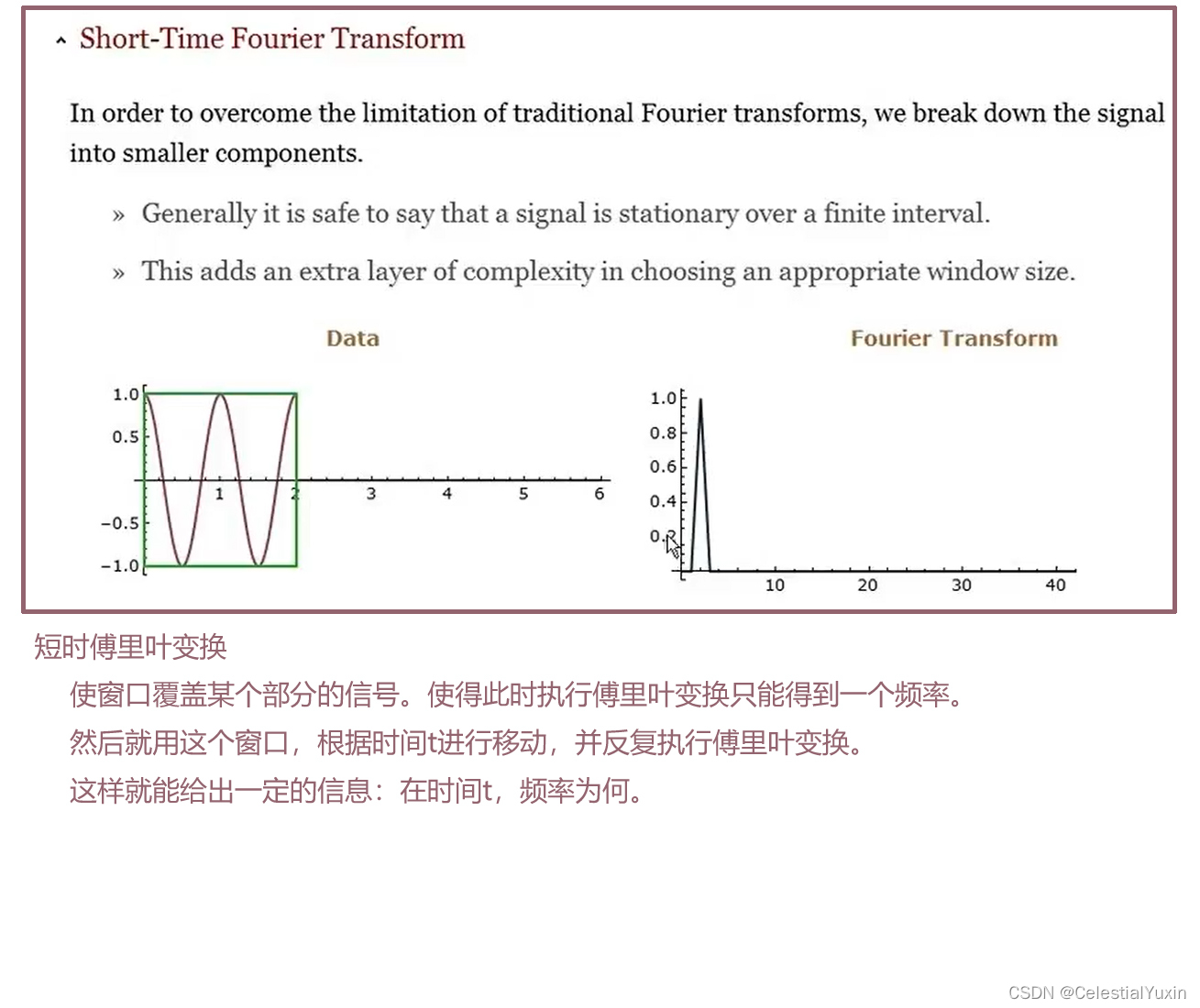
短时傅里叶变换面临的问题是：需要选择窗口的大小，需要解释为什么选择这样尺寸的窗口等等。
而这，就给我们带来的了一个概念：小波分析。

- ① 具体实例：

如果我们的信号是一个非常良好（良好应该是说振幅频率都是平稳的）的正弦和一个超短时（1/511秒，只有把横轴也设置为500多个时刻才能看得见）的指数函数组合而成。执行傅里叶变换，会怎么样呢？

傅里叶变换只识别出来一个峰（峰在横轴上的位置代表该正弦函数的频率，4赫兹），会完全丢失那个突然出现快速消失的信号。
在地震和心电图等实际应用当中，这种突然出现并且快速消失的信号（e.g.心跳不规则）可能是至关重要的，不应该丢失。
那如果是小波变换处理相同的信号呢？？

所执行的是连续小波变换–paul wavelet
得到一个牛油果绿色图，就是的“小波尺度图”
[7,1]随着octave增大，只能观察到sin函数
[2,1]随着octave减小，能观察到在横轴0.3附近发生了某个事件，并且持续一定的时间。

小波分析本质上是使用小波函数对一个信号进行分解，最终你得到一系列系数。
psi ψ 小波函数 --> Detail coefficients
phi Φ 缩放函数 --> Coarse coefficients
下图中的树形结构就是多分辨率分析。

看一个实例——连续小波变换

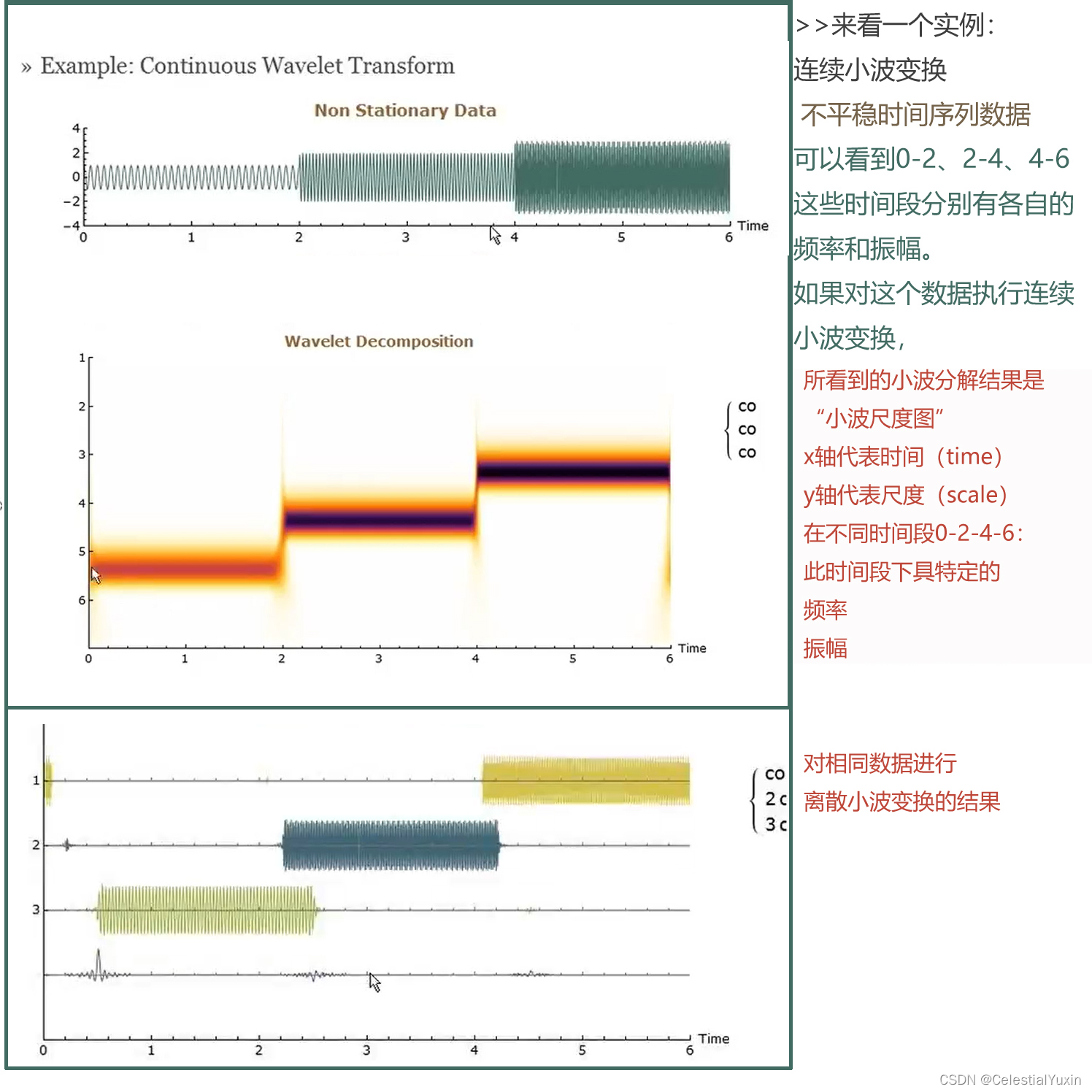
一些时&频解决方案：
在进行任何类型的时间序列分析时，我们应该问的一些基本问题是，你想在信号中寻找什么样的特征，以及分析的目的是什么？如果您只对信号中的频率成分感兴趣，那么傅立叶变换在大多数情况下都能胜任。相反，如果你感兴趣的是信号中存在的特定特征，以及信号的振幅和持续时间，那么像小波变换这样的方法将是你的不二之选。

1. 对时序进行频率侦测

单一频率(平稳时间序列)

信号是：某种频率的余弦函数
所执行的是：
6阶Gabor Wavelet
octave = 8
voice = 4



能够通过移动进度条探查导信号中的高频或低频成分

两个频率

信号是：两个不同频率的余弦函数
所执行的是：
6阶Gabor Wavelet
octave = 8
voice = 4



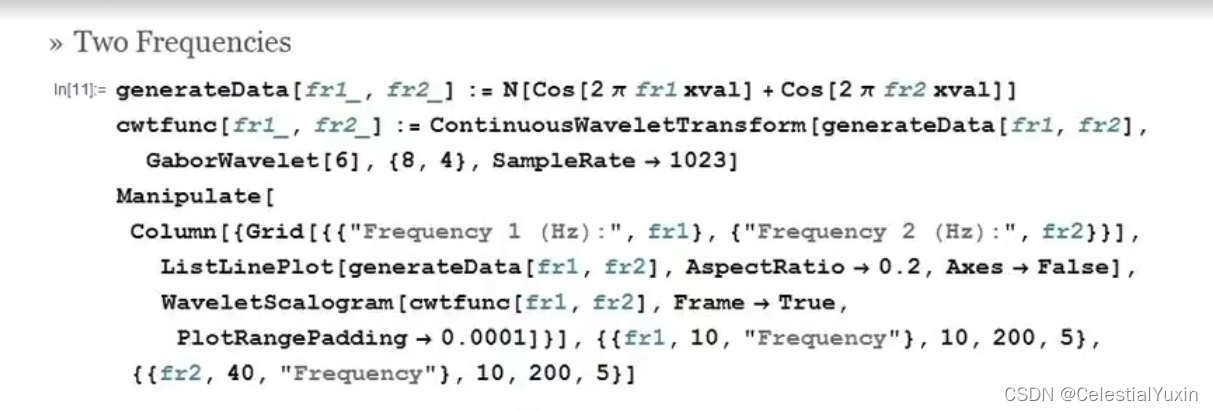
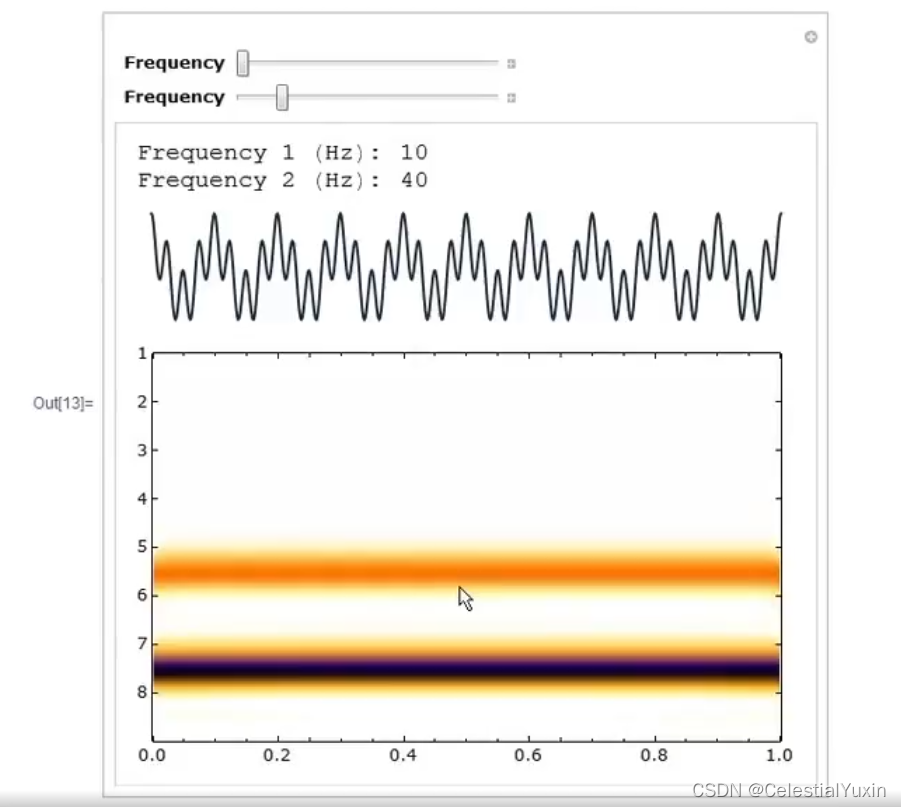
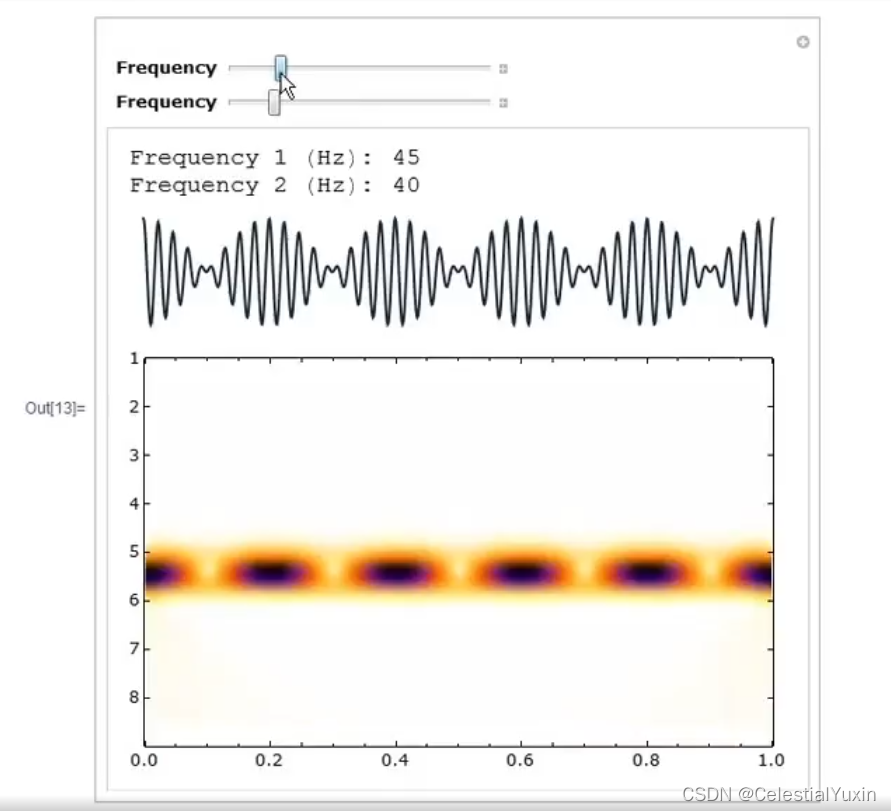
取决于这两者频率如何结合，两个黄色色带也能合并成一条——调幅（AM)。