#leetcode#Permutation Sequence

The set [1,2,3,…,n] contains a total of n! unique permutations.

By listing and labeling all of the permutations in order,
We get the following sequence (ie, for n = 3):

1. "123"
2. "132"
3. "213"
4. "231"
5. "312"
6. "321"

Given n and k, return the kth permutation sequence.

Note: Given n will be between 1 and 9 inclusive.

这题是纯数学题。。。本来用Permutations的递归写法写了一遍， TLE， 说是数学题也可以， 说是考察算法也可以， 其实还是观察规律，或者说考察对如何生成permutation的理解。

找规律：http://bangbingsyb.blogspot.com/2014/11/leetcode-permutation-sequence.html

构造permutation理解：http://yucoding.blogspot.com/2013/04/leetcode-question-68-permutation.html

这里推荐从如何构造permutation来理解如何得到第K个permutation，摘录Yu神的一些讲解在这：

Analysis:

One way to solve the problem (can only pass the small test) is to generate from the 1st permutation to the required one (similar to the problem  Next permutation .). However, when n=9, the last permutation is the 362880th one, which is too time consuming.

A better way is to fully use the properties of permutation: the total number of permutation with length n is n!.
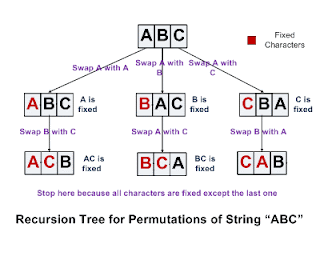
First, let's take a look at how permutation works:

Major steps are swap and fix:

Here in order to grow the tree,  every time start the first unfixed element in each node, generate child nodes by swapping the first element with every other element.The leave nodes are those do not have element to swap. 

So, when we have the idea of how to generate the permutation, next step is to generate it faster. Think the tree in this way:

                         ABC

         /                   |                    \

      ABC              BAC               CBA

    /       \             /      \               /    \

ABC  ACB     BAC BCA    CBA CAB

Every leave node is a permutation. Take a look at the second level, each subtree (second level nodes as the root), there are (n-1)! permutations in it.  Totally there are n nodes in 2nd level, thus the total number of permutations are n*(n-1)!=n!.

So, what we want to do is to locate one permutation among the leave nodes. The simple method is to generate and search each leave node until we find the one. Now, what we can do here we want to skip some trees to reduce the complexity. e.g. in the above tree, if we know the required leave node is in the third sub tree (under CBA), we can skip the first two and search from the "CBA".

Say we have the required permutation is the kth one, first we can locate which subtree it belongs to in the 2nd level, by computing s = k / ((n-1)!). Then we get the sth subtree, and set k=k%((n-1)!) , now search the sub tree until we get the leave node. How to get the sth subtree root node? Just like the idea of how permutation works (the first figure): Just put the sth elment after fixed letter.  e.g. ABCD,  we want the 3rd subtree root node in 2nd level, just put C in the 1st place, which is CABD;   For ABCDE, we want the 3rd subtree root node in the 3rd level, it is ADBCE.

public class Solution {
    public String getPermutation(int n, int k) {
        if(n <= 0 || k <= 0)
            return "";
        int factorial = 1;
        // get (n - 1)!
        for(int i = 2; i < n; i++){
            factorial *= i;
        }
        StringBuilder sb = new StringBuilder();
        List<Integer> nums = new ArrayList<Integer>();
        for(int i = 0; i < n; i++){
            nums.add(i + 1);
        }
        // k-- because index is zero based.
        k--;
        while(n > 0){
            int index = k / factorial; // here factorial = (n - 1)! for the first while loop
            k %= factorial;
            sb.append(nums.get(index));
            nums.remove(index);
            if(n > 1)
                factorial /= (n - 1);
            n--;
        }
        return sb.toString();
    }
}

Leetcode discuss中看到一个很neat的用linkedlist的写法：

public String getPermutation(int n, int k) {
    LinkedList<Integer> list = new LinkedList<>();
    for (int i = 1; i <= n; i++) list.add(i);
    int fact = 1;
    for (int i = 2; i <= n; i++) fact *= i; // factorial

    StringBuilder strBuilder = new StringBuilder();
    for (k--; n > 0; n--) {
        fact /= n;
        strBuilder.append(list.remove(k / fact));
        k %= fact;
    }

    return strBuilder.toString();
}