题目链接:https://leetcode.com/problems/generate-parentheses/
题目:
Given n pairs of parentheses, write a function to generate all combinations of well-formed parentheses.
For example, given n = 3, a solution set is:
"((()))", "(()())", "(())()", "()(())", "()()()"解题思路:
这其实是一个不断选择左括号和右括号的问题,即需要递归求解
- 递归的前提是给定当前剩余的左右括号数。
- 递归条件:
- 当右括号剩余数小于左括号剩余数时,括号组合出现差错,不做其余操作直接返回。
- 当左右括号剩余数量都为 0 时,括号组合完成,将该字符串放入 list 中。
- 当左括号剩余数大于 0 时,将左括号放在当前括号字符串的末尾,进入下一轮递归。
- 当右括号剩余数大于左括号剩余数时,将右括号放在当前括号字符串的末尾,进入下一轮递归。
public class Solution {
public List<String> generateParenthesis(int n) {
List<String> list = new ArrayList();
if(n <= 0)
return list;
else
helper(n, n, "", list);
return list;
}
public void helper(int l, int r, String item, List<String> res) {
if(r < l)
return;
if(l == 0 && r == 0) {
res.add(item);
return;
}
if(l > 0)
helper(l - 1, r, item + "(", res);
if(r > l)
helper(l, r - 1, item + ")", res);
}
}8 / 8 test cases passed.
Status: Accepted
Runtime: 220 ms补充:
参考链接:http://blog.csdn.net/linhuanmars/article/details/19873463
这道题其实是关于卡特兰数的,如果只是要输出结果有多少组,那么直接用卡特兰数的公式就可以。关于卡特兰数,请参见卡特兰数-维基百科,里面有些常见的例子,这个概念还是比较重要的,因为很多问题的原型其实都是卡特兰数,大家可以看看。特别是其中
这个递推式的定义,很多这类问题都可以归结成这个表达式。这个题对于C的定义就是第一对括号中包含有几组括号。因为第一组括号中包含的括号对数量都不同,所以不会重复,接下来就是一个递归定义,里面又可以继续用更小的C去求组合可能性。








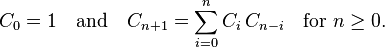














 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








