强连通分量

强连通分量

前置芝士

首先熬过了 树剖，$mjl$ 终于开始讲解一些码量偏小的题目。

于是，就愉快地探索什么是强连通分量……

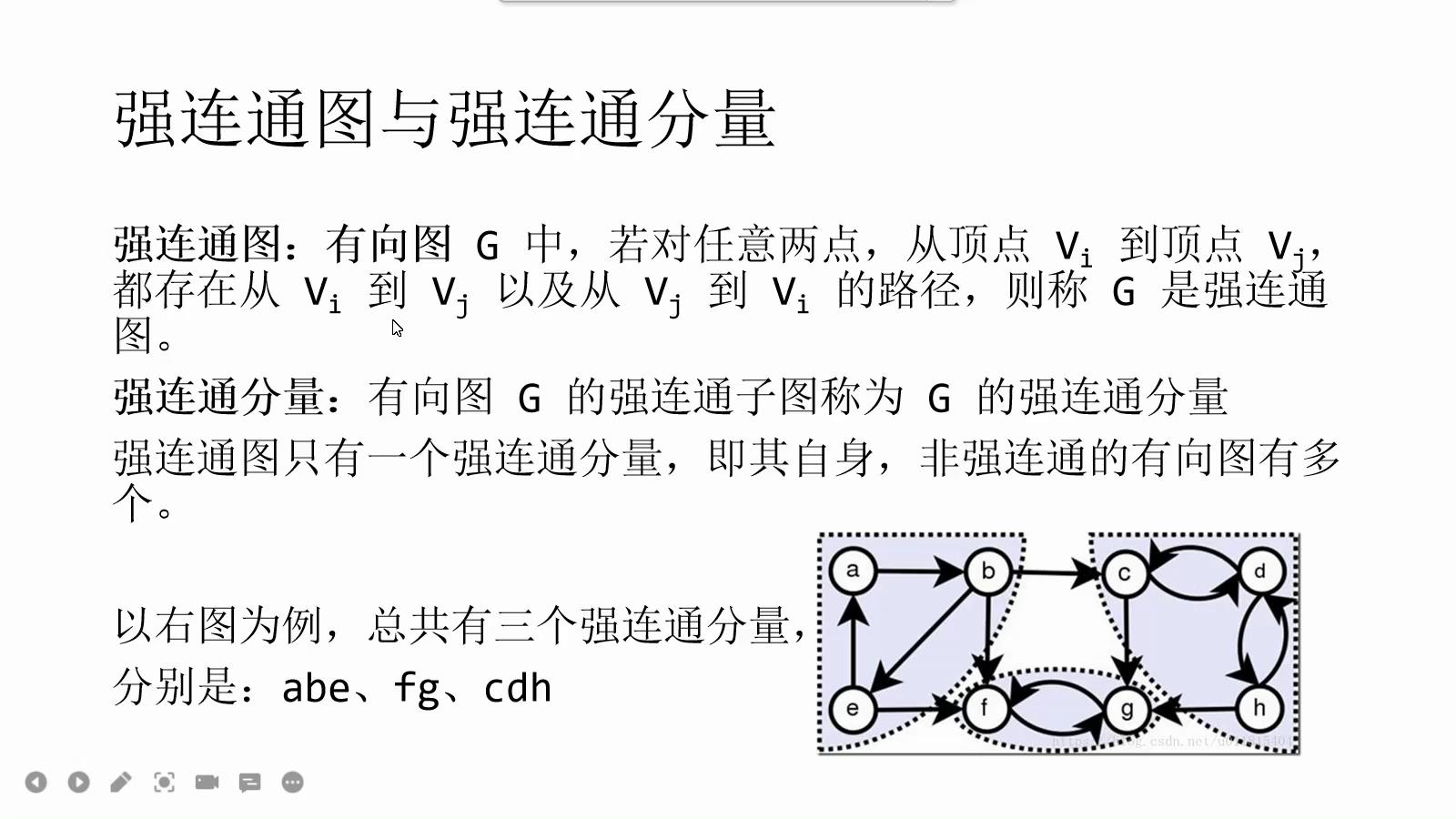
以上是它的一些基本概念。

其实强连通就是一个环，主要是解决一些有向图求最值问题（最少需要几个物品完成所有节点覆盖……）。

Tarjan

之前在学习 LCA 时就以接触过这位大佬的算法，是离线的，时间复杂度达到了优秀的 $O(n+q)$，不过常数极大，被树剖秒掉。但是 Tarjan 在 强连通分量 是在线的，也是正常搜索的时间复杂度，于是它就成为了不二之选。

---

$Robert$ $E.$ $Tarjan$（罗伯特·塔扬，$1948$~），生于美国加州波莫纳，计算机科学家。

$Tarjan$ 发明了很多算法和数据结构。不少他发明的算法都以他的名字命名，以至于有时会让人混淆几种不同的算法。比如求 各种连通分量的Tarjan 算法，求 LCA（Lowest Common Ancestor，最近公共祖先）的 Tarjan 算法。并查集、Splay、Toptree 也是 $Tarjan$ 发明的。

---

首先送上最诚挚的膜拜。

然后开始对 Tarjan 的讲解。

首先需要用到一个东西叫做追溯值（上图有），并且需要用到一个栈来存储当前已经遍历到的结点（后面有用）。追溯值用来判定是否是强连通分量，其中的 $low$ 数组调整分为以下两种情况：（不妨假设当前遍历到的结点为 $u$，即将遍历到的结点为 $v$）

1.如果 $v$ 未被遍历到（即 $df{n}_v=0$，此处 $dfn$ 数组存储的是树的 dfn序），那么取：

$lo{w}_u=\min (lo{w}_u,lo{w}_v)$.

2.如果不满足条件1但是并没有被记录属于任何一个强连通分量（即 $pe{r}_v=0$，此处 $per$ 数组表示该结点属于强连通分量的标号，未被标记即为初始值 $0$），那么取：

$lo{w}_u=\min (lo{w}_u,Df{n}_v)$.

有了这样的处理，接下来进行强连通分量的标记环节。

---

如果进过了以上的处理后 $lo{w}_u=Df{n}_u$，那么就可以确定 $u$ 所在的强连通分量的所有结点都已被遍历到（即都已放入了栈），于是我们再开一个 $per$ 数组，它的含义上文已解释，一个整数型变量 $ret$ 用于存储当前的编号。

于是首先：

per[u]=++cnt;

然后：

while(1){
	int tmp=s.top();s.pop();
	per[tmp]=cnt;
	if(tmp==x)break;
}

其中 $s$ 为之前处理出来的栈，知道栈弹出的元素等于当前遍历到的元素，那么整个强连通分量就已遍历结束。

Floyd

上一次接触 Floyd，是在求全源最短路时，它的代码框架如下：

int dis[505][505];
//code.
for(int k=1;k<=n;++k){
    for(int x=1;x<=n;++x){
        for(int y=1;y<=n;++y){
            dis[x][y]=min(dis[x][y],dis[x][k]+dis[k][y]);
		}
	}
}

很显然，它的时间复杂度为 $O(n^3)$，虽说很大，不过图论的题目一般 $n$ 都比较小，所以是完全可过的。

而现在关于它的运用就是判断是否可以相通，如下：

bool dis[505][505];
//code.
for(int k=1;k<=n;++k){
    for(int x=1;x<=n;++x){
        for(int y=1;y<=n;++y){
            dis[x][y]|=dis[x][k]&&dis[k][y];
		}
	}
}

这只是强连通分量的一个基本运用。

出度与入度

首先必须在有向图中，对于一个结点，用多少条边直接到达了它，就为它的入度，反之则为出度。

它们的求取防止为下（首先要在跑过一次 Tarjan 的基础下，不妨设 $R$ 数组为入度，$C$ 数组为出度）：

#include<bits/stdc++.h>
using namespace std;
inline int read(){
	int ch=0,num=0;
	char c=getchar();
	while(!isdigit(c))ch|=(c=='-'),c=getchar();
	while(isdigit(c))num=(num<<1)+(num<<3)+(c^48),c=getchar();
	return ch?-num:num;
}
inline void write(int x){
	if(x<0)putchar('-'),x=-x;
	if(x>=10)write(x/10);
	putchar(x%10+'0');
}
int n,Dfn[3005],low[3005],ret,cnt,per[3005],val[3005],R[3005],C[3005];
vector<int>G[3005];
stack<int>s;
inline void dfs(int x){
	Dfn[x]=low[x]=++cnt,s.push(x);
	for(int i=0;i<G[x].size();++i){
		if(!Dfn[G[x][i]]){
			dfs(G[x][i]);
			low[x]=min(low[x],low[G[x][i]]);
		}else if(!per[G[x][i]]){
			low[x]=min(low[x],Dfn[G[x][i]]);
		}
	}
	if(low[x]==Dfn[x]){
		++ret;
		while(1){
			int tmp=s.top();s.pop();
			per[tmp]=ret;
			if(tmp==x)break;
		}
	}
	return;
}
signed main(){
	n=read();
	for(int i=1;i<=n;++i){
		int x=read(),y=read();
		G[x].push_back(y);
	}
	for(int i=1;i<=n;++i){
		if(!Dfn[i]){
			dfs(i);
		}
	}
	for(int i=1;i<=n;++i){
		for(int j=0;j<G[i].size();++j){
			if(per[i]!=per[G[i][j]]){
				++C[per[G[i][j]]];
                ++R[per[i]];
			}
		}
	}
	return 0;
}