初勘数据处理之滤波算法(一)

初勘数据处理之滤波算法(一)

在电气测量系统中对某一对象的状态或特征测量的过程中往往会出现一些硬件电路无法消除的误差，这时我们就需要祭出最后的神器——软件滤波；本文将针对实际测量中板材厚度数据进行滤波分析，寻找最合适的滤波算法；
目标：对板材进行一系列相关检测试验，得到观测时间序列根据处理要求，对其进行预处理，得到平稳，精准的数据。
(一). 一维高斯滤波
对动态线性测厚的测量原理及产生噪声的原因进行分析，可以将板材测厚划归线性高斯系统，对于合成板的测量厚度将呈现高斯分布，而测量误差，也就是测量噪声也会呈现期望为0的高斯分布，
1).算法背景：
了解高斯滤波之前，我们首先熟悉一下高斯噪声。高斯噪声是指它的概率密度函数服从高斯分布（即正态分布）的一类噪声。如果一个噪声，它的幅度分布服从高斯分布，而它的功率谱密度又是均匀分布的，则称它为高斯白噪声。
2).算法原理：
高斯滤波器是一类根据高斯函数的形状来选择权值的线性平滑滤波器。高斯平滑滤波器对于抑制服从正态分布的噪声非常有效。
正态分布的概率密度函数：

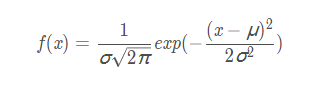
通过设定的期望u及标准差sigma，得到高斯滤波的高斯模板，通过模板对待处理点及周围数据点进行加权运算，得到最后的滤波结果；

%输入数据序列：dataList