提出一种基于低秩纹理先验的卡通纹理图像分解模型，利用全变差范数和全局核范数表征卡通和纹理分量。模型简单且能恢复清晰纹理。采用部分并行分裂法求解，实验显示其迭代次数和计算时间较短。
论文阅读:一个自定义的结构化卡通纹理图像分解低秩先验模型
目录
4.1. Clear image decomposition: 𝛷 =I
4.4. Image deblurring and inpainting: 𝛷 = 𝑺𝑩
0、摘要
纹理分量的数学表征在图像分解中起着重要作用。本文研究了一种基于低秩纹理先验的卡通纹理图像分解模型，该模型利用全变差范数和全局核范数分别对卡通分量和纹理分量进行表征。我们的分解模型不仅简单，而且在恢复比其他新模型更清晰的纹理(或细节)的意义上，对全局模式良好的图像也能完美地工作。此外，该模型可以重新表述为可分离凸优化问题，并具有分裂的性质，因此采用部分并行分裂法(partially parallel splitting method，PPSM)求解。一系列图像恢复的数值实验表明，在很多情况下，PPSM算法的迭代次数和计算时间都比现有的一些算法略短。
关键词：Cartoon–texture， Image decomposition， Low-rank， Convex optimization， Image restoration
1、引言
图像分解：
基于卡通纹理的图像恢复模型可以概括为(1)，即
其中𝑏0为观测图像，𝛷为线性退化算子，𝜀是已知方差的加性白噪声。由于退化矩阵𝛷的出现，这类问题是不适定的。
patch的一个完美特性是它们几乎是线性相关的，这意味着整个纹理patch集合应该是低秩的。然而LPR模型利用核范数全局获取块向量的低秩，即在每次迭代时同时优化整个纹理，这可能会出现全局特征。因此，当图像具有各种不同的纹理模式时，LPR模型对于图像分解不太理想。为了克服LPR模型的缺点，Ono等人[12]提出分块低秩模型来表征具有全局不同但局部良好模式的纹理。[12]中提出的模型的核心思想是利用所谓的块核范数(BNN)来表征纹理组件的局部块。[12]表明，当图像具有局部分块有序纹理时，他们的模型比LPR模型性能好。然而模型相对复杂，交替方向法(ADMM)可以有效地求解灰度图像的BNN模型，但在彩色图像上有些困难。
是否可以考虑一个简单的模型来描述全局模式的纹理结构，同时，该模型可以通过一种易于实现的算法进行有效求解。
本文提出简单有效的图像分解模型，该模型直接利用核范数和TV范数分别归纳给定图像的原始纹理分量和卡通分量。将提出的模型称为定制的低秩先验(Customized low-rank prior，CLRP)，以区分上述模型。
2.Notations
在本节中，我们总结了一些将在本文中使用的符号.
设𝑡> 0和𝒃∈R𝑛，著名的收缩算子“shrink(⋅，⋅)”(见[17])按组件方式定义
注意，收缩运算符也可用于矩阵。给定矩阵𝑋和标量𝑡> 0，让𝑋=𝑈𝛴𝑉⊤表示𝑋的奇异值分解(SVD)，然后定义软阈值算子(参见[18]) S∶R𝑚×𝑛→R𝑚×𝑛
3. 模型和算法
3.1. 定制低阶先验模型
文献中有充分的证据表明，直接最小化秩函数是NP-难的。因此，我们使用了广泛使用的秩函数的凸代理，即核范数，来提升纹理部分的低秩。
其中𝜏和𝜇是两个正则化参数，以平衡卡通和纹理组件。
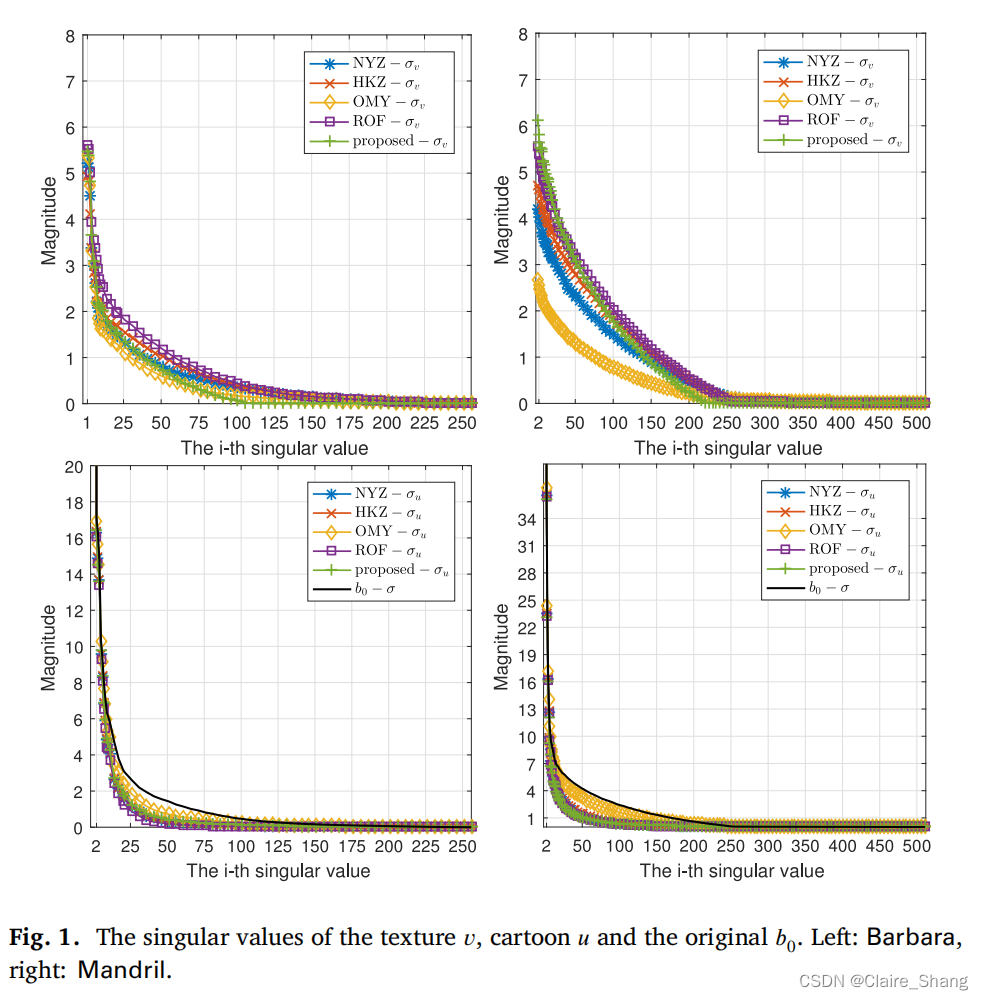
为了进一步说明纹理𝑣核范数的合理性，在图1绘制原始图像𝑏0的奇异值。可以看出，纹理部分的奇异值较小，卡通分量的奇异值较大，接近于𝑏0，这也意味着卡通部分𝑢包含图像𝑏0的主要信息。此外，我们可以观察到卡通部分和纹理部分都有近似的低秩(参见[19])。但是从图1的第一行可以看出，奇异值越小，对应的纹理越理想，例如“OMY”得到的纹理奇异值最小。因此，如果我们同时使用核范数来刻画卡通部分和纹理部分的近似低秩，纹理部分对应的较小奇异值可能会被截断，从而无法提取出理想的卡通部分和纹理部分。
3.2. 算法
CLRP模型是一个凸最小化问题，使用传统的优化方法求解这样一个非光滑模型并不容易，因此，引入两个辅助变量𝑦和𝑧，将▽𝑢和𝑢+𝑣从目标函数中分离出来
（7）的基准求解器是增广拉格朗日方法(ALM，)。然而，ALMt的直接应用于（7）可能会遇到耦合的非光滑子问题，从而容易实现，因为这种直接的ALM应用忽略了目标的有利可分结构。对于给定的𝑘th迭代(𝑣𝑘,𝑤𝑘,𝜆𝑘)，解耦ALM的子问题立即产生以下迭代方案:
(9)式最后一项的z难道不是错了吗，应该是w
𝜆称为与线性约束相关的拉格朗日乘子。注意，我们在(6)中有两个线性约束，拉格朗日乘数𝜆由两个块组成，即𝜆=(𝜆1，𝜆2), 其中𝜆1和𝜆2分别对应 ∇𝑢=𝑦 和 𝑢+𝑣=𝑧.
由于机器学习和图像处理中的高维特征，利用现代并行计算设备进行算法加速是值得称赞的。以并行的方式实现算法，同时更新(又称雅可比矩阵)算法优于顺序更新算法(也称为高斯-赛德尔)算法。
具体来说，PPSM到（6）的具体迭代方案如下： partially parallel splitting method (PPSM)
-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
PPSM:参考文献[16]. 下面的子问题推导我算了好久总是不太对，才意识到这个算法文中没有细说，翻了参考文献才发现是作者的另一篇文章，根据给出的算法直接代入就行，感兴趣再仔细研究算法吧。
原问题：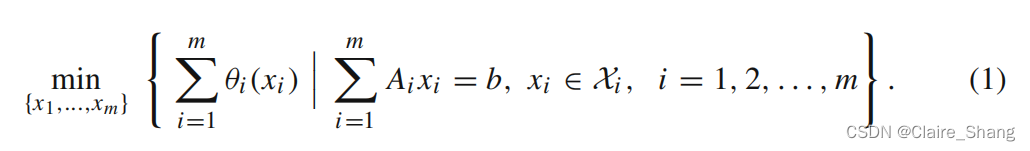
求解算法框架：
OMG！！！直接代入是不是超简单。要特别注意3和5，i=1和 i=2，....，m是不同的代入公式，要看清楚啊。一下午都在计算文中直接给出的子问题，结果白搞，还是老老实实查文章最重要啊。 ----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
- 选择合适的正常数𝑟和𝑠，有助于确定PPSM的收敛性。对松弛步骤取松弛因子𝛾∈(0,2)。
- Update 𝑢𝑘+1 via
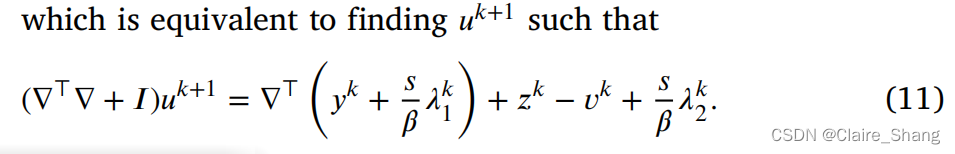利用FFT或DCT求解 - 计算𝜆̃𝑘
- Generate 𝑣̃𝑘 and 𝑤̃𝑘 simultaneously via
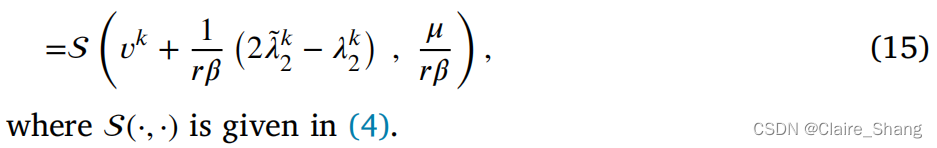
- With the notation ℎ(𝑤), the prediction on 𝑤̃ 𝑘 in (14) includes two completely separable subproblems on 𝑦 and 𝑧. Hence, we can also compute 𝑦̃ 𝑘 and𝑧 ̃𝑘 simultaneously.
求解线性方程组(17)的关键在于矩阵的结构𝛷. 一般情况下可以考虑三种情况：
- 若𝛷是恒等、对角或降采样矩阵，由于左侧的系数矩阵是对角的，可以直接求解；
- 若𝛷是由已知的空间不变点扩散函数生成的模糊矩阵，可以通过FFT或DCT求解该线性系统；
- 当𝛷是由模糊矩阵和降采样矩阵组成时，我们可以使用预条件共轭梯度法(PCG)来得到近似解，而不是精确解.
——— 元素取值都在[0,1]之间的矩阵叫模糊矩阵. 模糊矩阵 预条件共轭梯度法
算法归纳：
Remark 2. 正常数𝑟可以看作是一个一般的近端正则化参数来调整（14）中子问题的性质（参见（26）给出的矩阵𝑄）。很明显，我们可以看到这些（6）中的矩阵𝐵和𝐶都是满列秩。在这种情况下，我们可以建立全局收敛性和迭代复杂度。对于参数𝛾，理论上我们可以取𝛾∈(0,2)。在松弛步骤(或外推步骤)(18)中引入了这样一个常数，用于算法实现中的潜在加速度。根据经验，我们可以采用𝛾∈[1,2)来获得更好的性能。下面，我们证明算法1是全局收敛的，并且对本文完备性具有O(1∕𝑡) 的收敛速度，其中𝑡是迭代计数器。
注意，解决凸问题（7）相当于找到以下最大-最小问题的鞍点
其中L0(𝑢, 𝑣, 𝑤, 𝜆) 由(9)定义，𝛽= 0对应于(7)的拉格朗日函数. 显然，鞍点问题（19）等价于混合变分不等式(MVI)问题,表示为MVI（𝛺，𝐹，𝜃）：find 𝝃∗=（𝑢∗，𝑣∗，𝑤∗，𝜆∗）∈𝛺 使得
这里还有一些定理和证明，我就不放了。主要是借鉴了 参考文献[26] . 改天再认真看.
Remark 3. 定理1的第一项表示算法1生成的序列{(𝑢𝑘，𝑣𝑘，𝑤𝑘)}全局收敛于（7）的一个解。此外，(ii)项表示PPSM最差案例O(1∕𝑡）的收敛速度。
4.实验结果
测试四个案例
(i)干净图像分解，设置𝛷=𝑰，𝑰为恒等算子;
(ii)图像修复，取𝛷=𝑺，𝑺是二进制“掩码”(即下采样矩阵)，对应于分割缺少信息的图像(即像素);
(iii)图像去模糊，指定𝛷=𝑩，𝑩为已知的模糊矩阵;
(iv)图像去模糊和修复，设置𝛷=𝑺𝑩，这是去模糊矩阵和下采样矩阵的复合算子. 在算法1的算法实现中，算法中提到的参数𝑟、𝑠、𝛾定为1.00、2.01、1.60，
停止条件：
4.1. Clear image decomposition: 𝛷 =I
4.2. Image inpainting: 𝛷 = S
信噪比：
其中𝑏̃是一个重建的图像，𝑏是地面真值。让𝑏0，𝑢，𝑣分别表示观察到的图像，卡通和纹理。
4.3. Image deblurring: 𝛷 = 𝑩
4.4. Image deblurring and inpainting: 𝛷 = 𝑺𝑩
5.总结
提出了一种基于卡通纹理的低秩纹理先验图像分解模型。使用完整的核范数来表征纹理成分。采用一种具有保证收敛性的PPSM算法求解该模型。数值计算结果表明了所提模型的有效性和所采用算法的有效性。我们发现，当图像具有全局良好模式时，所提出的模型可以很好地进行纯卡通纹理图像分解。然而，在现实中，噪声图像是很常见的。粗略地说，基于卡通纹理的模型对噪声图像的处理具有挑战性，因为噪声具有振荡成分。因此，如何从具有高阶噪声的图像中提取卡通和纹理成分是我们未来的工作。此外，为了提高分解的质量，我们还将进一步关注非凸模型。
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
