题目链接:Periodic Signal
题意:求
思路:
求题目所给的最小值转化为了求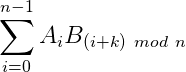
构造序列两个
求这两个序列的卷积,就可以得到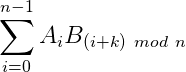
求卷积用fft来实现,复杂度为o(n*log(n))
由于用fft算出来的数精度误差会比较大,可以用这个方法先算出k的位置,然后将k代入原始式子,求得答案。
代码:
# pragma comment(linker, "/STACK:1024000000,1024000000")
# include <iostream>
# include <algorithm>
# include <cstdio>
# include <cstring>
# include <cmath>
using namespace std;
typedef long long ll;
const long double PI = acos(-1.0);
const int maxn = 5e5 + 5;
int a[maxn], b[maxn];
int n;
struct Complex {
long double x, y;
Complex() : x(0.0), y(0.0) { }
Complex(long double x, long double y) : x(x), y(y) { }
Complex operator - (const Complex &b) const {
return Complex(x - b.x, y - b.y);
}
Complex operator + (const Complex &b) const {
return Complex(x + b.x, y + b.y);
}
Complex operator * (const Complex &b) const {
return Complex(x * b.x - y * b.y, x * b.y + y * b.x);
}
} A[maxn], B[maxn];
void change(Complex y[], int len) {
int i, j, k;
for (i = 1, j = len / 2; i < len - 1; i++) {
if (i < j) swap(y[i], y[j]);
k = len / 2;
while (j >= k) {
j -= k; k /= 2;
}
if (j < k) j += k;
}
}
void fft(Complex y[], int len, int on) {
change(y, len);
for (int h = 2; h <= len; h <<= 1) {
Complex wn(cos(-on * 2 * PI / h), sin(-on * 2 * PI / h));
for (int j = 0; j < len; j += h) {
Complex w(1, 0);
for (int k = j; k < j + h / 2; k++) {
Complex u = y[k];
Complex t = w * y[k + h / 2];
y[k] = u + t;
y[k + h / 2] = u - t;
w = w * wn;
}
}
}
if(on == -1)
for (int i = 0; i < len; i++) y[i].x /= len;
}
ll sqr(ll x) {
return x * x;
}
int main(void)
{
int T; scanf("%d", &T);
while (T-- && scanf("%d", &n)) {
for (int i = 0; i < n; ++i) {
scanf("%d", a + i);
A[i] = Complex(a[i] * 1.0, 0.0);
}
for (int i = 0; i < n; ++i) {
scanf("%d", b + i);
B[n - i - 1] = Complex(b[i] * 1.0, 0.0);
}
for (int i = n; i < n * 2; ++i) B[i] = B[i - n], A[i] = Complex(0.0, 0.0);
n *= 2;
int len = 1;
while (len < n) len <<= 1;
len <<= 1;
for (int i = n; i < len; ++i) A[i] = B[i] = Complex(0.0, 0.0);
fft(A, len, 1); fft(B, len, 1);
for (int i = 0; i < len; ++i) A[i] = A[i] * B[i];
fft(A, len, -1);
int k = 0;
long double Max = A[n * 2 - 1].x;
n /= 2;
for (int i = n * 2 - 2; i >= n; --i) {
if (Max < A[i].x) {
Max = A[i].x; k = n * 2 - i - 1;
}
}
ll ans = 0;
for (int i = 0; i < n; ++i) {
ans += sqr(a[i] - b[(i + k) % n]);
}
printf("%lld\n", ans);
}
return 0;
}







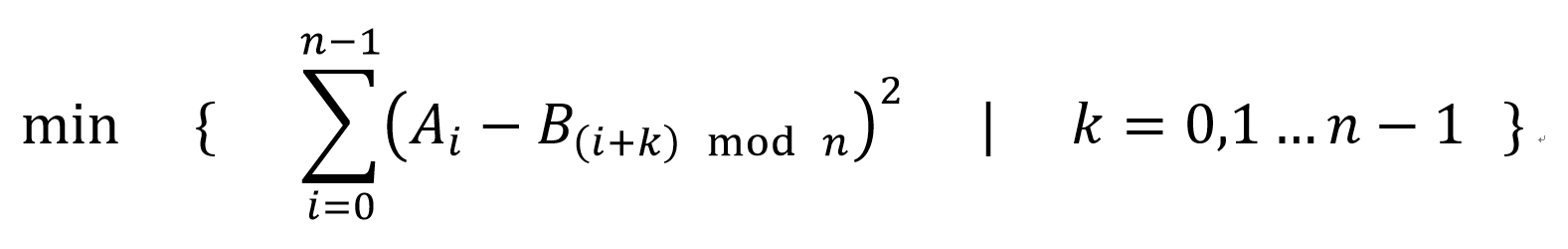
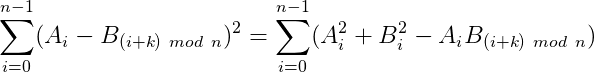
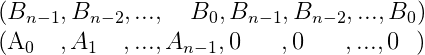














 393
393

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








