复分析——第10章——Θ函数应用(E.M. Stein & R. Shakarchi)

本文链接：https://blog.csdn.net/ComputerInBook/article/details/140070121

第10章 Θ函数的应用

(Applications of Theta Functions)

The problem of the representation of an integer n as

the sum of a given number k of integral squares is one

of the most celebrated in the theory of numbers. Its

history may be traced back to Diophantus, but begins

effectively with Girard’s (or Fermat’s) theorem that a

prime 4m + 1 is the sum of two squares. Almost every

arithmetician of note since Fermat has contributed to

the solution of the problem, and it has its puzzles for

us still. (将整数 n 表示为给定数量 k 的整数平方之和的问题是数论中最著名的问题之一。它的历史可以追溯到Diophantus(译注：古希腊数学家)，但实际上始于Girard (或Fermat)定理，即素数 4m + 1 是两个平方和。自Fermat以来几乎每一位著名的算术家都对这个问题的解决做出了贡献，但它仍然给我们带来了困惑。)

--------------------------------------------------------------- G.H. Hardy, 1952

本章将详细介绍 Θ 函数的理论及其在组合数学(combinatorics)和数论中的一些应用。

Θ 函数由级数

$\displaystyle \Theta(z|\tau) = \sum_{-\infty}^{\infty}e^{{\pi}{in^{2}\tau}} e^{2{\pi}inz}$

给出，其对于任意 z∈ℂ 和上半平面中的 𝒯 收敛。

Θ函数的一个显著特征是它的对偶性(dual nature)。当将其视为 z 的函数时，我们会在椭圆函数的“舞台”(arena)中看到它，因为 Θ 是周期性的，具有周期为 1 且“半周期(quasi-period)”𝒯。当被视为 𝒯 函数时，Θ 揭示了其模块化性质和配分函数(partition function)以及将整数表示为平方和的问题的密切联系。

允许我们利用这些联系的两个主要工具是Θ的三重积(tripleproduct)及其变换定律。一旦我们证明了这些定理，我们就会简要介绍其与配分的联系，然后转向有关将整数表示为两个或四个平方和的著名定理的证明。

1. Jacobi[dʒəkóubi] Θ 函数乘积公式(Product formula for the Jacobi theta function)

对于z∈ℂ 和 𝒯∈ℍ，Jacobi Θ 函数以其最精致的形式被定义为

(1) $\displaystyle \Theta(z|\tau) = \sum_{-\infty}^{\infty}e^{{\pi}{in^{2}\tau}} e^{2{\pi}inz}$ 。

两个重要的特例(或变化)是θ(𝒯)和ϑ (t)(译注：ϑ是θ的数学斜体写法，LaTex语法“\vartheta”),分别被定义为

$\displaystyle \theta(\tau) = \sum_{-\infty}^{\infty}e^{{\pi}{in^{2}\tau}} (\tau \in \mathbb{H})$ ，

$\displaystyle \vartheta(\tau) = \sum_{-\infty}^{\infty}e^{-{\pi}{n^{2}\tau}} (\tau \in \mathbb{H})(t>0)$ 。

事实上，这些各种函数之间的关系是由θ(𝒯) = Θ(z|0) 和 ϑ (t) = θ(it)( t > 0 )给出的。

我们已经多次遇到过这些函数。例如，在研究圆的热扩散方程时(在第I册书的第 4 章中),我们求得热传导核为

$\displaystyle H_{t}(x) = \sum_{n=-\infty}^{\infty}e^{-4{\pi}^{2} n^{2}t}e^{2{\pi}inx}$ ，

因此， $H_{t}(x) = \Theta(x|4{\pi}it)$ 。

另一个例子是ζ函数研究中ϑ 的出现。事实上，我们在第 6 章证明了ϑ 的函数方程隐含了ζ 的函数方程，从而导致了 ζ 函数的解析延拓。

我们从仔细研究θ作为z 的函数(固定 𝒯 )开始，通过记录其基本结构特性进行研究，这种基本结构这在很大程度上刻画这个函数。

命题 1.1 函数Θ 满足下列属性：

( i ) Θ 在 z∈ℂ 中是复可积的，并且在 𝒯∈ℍ 中是全纯的。

( ii ) Θ(z + 1|𝒯 ) = Θ(z|𝒯) 。

( iii ) $\displaystyle \Theta(z + \tau|\tau ) = \Theta(z|\tau)e^{-{\pi}i\tau} e^{-2{\pi}iz}$ 。

( iv ) Θ(z|𝒯 ) = 0 (只要 z = 1/2 + 𝒯/2 + n + m 𝒯 且 n，m∈ℤ )。

证明：

假设 $\mathrm{Im}(\tau) = t \ge t_{0} > 0$ 和 z = x + iy 属于 ℂ 中的有界集(比如，| z| ≤ M )。则，定义Θ 的级数绝对且一致收敛，因为

$\displaystyle \sum_{n=-\infty}^{\infty}|e^{{\pi}in^{2}\tau} e^{2{\pi}inz} | \le C \sum_{n \ge 0}e^{-{\pi}n^{2}t_{0}}e^{2{\pi}nM} < \infty$ 。

因此，对于每一个固定的 𝒯∈ℍ ，函数Θ(.|𝒯 )是复可积的，对于每一个固定的 z∈ℂ ，函数Θ(z|.)在上半平面上是全纯的。

由于指数函数 $e^{2{\pi}inz}$ 是以 1 为周期的周期函数，从Θ的定义立即可得出属性( ii )。

为了证明第 ( iii ) 个属性，我们可以使Θ(z + 𝒯|𝒯 )的表达式中的平方完整。具体说来，我们有

$\begin{array}{rlc} \displaystyle \Theta(z + \tau|\tau ) = &\displaystyle \sum_{n=-\infty}^{\infty}e^{{\pi}in^{2}\tau}e^{2{\pi}in(z+\tau)} \\ \\ =&\displaystyle \sum_{n=-\infty}^{\infty}e^{{\pi}i(n^{2}+2n)\tau}e^{2{\pi}inz} \\ \\ =&\displaystyle \sum_{n=-\infty}^{\infty}e^{{\pi}i(n+1)^{2}\tau}e^{-{\pi}i\tau}e^{2{\pi}inz} \\ \\ =&\displaystyle \sum_{n=-\infty}^{\infty}e^{{\pi}i(n+1)^{2}\tau}e^{-{\pi}i\tau}e^{2{\pi}i(n+1)z}e^{-2{\pi}iz} \\ \\ =&\displaystyle \Theta(z|\tau) e^{-{\pi}i\tau}e^{-2{\pi}iz} \end{array}$ 。

因此，我们看到Θ(z|𝒯 )作为 z 的函数，是具有 1 为周期和以 𝒯 为“半周期”的周期函数。

为了建立最后一个属性，根据刚才的证明方法，只需证明 Θ(1/2 + 𝒯/2|𝒯 ) = 0 即可。我们再次使用 n 与 $n^{2}$ 之间的相互作用得到

$\begin{array}{rlc} \Theta(1/2 + \tau/2|\tau ) = &\displaystyle \sum_{-\infty}^{\infty}e^{{\pi}in^{2}\tau} e^{2{\pi}in(z/2+\tau/2)} \\ \\ =&\displaystyle \sum_{-\infty}^{\infty}{(-1)}^{n} e^{{\pi}i(n^{2}+n)\tau} \end{array}$ 。

为了看出这最后一项和恒为0 ,只需使 n ≥ 0 与 –n – 1 相匹配即可，我们观察到它们具有相反的部分， $(-n-1)^{2} + (-n -1) = n^{2} + n$ 。这就完成了对命题的证明。接下来我们考虑一个与Θ(z|𝒯 )共享相同结构属性并同样作为 z 的函数的乘积 $\prod{(z|\tau)}$ 。对于z∈ℂ 和 𝒯∈ℍ，这个函数被定义为

$\displaystyle \prod(z ,\tau) = \prod_{n=1}^{\infty}(1-q^{2n} ) (1+q^{2n-1} e^{2{\pi}iz)}(1+q^{2n-1} e^{-2{\pi}iz})$ ，

其中，我们使用了业内标准的记法，即 $q = e^{{\pi}i\tau}$ 。函数 $\prod{(z|\tau)}$ 有时候也称为三重积(triple-product)。

命题 1.2 函数 $\prod{(z|\tau)}$ 满足下列的属性：

( i ) Π(z ,𝒯) 在 z∈ℂ 中是复可积的，并且在 𝒯∈ℍ 中是全纯的。

( ii ) Π(z + 1|𝒯 ) = Π(z|𝒯) 。

( iii ) $\prod(z + \tau|\tau ) = \prod(z|\tau)e^{-{\pi}i\tau} e^{-2{\pi}iz}$ 。

( iv ) Π(z|𝒯 ) = 0 (只要 z = 1/2 + 𝒯/2 + n + m 𝒯 且 n，m∈ℤ )。此外，这些点是Π(.|𝒯 ) 的简单极点，且Π(.|𝒯 ) 没有其它零点。

证明：

假设 $\mathrm{Im}(\tau) = t \ge t_{0} > 0$ 和 $z = x + iy$ ，则 $|q|\le e^{-{\pi}t_{0}} < 1$ 和

$\displaystyle (1-q^{2n} )(1+q^{2n-1} e^{2{\pi}iz})(1+q^{2n-1} e^{-2{\pi}iz}) = 1 + O(|q|^{2n-1} e^{2{\pi}|z|})$ 。

由于级数 $\sum{|q|^{2n-1} }$ 收敛，第5章中无穷级结论确保了 Π(z|𝒯 ) 定义了一个 z 的复可积函数(𝒯∈ℍ固定)，以及定义了 𝒯∈ℍ 的一个全纯函数( z∈ℂ固定)。

此外，显然，从定义可看出Π(z|𝒯 )是以z为自变量以 1 为周期的周期函数。

为了证明第三个属性，我们首先注意到，由于 $q^{2}=e^{2{\pi}i\tau}$ ，我们有

$\begin{array}{rlc} \displaystyle \prod( z + \tau|\tau) =&\displaystyle \prod_{n=1}^{\infty}(1-q^{2n}) (1+q^{2n-1} e^{2{\pi}i(z + \tau)})(1+q^{2n-1} e^{-2{\pi}i(z + \tau)}) \\ \\ =&\displaystyle \prod_{n=1}^{\infty}(1-q^{2n}) (1+q^{2n+1} e^{2{\pi}iz})(1+q^{2n-3} e^{-2{\pi}iz}) \end{array}$ 。

对比最后一个积和 Π(z ,𝒯)并隔离缺失或额外因子，就导出了

$\displaystyle \prod( z + \tau|\tau) =\prod(z|\tau)\left ( \frac{1+q^{-1} e^{-2{\pi}iz}}{1+qe^{{2\pi}iz }{}} \right )$ 。

因此，( iii )可证，因为 $(1 + x )/(1 + x^{-1})= x$ (只要 x ≠ -1)。

最后，为了求得Π(z|𝒯 )的零点，我回顾一下，一个收敛积仅当至少其因子之一是0时其消没。显然，因子 $(1 - q^{n})$ 永远不会消没，因为|q| < 1 。这第二个因子 $(1 - q^{2n-1} e^{2{\pi}iz})$ 当 $q^{2n-1} e^{2{\pi}iz}=-1=e^{{\pi}i}$ 时消没。由于 $q = e^{{\pi}i\tau}$ ，则我们有(注：我们使用标准速记，a = b (mod c) 指的是 a – b 是 c 的整数倍)

(2n - 1)𝒯 + 2z = 1 (mod 2)。

因此，

z = 1/2 + 𝒯/2 – n𝒯 (mod 1),

这就处理了 1/2 + 𝒯/2 - n 𝒯 + m 这种类型的零点(n ≥ 1 且 m∈ℤ)。类似地，若

(2n - 1)𝒯 - 2z = 1 (mod 2)

则第三个因子消没，这意味着

$\begin{array}{rlc}z =& -1/2 - \tau/2 + n\tau (\mathrm{mod}\: 1) \\ \\ =& 1/2 + \tau/2 + n^{'}\tau (\mathrm{mod}\: 1), \end{array}$

其中， $n^{'} \ge 0$ 。这就穷尽了Π(.|𝒯 )的零点。最后，这些零点是简单零点，因为函数 $e^{w}-1$

在原点消没至 1 阶(从幂级数展开或简单微分中显而易见的事实)。

乘积 Π 的重要性源自以下称为Θ 乘积公式的定理。函数 Θ(z|𝒯)和Π(z|𝒯 )满足相似属性的事实暗示了两者之间的密切联系。情况确实如此。

定理 1.3 (乘积公式) 对于z∈ℂ 和 𝒯∈ℍ，我们有恒等式 Θ(z|𝒯) = Π(z|𝒯 ) 。

证明：

固定 𝒯∈ℍ 。我们首先断言(claim)存在一个常量 c(𝒯)使得

(2) Θ(z|𝒯 ) = c(𝒯) Π(z|𝒯 ) 。

事实上，考虑商 F(z) = Θ(z|𝒯 )/ Π(z|𝒯 )，并注意到，根据前面的两个命题，函数 F(z) 是复可积的，并且是以 1 和 𝒯 为周期的双周期函数。这意味着 F 就是所断言的常量。

现在，我们必须证明对于任意 𝒯，c(𝒯) = 1 ，且要点是建立 c(𝒯) = c(4𝒯) 。若我们在 (2) 中置 z = 1/2 , 则 $e^{-2{\pi}iz}=-1$ , 我们求得

$\begin{array}{rlc} \displaystyle \sum_{n=-\infty}^{\infty}(-1)^{n} q^{n^{2}} =&\displaystyle c(\tau) \prod_{n=1}^{\infty}(1-q^{2n}) (1-q^{2n-1})(1-q^{2n-1}) \\ \\ =&\displaystyle c(\tau) \prod_{n=1}^{\infty}\left [(1-q^{2n-1}) (1-q^{2n}) \right ](1-q^{2n-1}) \\ \\ =&\displaystyle c(\tau) \prod_{n=1}^{\infty}(1-q^{n})(1-q^{2n-1}) \end{array}$ 。

因此，

(3) $\displaystyle c(\tau)=\frac{\displaystyle \sum_{n=-\infty}^{\infty}(-1)^{n} q^{n^{2}} }{\displaystyle \prod_{n=1}^{\infty}(1-q^{n})(1-q^{2n-1}) }$ 。

接下来，我们在 (2) 中置 z = 1/4 , 因此 $e^{2{\pi}iz}=-i$ ，则只有 n = 偶数 = 2m 的项不被抵消；因此

$\displaystyle \Theta(1/4|\tau ) = \sum_{m=-\infty}^{\infty}q^{4m^{2}}(-1)^{m}$ 。

在另一方面，

$\begin{array}{rlc} \displaystyle \prod{(1/4|\tau)} =&\displaystyle \prod_{m=1}^{\infty}(1-q^{2m}) (1+iq^{2m-1})(1-iq^{2m-1}) \\ \\ =&\displaystyle \prod_{m=1}^{\infty}(1-q^{2m}) (1+q^{4m-2}) \\ \\ =&\displaystyle \prod_{n=1}^{\infty}(1-q^{4n})(1-q^{8n-4}) \end{array}$ ，

其中，最后的一行是通过分别考虑第一个因子中的两种情况 2m = 4n - 4 和 2m = 4n - 2 获得的。因此，

(4) $\displaystyle c(\tau)=\frac{\displaystyle \sum_{n=-\infty}^{\infty}(-1)^{n} q^{4n^{2}} }{\displaystyle \prod_{n=1}^{\infty}(1-q^{4n})(1-q^{8n-4}) }$ ,

将 (3) 和 (4) 组合在一起，就建立了我们的断言 c(𝒯) = c(4𝒯) 。连续应用这个恒等式就得到 $c(\tau) = c(4^{k\tau})$ ，由于当 k ⟶ ∞ 时， $q^{4^{k}} = e^{i{\pi}4^{k}\tau} \rightarrow 0$ ，这就提供了θ在上半平面是非消没的一个证明。

推论 1.4 若 Im(𝒯) > 0 和 $q = e^{{\pi}i\tau}$ ，则

$\displaystyle \theta(\tau) = \prod_{n=1}^{\infty}(1-q^{2n} )(1+q^{2n-1})^{2}$ 。

因此，对于 𝒯∈ℍ ，θ(𝒯) ≠ 0 。

下一个推论证明了Θ 函数的属性可产生椭圆函数的结构(事实上，其与 Weierstrass ℘ 函数密切相关)(译注：符号“℘”读作“Weierstrass p”，的Unicode为02118 ，LaTex语法为“\wp)。

推论 1.5 对于每一个固定的 𝒯∈ℍ ，商

$\displaystyle (\log{\Theta(z|\tau)})^{''}=\frac{\Theta(z|\tau)\Theta^{''}(z|\tau)-(\Theta^{'}(z|\tau))^{2}}{(\Theta(z|\tau))^{2}}$

是一个以 1 和 𝒯 为周期 2 阶椭圆函数，且在 z = 1/2 + 𝒯/2 处具有一个双极点。

在上面的表达式中，上标符号( ’)表示对 z 变量的微分。微分命题 1.1 中的恒等式(ii) 和 (iii) 就给出 F(z + 1) = F(z) 和 F(z + 𝒯 ) = F(z) – 2πi ，再一次微分就证明了 $F^{'}$ 是双周期的。由于Θ(z|𝒯 ) 在基础平行四边形中仅在 z = 1/2 + 𝒯/2 处消没，因此函数 F(z) 仅有一个单独的极点，因此函数 $F^{'}$ 在这个点处仅有一个双极点。

$\displaystyle (\log{\Theta(z|\tau)})^{''}$ 和 $\wp_{\tau}(z)$ 之间的准确联系见练习 1 所述。

对于 Θ 函数和Weierstrass ℘ 函数之间的类比，见前一章练习 5 。

1.1 深入变换定律(Further transformation laws)

现在我们来研究 𝒯 变量的变换关系，即研究Θ的模特征(modular character)。

回顾一下，在前一章中，Weierstrass ℘ 函数和 Eisenstein 级数 $E_{k}$ 通过两个变换

𝒯 ⟼ 𝒯 + 1 和 𝒯 ⟼ -1/𝒯

所反映出来，其保留了上半平面。在接下来的过程中，我们将分别使用 $T_{1}$ 和 S 表示这两个变换。

然而，当考察 Θ 函数的时候，很自然地会考虑用另外两个变换替代去分析，即考虑

$T_{2} :\tau \mapsto \tau + 2$ 和 $S :\tau \mapsto -1/\tau$ ，

因为Θ(z| 𝒯 + 2) = Θ(z| 𝒯) ，但Θ(z| 𝒯 + 1) ≠ Θ(z| 𝒯) 。

我们的首要任务是学习在映射 𝒯 ⟼ -1/𝒯 下Θ(z| 𝒯)的变换。

定理 1.6 若 𝒯∈ℍ，则

(5) $\displaystyle \Theta(z|-1/\tau) = \sqrt{\frac{\tau}{i}}e^{{\pi}i\tau}z^{2}\Theta(z\tau|\tau)$ (对任意 z∈ℂ )。

$\sqrt{\tau/i}$ 在此表示定义在上半平面的平方根的这个分支，当 𝒯 = it (t > 0)时它是正数。

证明：

只需针对实数 z = x 和 𝒯 = it (t > 0)证明这个公式即可，因为对于每一个固定的 x∈ℝ ，等式(5)的两边在上半平面都是调和函数，然后在正虚轴上一致，因此必然处处相等。此外，对于一个固定的 𝒯∈ℍ，以z为自变量所定义的调和函数的两边在实轴上一致，因此也必然处处相等。

根据 x 是实数和 𝒯 = it (t > 0) ，则公式变成

$\displaystyle \sum_{n=-\infty}^{\infty}e^{-{\pi}n^{2}/t}e^{2{\pi}inx}=t^{1/2}e^{-{\pi}tx^{2}}\sum_{n=-\infty}^{\infty}e^{-{\pi}n^{2}t}e^{-2{\pi}nxt}$ 。

用 a 替换 x，我们发现我们必须证明

$\displaystyle \sum_{n=-\infty}^{\infty}e^{-{\pi}t(n+a)^{2}}=\sum_{n=-\infty}^{\infty}t^{1/2}e^{-{\pi}n^{2}/t}e^{2{\pi}ina}$ 。

然而，这正是第四章中的等式(3)，它是由Poisson求和公式推导出来的。

特别是，通过在定理中设 z = 0 ，我们求得下面的推论。

推论 1.7 若Im(𝒯) > 0 , 则 $\theta(-1/\tau) = \sqrt{\tau/i}\theta(\tau)$ 。

注意，若 𝒯 = it, 则 θ(𝒯) = ϑ(t) ，上述关系式恰好是在第 4 章中出现过的 ϑ 函数方程。

变换定律 $\theta(-1/\tau) = (\tau/i)^{1/2}\theta(\tau)$ 给到我们关于当 𝒯 ⟶ 0 时行为的准确信息。下一个推论在后面会用到(当我们需要分析随着 𝒯 ⟶ 1 时的θ(𝒯)的行为时)。

推论 1.8 若 Im(𝒯) > 0 , 则 $\theta(-1/\tau) = \sqrt{\tau/i}\theta(\tau)$ 。

若 𝒯∈ℍ，则

$\begin{array}{rlc}\displaystyle \theta(1 - 1/\tau) =&\displaystyle \sqrt{\frac{\tau}{i}}\sum_{n=-\infty}^{\infty}e^{{\pi}i(n+1/2)^{2}\tau} \\ \\ =&\displaystyle \sqrt{\frac{\tau}{i}}(2e^{{\pi}i\tau/4}+...) \end{array}$ 。

第二个恒等式意味着随着 Im(𝒯) ⟶ ∞ 而 $\theta(1 - 1/\tau) \sim \sqrt{\tau/i} 2e^{{\pi}i{\tau}/4}$ 。

证明：

首先我们注意到， $n$ 和 $n^{2}$ 具有相同的部分，因此

$\displaystyle \theta(1 + \tau) = \sum_{n=-\infty}^{\infty}(-1)^{n}e^{{\pi}in^{2}\tau} = \Theta(1/2|\tau)$ ，

故而，θ (1 - 1/ 𝒯) = Θ(1/2|-1/𝒯 )。接下来，我们利用取值 z = 1/2 的定理 1.6 ，则结果是

$\begin{array}{rlc} \displaystyle \theta(1 - 1/\tau) = &\displaystyle \sqrt{\frac{\tau}{i}}e^{{\pi}i\tau/4}\Theta(\tau/2|\tau) \\ \\ =&\displaystyle \sqrt{\frac{\tau}{i}}e^{{\pi}i\tau/4}\sum_{n=\infty}^{\infty}e^{{\pi}in^{2}\tau}e^{{\pi}int} \\ \\ =&\displaystyle \sqrt{\frac{\tau}{i}}\sum_{n=\infty}^{\infty}e^{{\pi}i(n+1/2)^{2}\tau} \end{array}$ 。

对应 n = 0 和 n = -1 的项贡献了 $2e^{{\pi}i\tau/4}$ 的项，其具有绝对值 $2e^{-{\pi}t/4}$ (其中 𝒯 = σ + it)。最后，其它 n ≠ 0 和 n ≠ -1 项的和是阶

$\displaystyle O \left (\sum_{k=0}^{\infty}e^{-(k+1/2)^{2}{\pi}t} \right ) = O \left (\sum_{k=0}^{\infty}e^{-9{\pi}t/4} \right )$ 。

我们的变换定律的最终推论从属于 Dedekind[déidəkint] η 函数，对于 Im(𝒯) > 0 ，定义为

$\displaystyle \eta(\tau) = e^{\frac{{\pi}iT}{12}}\prod_{n=1}^{\infty}(1-e^{2{\pi}in\tau} )$ 。

下面给出的 η 函数方程将与我们对四平方定理和分割理论的讨论相关。

命题 1.9 若 Im(𝒯) > 0 ，则 $\eta(-1/\tau) = \sqrt{\tau/i}\eta(\tau)$ 。

这个恒等式是通过对定理1.6中的关系式进行微分并在 $z_{0} = 1/2 + \tau/2$ 处计算所得。细节如下。

证明：

从Θ函数的乘积公式出发，我们可以用 $q = e^{{\pi}i\tau }$ 书写，

$\displaystyle \Theta(z|\tau) = (1 + qe^{-2{\pi}iz})\prod_{n=1}^{\infty}(1-q^{2n}) (1+q^{2n-1} e^{2{\pi}iz})(1+q^{2n+1} e^{-2{\pi}iz})$ ，

由于第一个因子在 $z_{0} = 1/2 + \tau/2$ 处消没，所以我们看到

$\Theta^{'}(z_{0}|\tau) = 2{\pi}i H(\tau)$ (其中， $\displaystyle H(\tau) = \prod_{n=1}^{\infty}(1-e^{2{\pi}in\tau} )^{3}$ ) 。

接下来我们观察到，在(5)中我们用 𝒯 替代 -1/𝒯 ，我们得到

$\displaystyle \Theta(z|\tau) = \sqrt{i/\tau} e^{-{\pi}iz^{2}/\tau}\Theta{(-z/\tau|-1/\tau)}$ 。

若我们对上述表达式进行微分，并在 $z_{0} = 1/2 + \tau/2$ 处进行计算，我们求得

$\displaystyle 2{\pi}i H(\tau) = \sqrt{i/\tau}e^{-\frac{{\pi}i}{4\tau}}e^{-\frac{{\pi}i}{2}}e^{-\frac{{\pi}i\tau}{4}}\left (\frac{-2{\pi}i}{\tau} \right )H(-1/\tau)$ 。

因此，

$\displaystyle e^{ \frac{{\pi}i\tau}{4}}H(\tau)= \left (\frac{i}{\tau} \right )^{3/2}e^{-\frac{{\pi}i}{4\tau}}H(-1/\tau)$ 。

当 𝒯 = it ( t > 0 )时，函数 η(𝒯) 是正的，因此，取上述表达式的立方根就给出 $\eta(-1/\tau) = \sqrt{\tau/i}\:{\eta(\tau)}$ ；因此，根据解析延拓性，对于任意 𝒯∈ℍ ，这个恒等式成立。

函数η和椭圆函数理论之间的关系在问题 5 中给出。

2. 生成函数(Generating functions)

已经一个序列 $\{F_{n}\}_{n=0}^{\infty}$ ，它可能以组合、递归或某些数论定律的形式出现，研究它的一个重要手段是研究其生成函数(generating function)，其被定义为

$\displaystyle F_{n}=\sum_{n=0}^{\infty}F_{n}x^{n}$ 。

很多时候，定义序列 $\{F_{n}\}$ 的属性包含函数 F(x) 有趣的代数或分析属性，研究这些属生最终将我们引回到关于序列 $\{F_{n}\}$ 的新的见解。Fibonacci[fi:bouná:ttʃi](译注：全名 Leonardo Pisano ,Fibonacci, Leonardo Bigollo，公元1175年-1250年,意大利数学家)数列给出了一个非常简单的例子。(参见练习 2 )。在这里，我们想要研究这个思想的一些不太基本的例子，与Θ函数相关。

我们首先非常简化地简单一下分割理论(the theory of partitions)。

分割函数(partition function)定义为：若 n 是正整数，我们令 p (n) 表示 n 可被写成正整数之和的方式的数量。例如，p (1) = 1 和 p(2) = 2 (因为 2 = 2 + 0 = 1 + 1)。此外，p(3) = 3 (因为 3 = 3 + 0 = 2 + 1 = 1 + 1 + 1 )。我们令 p(0) = 1 ，并在下表中搜集 p(n)的更进一步的值。

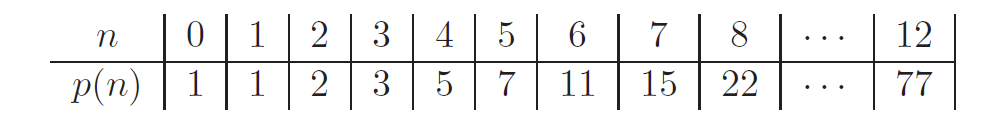
分割序列{ p(n) }的生成函数的第一个定理是 Euler恒等式。这不禁让人想起ζ函数的乘积公式。

定理 2.1 若 |x| < 1 ，则 $\displaystyle \sum_{n=0}^{\infty}p(n)x^{n} = \prod_{k=1}^{\infty}\frac{1}{1-x^{k}}$ 。

按规范格式，我们将每个分数写成

$\displaystyle \frac{1}{1-x^{k}} = \sum_{m=0}^{\infty}x^{km}$ ，

将这些展开以获得作为 $x^{n}$ 系数的 p(n)。事实上，当我们将相等的整数分组到 n 的分区中时，该分区可以写为

$n = m_{1} k_{1} + ... + m_{r} k_{r}$ ，

其中， $k_{1} ,..., k_{r}$ 是各不相同的正整数。这个分割对应的出现于乘积中的项

$(x^{k_{1}} )^{m_{1}} ... (x^{k_{r}} )^{m_{r}}$ 。

该形式论证的论证如 ζ 函数的乘积公式的证明一样进行(第 7 章第 1 节)；这是基于乘积 $\prod{1/(1-x^{k})}$ 的收敛性。而这个收敛性又推导自以下事实——对于每个固定的 |x| < 1 我们有

$\displaystyle \frac{1}{1-x^{k}}=1+O(x^{k})$ 。

类似的论证证明，乘积 $\prod{1/(1-x^{2n-1})}$ 等于 $p_{0}(n)$ (n 分割成奇数片的分割数)的生成函数。此外， $\prod{(1+x^{n})}$ 是 $p_{u}(n)$ ( n 分割成不等部分的分割数)的生成函数。显然，对于所有的n , $p_{0}(n)=p_{u}(n)$ ,并将其转换成恒等式

$\displaystyle \prod_{n=1}^{\infty}\left (\frac{1}{1-x^{2n-1}} \right )=\prod_{n=1}^{\infty}\left (1+x^{n} \right )$ 。

为了证明这一点，注意到 $(1 + x^{n})(1 - x^{n} ) = 1 - x^{2n}$ ，因此，

$\displaystyle \prod_{n=1}^{\infty} (1 + x^{n})\prod_{n=1}^{\infty} (1 - x^{n} ) =\prod_{n=1}^{\infty} (1 - x^{2n})$ 。

此外，考虑整数的奇偶数(parity)，我们有

$\displaystyle \prod_{n=1}^{\infty} (1 - x^{2n})\prod_{n=1}^{\infty} (1 - x^{2n-1} ) =\prod_{n=1}^{\infty} (1 - x^{n})$ ，

结合上述等式，就证明了预期的恒等式。

随后的命题更为深入，事实上，直接涉及到 Θ 函数。令 $p_{e,u}(n)$ 表示n分割成不等部分的偶数数量的分割数量，并令 $p_{o,u}(n)$ 表示n分割成不等部分的奇数数量的分割数量。则，Euler证明了，除非 n 是一个五角数(pentagonal number)，否则我们有 $p_{e,u}(n)=p_{o,u}(n)$ 。根据定义，五角数是形如 k(3k + 1)/2 (k∈ℤ)的整数 n 。(注：传统定义为：形如 n = k(k - 1)/2 的整数是“三角数(triangular numbers)”；形如 $n=k^{2}$ 的那些书称为“平方数(squares)”；形如 k(3k + 1)/2 的那些数称为“五角数(pentagonal number)。” 通常，形如(k/2)((l – 2)k + 𝓁 - 4)的数与 𝓁 边的多边形相关。) 例如，前面几个五角数是 1, 2, 5, 7, 12, 15, 22, 26, . . . 。事实上，若 n 是五角数，则

$p_{e,u}(n)=p_{o,u}(n)=(-1)^{k}$ (若 n = k(3k + 1)/2 )。

为了证明这个结论，我们首先注意到

$\displaystyle \prod_{n=1}^{\infty} (1 - x^{n})= \prod_{n=1}^{\infty}\bigg [ p_{e,u}(n)-p_{o,u}(n) \bigg ]x^{n}$ 。

这是可以推断的，因为在乘积中乘以这一项，我们就求得形如 $(-1)^{r} x^{n_{1}+...+n_{r}}$ 的项(其中， $n_{1},...,n_{r}$ 是各不相同的数)，n 分割成不等部分偶数数量的每一个分割 $n_{1} + ...+ n_{r}$ 贡献了 +1 (r 是偶数)，而n 分割成不等部分奇数数量的每一个分割 $n_{1} + ...+ n_{r}$ 贡献了 -1 (r 是奇数)。这准确地给出了系数 $p_{e,u}(n)-p_{o,u}(n)$ 。

通过上述恒等式，我们看到 Euler 定理是以下命题的结论。

命题 2.2 $\displaystyle \prod_{n=1}^{\infty} (1 - x^{n})= \sum_{n=-\infty}^{\infty}(-1)^{k}x^{\frac{k(3k+1)}{2}}$ 。

证明：

若我们设 $x=e^{2{\pi}iu}$ ，则我们可以写成

$\displaystyle \prod_{n=1}^{\infty} \bigg(1 - x^{n} \bigg )=\prod_{n=1}^{\infty} \bigg (1 - e^{2{\pi}inu} \bigg )$ 。

根据三重积

$\displaystyle \prod_{n=1}^{\infty}(1-q^{2n} ) (1+q^{2n-1} e^{2{\pi}iz})(1+q^{2n-1} e^{-2{\pi}iz})$

并令 $q = e^{3{\pi}iu}$ 和 $z = 1/2 + u/2$ ，我们得到

$\displaystyle \prod_{n=1}^{\infty}(1-e^{2{\pi}i3nu} ) (1-e^{2{\pi}i(3n-1)u}(1-e^{2{\pi}i(3n-2)u}) =\prod_{n=1}^{\infty}(1-e^{2{\pi}inu} )$ 。

根据定理 1.3 这个乘积等于

$\begin{array}{rlc}\displaystyle \prod_{n=-\infty}^{\infty}e^{3{\pi}in^{2}u}(-1)^{n}e^{2{\pi}inu/2} =&\displaystyle \prod_{n=-\infty}^{\infty}(-1)^{n} e^{{\pi}in(3n+1)u} \\ \\ =&\displaystyle \prod_{n=-\infty}^{\infty}(-1)^{n} e^{n(3n+1)/2} \end{array}$ ，

这就是所要证明的。

关于分割函数 p(n)我们做最后的评述。其随着 n ⟶∞ 的递增特征可以根据 $1/\prod_{n=1}^{\infty}(1-x)^{n}$

随着 |x| ⟶ 1 的行为进行分析。事实上，根据基本的考虑，我们可以根据随着 x ⟶ 1时生成函数的增长阶得到p(n)的大致的增长阶；参见练习 5 和 6。更精细的分析需要生成函数的变换属性，这可以追溯到相应的关于 η 的命题 1.9。这导出了一个非常好的p(n)的渐近公式。可以在附录 A 中找到。

3. 关于平方和的定理(The theorems about sums of squares)

古希腊人对作为直角三角形的三条边出现的三元组(a，b，c)着迷。它们是“Pythagoras三元组”，满足等式 $a^{2} + b^{2} = c^{2}$ 。根据Alexander 大帝时期的数学家Diophantus(大约公元 250年左右)的思想，若c是满足上述等式的那种类型的一个整数，且 a和b 没有公因子(我们很容易推导的一种情况)，则是 c 是某两个整数的平方和，即 $c = m^{2} + n^{2}$ (m，n ∈ℤ)；反之，任意这样的 c 都作为一个其边由Pythagoras三元组给出的直角三角形(triangle)的斜边(hypotenuse)出现。(参见练习 8 。) 因此，我们很自然地会问以下问题：哪些整数可以写成两个平方和？很容易看出，任何形如 4k + 3的数不可以这样写，但确定哪些整数可以用这种方式表示并不明显。

让我们以更定量的形式提出这个问题。我们定义 $r_{2}(n)$ 为可以将n写成两个数的平方和的方式的数量，统计明显重复；即， $r_{2}(n)$ 是使得

$n = x^{2} + y^{2}$

的数对(x ，y ) ( x，y ∈ℤ)的数量。例如， $r_{2}(3) = 0$ , 但 $r_{2}(5) = 0$ ，因为 $5 = (\pm2)^{2} + (\pm1)^{2}$ ，并且 $5 = (\pm 1)^{2} + (\pm 2)^{2}$ 。因此，我们的第一个问题可以按如下提出：

两个数的平方和：哪些整数可以被写成两个整数的平方和？更准确地说，我们可以确定 $r_{2}(n)$ 的表达式吗？

接下来，由于并非每个正整数都可以表示为两个整数的平方和，因此我们可能会问是三个整数的平方或四个整数的平方是否足够。然而，事实是有无限多个整数不能写成三个整数的平方和，因为很容易验证，没有一个形如 8k + 7 的整数可以写成三个整数的平方和。因此，我们转向四个整数的平方和问题，按照与 $r_{2}(n)$ 的类比，其 $r_{4}(n)$ 定义为将 n 表示为四个整数的平方和的方式数量。因此，出现的第二个问题是：

四个数的平方和：每一个整数都可以被写成四个整数的平方和吗？更准确地说，我们可以确定 $r_{4}(n)$ 的公式吗？

事实证明，追溯到三世纪的二个整数平方和四个整数平方和问题直到大约1500年后才得到解决，而它们的完整解决方案首先是通过使用Jacobi的Θ函数理论给出的！

3.1 两整数平方定理(The two-squares theorem)

将整数表示为两个整数的平方和的问题虽然在本质上显然是加法，但具有很好的乘法的一面：如果 n 和 m 是分别是两个可以被写成两个平方和的整数，那么它们的乘积nm 也同样可以。事实上，假设 $n = a^{2} + b^{2} ,m = c^{2} + d^{2}$ ，并考虑复数

$x + iy = (a + ib)(c + id)$ 。

很显然，x 和 y是两个整数，因为 a，b ，c，d∈ℤ ，通过对等式两边取绝对值(译注：取模再平方)，我们可以看到

$x^{2} + y^{2} = (a^{2 }+ b^2{})( c^{2 }+ d^{2})$ ，

这就可以推出 $nm = x^{2} + y^{2}$ 。

由于这三个原因，n 的可除(divisibility)属性在确定 $r_{2}(n)$ 的过程中起着关键作用。为了表述基本结论，我们定义两个新的除数函数(divisor functions):我们令 $d_{1}(n)$ 表示形如 4k + 1 的 n的除数数量，令 $d_{3}(n)$ 表示形如 4k + 3 的 n的除数数量。这一节的主要结论就是提供一个两个整数平方和问题的完整答案：

定理 3.1 若 n ≥ 1 ,则 $r_{2}(n) = 4(d_{1}(n) - d_{3}(n))$ 。

上述 $r_{2}(n)$ 的公式的一个直接结果可以表述如后。若 $n = p_{1}^{a_{1}}...p_{r}^{a_{r}}$ 是 n 的素因子分解，其中 $p_{1},...,p_{r}$ 各不相同，则：

当且仅当出现在 n 的因子分解中的形如 4k + 3 的每一个素数 $p_{j}$ 具有一个偶数指数 $a_{j}$ 的时候，正整数 n 才可以表示成两个整数的平方和。

练习 9 概述了这一推论的证明。

为了证明这一定理，我们首先建立一种将序列 $\{\{r_{2}(n)\}\}_{n=1}^{\infty}$ 的生成函数与θ函数的平方关联起来的关键关系，即

(6) $\displaystyle \theta^{2}(\tau)=\sum_{n=0}^{\infty}r_{2}(n)q^{n}$ ，

其中， $q=e^{{\pi}i\tau}$ 且 𝒯∈ℍ 。这个恒等式的证明仅取决于 $r_{2}$ 和的 θ 定义。事实上，若我们首先回顾 $\theta(\tau) = \sum_{-\infty}^{\infty}q^{n^{2}}$ ，则我们求得

$\begin{array}{rlc} \displaystyle \theta^{2}(\tau)=&\displaystyle\left (\sum_{n_{1}=-\infty}^{\infty}q^{n_{1}^{2}} \right )\left (\sum_{n_{2}=-\infty}^{\infty}q^{n_{2}^{2}} \right ) \\ \\ =&\displaystyle \sum_{(n_{1},n_{2})\in \mathbb{Z}\times \mathbb{Z}}{q^{n_{1}^{2}+n_{2}^{2}}} \\ \\ =&\displaystyle \sum_{n=0}^{\infty}r_{2}(n)q^{n} \end{array}$ ，

原因在于 $r_{2}(n)$ 计数了满足 $n_{1}^{2}+n_{2}^{2}=n$ 的数对 $(n_{1},n_{2})$ 的数量。

命题 3.2 只要 $q = e^{{\pi}i\tau}$ 且 𝒯∈ℍ，则就有恒等式 $r_{2}(n) = 4(d_{1}(n) - d_{3}(n))( n \ge 1)$ 等价于恒等式

(7) $\displaystyle \theta^{2}(\tau)=2\sum_{n=-\infty}^{\infty}\frac{1}{q^{n}+q^{-n}}=1+4\sum_{n=1}^{\infty}\frac{q^{n}}{1+q^{2n}}$ 。

证明：

我们首先注意到，由于 |q| < 1 ，则两个级数都是绝对收敛的，显然两个级数等价，因为 $1/(q^{n}+q^{-n}) = q^{|n|}/(1 + q^{2|n|})$ 。

由于 $(1 + q^{2n})^{-1} = (1 - q^{2n})/(1 - q^{4n})$ ，(7) 的右边等于

$\displaystyle 1+4\sum_{n=1}^{\infty}\left (\frac{q^{n}}{1-q^{4n}}-\frac{q^{3n}}{1-q^{4n}} \right )$ 。

然而，由于 $\displaystyle 1/(1 - q^{4n}) = \sum_{m=0}^{\infty}q^{4nm}$ ，我们有

$\displaystyle \sum_{n=1}^{\infty}\left (\frac{q^{n}}{1-q^{4n}} \right )=\sum_{n=1}^{\infty}\sum_{m=0}^{\infty}q^{n(4m+1)}=\sum_{k=1}^{\infty}d_{1}(k)q^{k}$ ，

因为 $d_{1}(k)$ 计数了形如 4m + 1 的k的除数的数量。注意到，级数 $\sum{d_{1}(k)q^{k}}$ 收敛，因为 $d_{1}(k) \leq k$ 。

类似的论证证明

$\displaystyle \sum_{n=1}^{\infty}\left (\frac{q^{3n}}{1-q^{4n}} \right )=\sum_{k=1}^{\infty}d_{3}(k)q^{k}$ ,

因此，命题证明完成。

事实上，我们发现，恒等式(6)将算术中的原始问题与建立关系(7)的复分析问题联系了起来。

现在我们将会发现用 𝒞(𝒯)来表示(7)更为方便(注：我们用符号 𝒞 来表示这个函数，因为我们正在对余弦级数(cosines)求和)：

(8) $\displaystyle \mathcal{C}(\tau)=2\sum_{n=-\infty}^{\infty}\frac{1}{q^{n}+q^{-n}}=2\sum_{n=-\infty}^{\infty}\frac{1}{\cos{n{\pi}}\tau}$ ，

其中， $q=e^{{\pi}i\tau}$ 且 𝒯∈ℍ 。然后，我们的工作就成了证明恒等式 $\theta^{2}(\tau) = \mathcal{C}(\tau)$ 。

真正值得注意的是函数 θ 和 𝒞 产生不同但并行的方式。函数θ的起源(genesis)可以被认为是实线上的热扩散方程(heat diffusion equation)；相应的热传导核根据 Gauss 函数 $e^{-{\pi}x^{2}}$ (其Fourier变换是其自身)给出；最后，θ 的变换法则导致了Poisson 求和公式的出现。

𝒞 的并行表示由另一个微分方程产生：带域中的稳态热传导方程；在那里，相应的核是 $1/\cosh{{\pi}x}$ (第 8 章 1.3 节)，这又是它自己的Fourier变换(第 3 章示例 3)。 𝒞 的变换规则再次来自Poisson求和公式。

为了证明恒等式 $\theta^{2}=\mathcal{C}$ ，我们将首先证明这两个函数满足同一个结构属性。对于 $\theta^{2}$ ，我们有变换律 $\theta^{2}(\tau) = (i/\tau)\theta^{2}(-1/\tau)$ (推论1.7)。

对于𝒞(𝒯)而方，同样的变换律也成立！事实上，如果我们在第4 章关系式(5)中设 a = 0 我们求得

$\displaystyle \sum_{n=-\infty}^{\infty}\frac{1}{\cosh({\pi}nt)} = \frac{1}{t}\sum_{n=-\infty}^{\infty}\frac{1}{\cosh({\pi}n/t)}$ 。

这恰好是恒等式

𝒞(𝒯) = (i/𝒯)𝒞(-1/𝒯) 。

对于 𝒯 = it (t > 0) ，根据解析延拓，这对于所有 𝒯∈ℍ 也成立。

从二者的定义出发，很显然，当 Im(𝒯) ⟶ ∞ 时， $\theta^{2}(\tau)$ 和 𝒞(𝒯) 均趋近于 1 。我们想验证的最后一个属性是两个函数在“尖点(cusp)” 𝒯 = 1 处的行为(注：为什么我们称点 𝒯 = 1 为尖点，以及其重要性的原因，稍后会变得更加清晰)。

对于 $\theta^{2}$ ,我们援引推论1.8可看到，当 Im(𝒯) ⟶ ∞ 时， $\theta^{2}(1-1/\tau) \sim 4(\tau/i) e^{\tau{i}\tau/2}$ 。

对于 𝒞 ，我们可以做同样的验证，再次利用 Poisson求和公式。事实上，若我们在第4 章关系式(5)中设 a = 0 我们求得

$\displaystyle \sum_{n=-\infty}^{\infty}\frac{(-1)^{n}}{\cosh({\pi}n/t)} = t\sum_{n=-\infty}^{\infty}\frac{1}{\cosh({\pi}(n+1/2)/t)}$ 。

因此，根据解析延拓我们推导出

$\displaystyle (1-1/\tau)= (\frac{\tau}{i})\sum_{n=-\infty}^{\infty}\frac{1}{\cosh({\pi}(n+1/2)/t)}$ 。

这个和的主要项是 n = -1 和 n = 0 的那些项。这很容易就给出

$\displaystyle (1 - 1/\tau) = 4(\frac{\tau}{i}) e^{{\pi}i\tau/2} + O(|\tau|e^{-3{\pi}t/2})$ (当 t ⟶ ∞ 时)，

其中，𝒯 = σ + it 。我们以一个命题来总结我们的结论。

命题 3.3 定义于上半平面的函数 $\mathcal{C}(\tau) = 1/\cos{n{\pi}\tau}$ 满足下述条款：

(i) 𝒞(𝒯 + 2) = 𝒞(𝒯) ；

(ii) 𝒞(𝒯) = (i/ 𝒯)𝒞(-1/𝒯)；

(iii) 当 Im(𝒯) ⟶ ∞ 时 𝒞(𝒯) ⟶ 1；

(iv) 当 Im(𝒯) ⟶ ∞ 时 $\mathcal{C}(1 - 1/\tau) \sim 4(\tau/i) e^{{\pi}i\tau/2}$ ；

此外， $\theta^{2}$ 同样满足上述条款。

有了这个命题，并在下列定理的辅助下我们证明恒等式 $\theta^{2}(\tau)=\mathcal{C}(\tau)$ ，其中，我们最终会设 $f = \mathcal{C}/{\theta}^{2}$ 。

定理 3.4 假设 f 是上半平面中的一个全纯函数，并满足以下条款：

(i) f (𝒯 + 2) = 𝒞(𝒯) ,

(ii) f (-1/𝒯) = f (𝒯),

(ii) f 有界，

则 f 是常量。

对于这个定理的证明，我们引入如下形式的闭合上半平面的子集，其定义为

$\mathcal{F} = \{ \tau \in \overline{H} : |\mathrm{Re}(\tau)| \le 1\: \mathrm{and}\: |\tau| \ge 1 \}$ ，

如下图 1 所示。

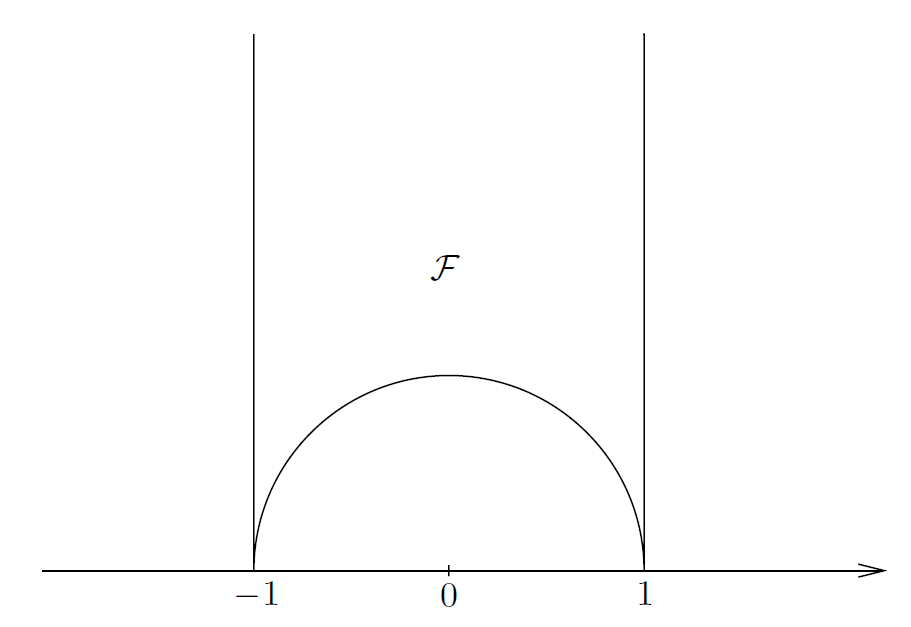
----------------------------------------------------------图 1： ℱ 域 -----------------------------------------------------

对应 𝒯 = ±1 的点称为尖点。在映射 𝒯 ⟼ 𝒯 + 2 下它们是等价的。

引理 3.5 在上半平面中的每个点都被反复使用下列一个或另一个分数线性变换或其逆变换映射到 ℱ：

$T_{2} : \tau \mapsto \tau + 2 , S: \tau \mapsto -1/\tau$ 。

由于这个原因，ℱ 被称为由于 $T_{2}$ 和 S 生成的变换群的基础域(fundamental domain)。

事实上，我可以令 G 为由于 $T_{2}$ 和 S 生成的变换群。由于 $T_{2}$ 和 S 是分数线性变换，若我们取 $\displaystyle g(\tau) = \frac{a\tau+b}{c\tau+d}$ ，则我们可以使用矩阵

$g=\begin{pmatrix} a&b\\ c&d \end{pmatrix}$

来表示每一个元素 g∈G 。由于表示 $T_{2}$ 和 S 的矩阵具有整数系数和行列式 1 ,则 G 中的所有元素矩阵也如此。特别是，若 𝒯∈ℍ ，则

(9) $\displaystyle \mathrm{Im}(g(\tau)) = \frac{\mathrm{Im}(\tau)}{|c\tau+d|^{2}}$ 。

引理3.5 的证明：

令 𝒯∈ℍ 。若 g∈G 且 g(𝒯) = (a𝒯 + b)/(c𝒯 + d) ，则 c和d 是整数，根据 (9) ，我们可以选择一个 $g_{0}\in G$ 使得 $\mathrm{Im}(g_{0}(\tau))$ 极大化。由于平移 $T_{2}$ 和其逆并没有改变虚部，我们可以应用有限多次平移以看到，存在 $g_{1} \in G$ 且 $|\mathrm{Re}(g_{1}(\tau))| \le 1$ 且 $\mathrm{Im}(g_{1}(\tau))$ 具有极大化。现在，只需证明 $|g_{1}(\tau)| \ge 1$ 从而推断出 $g_{1}(\tau) \in \mathcal{F}$ 即可。如果这不成立，即 $|g_{1}(\tau)| < 1$ ，则 $\mathrm{Im}(Sg_{1}(\tau))$ 会大于 $\mathrm{Im}(g_{1}(\tau))$ ，因为

$\displaystyle \mathrm{Im}(Sg_{1}(\tau)) = \mathrm{Im}(-1/g_{1}(\tau)) =-\frac{\mathrm{Im}(\overline{g_{1}(\tau)})}{|g_{1}(\tau)|^{2}}>\mathrm{Im}(g_{1}(\tau))$ ，

这与 $\mathrm{Im}(g_{1}(\tau))$ 的极大化(maximality)矛盾。

现在，我们可以证明这个定理了。假设 f 不是常量。令 g(z) = f ( 𝒯 )（ $z = e^{{\pi}i\tau}$ ）。z的函数 g在穿孔单位圆盘上是定义明确的，因为 f 是以 2 为周期的周期函数，此外，根据定理的假设(iii), g在原点附近有界。因此，0 是g 的一个可除奇点，且 $\displaystyle \lim_{z \rightarrow 0}g(z)=\lim_{\mathrm{Im}(\tau)\rightarrow \infty}f(\tau)$ 存在。因此，根据最大模原理，

$\displaystyle \lim_{\mathrm{Im}(\tau)\rightarrow \infty}|f(\tau)| < \sup_{\tau\in \mathcal{F}}|f(\tau)|$ 。

现在，我们必须考察 f 在点 ±𝒯 处的行为。由于 f ( 𝒯 + 2) = f ( 𝒯 ) ，则只需考虑 𝒯 = 1 即可。我们断言(claim)

$\displaystyle \lim_{\mathrm{Im}(\tau)\rightarrow \infty}f(1-1/\tau)$

存在，此外

$\displaystyle \lim_{\mathrm{Im}(\tau)\rightarrow \infty}|f(1-1/\tau)| < \sup_{\tau\in \mathcal{F}}|f(\tau)|$ 。

这个论证与上述论证基本上是相同的，不同之处在于我们首先必须交换 𝒯 = 1 与无穷远处的点。换句话说，我们希望考察当 𝒯 位于 ∞ 附近时函数 F(𝒯) = f (1 – 1/𝒯 ) 的行为。重要的一步在于证明 F 是周期函数。为此目的，我们考虑与矩阵

$U_{n}=\begin{pmatrix} 1-n&n \\ -n&1+n \end{pmatrix}$

3.2 四整数平方定理(The four-squares theorem)

定理的表述

在本章的其余部分，我们将考虑四个整数平方的情况。更准确地说，我们将证明每个正整数都是四个整数的平方和，此外，我们将确定 $r_{4}(n)$ 的公式，该公式描述了实现此目的的多种方法。

我们需要引入另外的除法函数，我们用 $\sigma_{1}^{*}$ 表示，它等于不能被4整除的 n 的除数的和。我们将证明的主要定理如下。

定理 3.6 每一个正整数都是四个整数的平方平，此外，

$r_{4}(n) = 8\sigma_1^{*}(n)$ (对于所有 n ≥ 1)。

如前一样，我们将序列 $\{ r_{4}(n) \}$ 通过其生成函数与θ 函数的一个合适的幂关联起来，在这个案例中这个合适的幂是其 4 次幂。结果是

$\displaystyle \theta^{4}(\tau) = \sum_{n=0}^{\infty}r_{4}(n)q^{n}$ (其中， $q = e^{{\pi}i\tau }$ 且 𝒯∈ℍ ) 。

下一步是求得其与 $\theta^{4}(\tau)$ 的等式表达了恒等式 $r_{4}(n) = 8\sigma_{1}^{*}(n)$ 。遗憾的是，这里没有什么比二整数平方和定理中出现的函数 𝒞(𝒯) 更简单的了。相反，我们需要构建上一章中考虑的Eisenstein级数的一个相当微妙的变体。事实上，对于 𝒯∈ℍ ，我们定义

$\displaystyle E_{2}^{*}(\tau)=\sum_{m}\sum_{n}\frac{1}{(\frac{m\tau}{2}+n)^{2}}-\sum_{m}\sum_{n}\frac{1}{(m\tau+\frac{n}{2})^{2}}$ 。

指定的求和顺序至关重要，因为上述级数并不绝对收敛。下面将四整数平方和定理简化为 $E_{2}^{*}$ 的模属性。

命题 3.7 论断 $r_{4}(n) = 8\sigma_{1}^{*}(n)$

$\displaystyle \theta^{4}(\tau) = \frac{-1}{{\pi}^{2}}E_{2}^{*}(\tau)$ (其中 𝒯∈ℍ ) 。

证明：

只需证明若 $q = e^{{\pi}i\tau}$ ，则

$\displaystyle \frac{-1}{{\pi}^{2}}E_{2}^{*}(\tau)= 1+\sum_{k=1}^{\infty}8\sigma_{1}^{*}(k)q^{k}$

即可。

首先，回想一下我们在上一章最后一节中讨论过的被禁用的Eisenstein级数，定义为

$\displaystyle F(\tau)=\sum_{m}\left [\sum_{n} {\frac{1}{(m\tau+n)^{2}}}\right ]$ ，

其中，n = m = 0 的项被忽略。由于以述和并非绝对收敛，因此求和次序非常关键，先 n 后m 。明白这点之后，由 $E_{2}^{*}$ 和 F 的定义立即可给出

(10) $\displaystyle E_{2}^{*}(\tau)=F(\frac{\tau}{2})-4F(2\tau)$ 。

在上一章的引理 2.6(和练习7)中，我们证明了

$\displaystyle F(\tau)=\frac{{\pi}^{2}}{3}-8{\pi}^{2}\sum_{k=1}^{\infty}\sigma_{1}(k)e^{2{\pi}ik\tau}$ ，

其中， $\sigma_{1}(k)$ 是 k 的除数之后。现在我们注意到

事实上，若 n 不能被4整除，没 4 没有除数被除4整除。若 $n = 4\widetilde{n}$ ，d 是可以被 4整除的 n 的一个除数，比如 $d=4\widetilde{d}$ ，则 $\widetilde{d}$ 整除 $\widetilde{n}$ 。这就给出了第二个公式。因此，基于个观察和(10)我们求得

$\displaystyle E_{2}^{*}(\tau)=-{\pi}^{2}-8{\pi}^{2}\sum_{k=1}^{\infty}\sigma_{1}^{*}(k)e^{{\pi}ik\tau}$ ，

因此，这个命题的证明完成。

因此，我们将定理 3.6 简化为恒等式 $\theta^{4}=-{\pi}^{-2}E_{2}^{*}$ ，建立这个关系的关键在于 $E_{2}^{*}$ 与 $\theta^{4}(\tau)$ 一样满足同样的模属性。

命题 3.8 定义在上半平面的函数 $E_{2}^{*}(\tau)$ 具有下列属性：

(i) $E_{2}^{*}(\tau+2)=E_{2}^{*}(\tau)$ ；

(ii) $E_{2}^{*}(\tau)=-\tau^{-2} E_{2}^{*}(-1/\tau)$ ；

(iii) 当 Im(𝒯)⟶ ∞时， $E_{2}^{*}(\tau) \rightarrow -{\pi}^{2}$ ；

(iv) 当Im(𝒯)⟶ ∞时， $E_{2}^{*}(1-1/\tau) =O(|\tau^{2}e^{{\pi}i\tau}|)$ 。

此外， $-{\pi}^{-2}\theta^{4}$ 具有以上同样的属性。

$E_{2}^{*}$ 的周期性 (i) 从函数的定义即可推出。 $E_{2}^{*}$ 的其它属性的证明稍涉及更多的一些东西。

考虑被禁止的Eisenstein级数 F 及其逆 $\widetilde{F}$ (将求和顺序颠倒后得到)：

$\displaystyle F(\tau)=\sum_{m}\sum_{n} {\frac{1}{(m\tau+n)^{2}}}$ 和 $\displaystyle \widetilde{F}=\sum_{n}\sum_{m} {\frac{1}{(m\tau+n)^{2}}}$ 。

在两种情况下，都忽略掉 m = n = 0 的项。

引理 3.9 函数 $F$ 和 $\widetilde{F}$ 满足：

(a) $F(-1/\tau ) = \tau^{2}\widetilde{F}(\tau)$ ，

(b) $F(\tau) -\widetilde{F}(\tau) = 2{\pi}i/\tau$ ，

证明：

属性(a)可直接从 $F$ 和 $\widetilde{F}$ 的定义和恒等式

$(n+m(-1/\tau))^{2} = \tau^{-2}(-m+n\tau)^{2}$

可推出。为了证明(b)，我们援引先前建立的Dedekind η 函数的函数方程：

$\displaystyle \eta(-1/\tau) = \sqrt{\frac{\tau}{i}}\eta(\tau)$ ，

其中， $\eta(\tau) = q^{\frac{1}{12}}\prod_{n=1}^{\infty}(1-q^{2n} )$ 且 $q = e^{{\pi}i\tau}$ 。

首先，我们针对变量 𝒯 取η 的对数导数以求得(根据第5章命题3.2)

$\displaystyle (\eta^{'}/\eta)(\tau) = \frac{{\pi}i}{12} - {2{\pi}i}{\sum_{n=1}^{\infty}}\frac{nq^{2n}}{1-q^{2n}}$ 。

然而，若用 $\sigma_{1}(k)$ 表示 k 的除数之和，则我们可以看到

$\begin{array}{rlc} \displaystyle \sum_{n=1}^{\infty}\frac{nq^{2n}}{1-q^{2n}}=&\displaystyle \sum_{n=1}^{\infty}\sum_{\ell=0}^{\infty}nq^{2n}q^{2{\ell}n} \\ \\ =&\displaystyle \sum_{n=1}^{\infty}\sum_{m=1}^{\infty}nq^{2nm} \\ \\ =&\displaystyle \sum_{k=1}^{\infty}\sigma_{1}(k)q^{2k} \end{array}$ 。

如果我们回顾 $\displaystyle F(\tau)=\frac{{\pi}^{2}}{3}-8{\pi}^{2}\sum_{k=1}^{\infty}\sigma_{1}(k)q^{2k}$ , 我们求得

$\displaystyle (\eta^{'}/\eta)( \tau ) = \frac{i}{4\pi}F(\tau)$ 。

根据链式法则，η (-1/𝒯 )的对数导数是 $\tau^{-2}(\eta^{'}/\eta)(-1/\tau)$ ，并使用属性(a)，我们看到 η(-1/𝒯 )的对数导数等于 $(i/4\pi)\widetilde{F}(\tau)$ 。因此，取η的函数方程的对数导数我们求得

$\displaystyle \frac{i}{4\pi}\widetilde{F}(\tau) = \frac{i}{2\tau}+\frac{i}{4\pi}F(\tau)$ ，

这就给出了 $\widetilde{F}{(\tau)} = -2{\pi}i /\tau + F(\tau)$ ，正如预期。

最后，(c) 是 (a) 和 (b) 的一个结果。

为了证明 $E_{2}^{*}$ 在 𝒯 ⟼ -1/𝒯 下的变换公式，我们从

$E_{2}^{*}(\tau) = F(\tau/2) - 4 F(2\tau)$

入手。则

$\begin{array}{rlc} E_{2}^{*}(-1/\tau)=&\displaystyle F(-1/(2\tau )) - 4F (-2/\tau ) \\ \\ =&\displaystyle \left [4{\tau}^{2}F(2\tau) - 4{\pi}i\tau \right ] - 4\left [(\tau/2)^{2 }F(\tau/2) - {\pi}i\tau \right ] \\ \\ =&\displaystyle 4{\tau}^{2}F(2{\tau}) - 4({\tau}^{2}/4)F({\tau}/2) \\ \\ =&\displaystyle -{\tau}^{2}(F({\tau}/2) - 4 F(2{\tau})) \\ \\ =&\displaystyle -\tau^{2}E_{2}^{*}(\tau) \end{array}$ ，

正如预期。为了证明第三个属性，我们回顾

$\displaystyle F(\tau)=\frac{{\pi}^{2}}{3}-8{\pi}^{2}\sum_{k=1}^{\infty}\sigma_{1}(k)e^{2{\pi}ik\tau}$ ，

其中，当 $\mathrm{Im}(\tau)\rightarrow \infty$ 时，和式趋近于 0 。则，若我们使用事实

$E_{2}^{*}(\tau) = F(\tau/2) - 4 F(2\tau)$ ，

我们推断出 $\mathrm{Im}(\tau)\rightarrow \infty$ 时， $E_{2}^{*}(\tau) \rightarrow -{\pi}^{2}$ 。

为了证明最后一个属性，我们从证明

(11) $\displaystyle E_{2}^{*}(1 - 1/{\tau}) = {\tau}^{2}\left [F \left (\frac{{\tau}-1}{2} \right ) -F \left (\frac{{\tau}}{2} \right ) \right ]$ 。

根据 F 的变换公式我们有

$\begin{array}{rlc} \displaystyle F(1/2 - 1/2\tau ) = &\displaystyle F \left (\frac{\tau-1}{2\tau} \right ) \\ \\ = &\displaystyle \left (\frac{2\tau}{\tau-1} \right )^{2}F\left ( \frac{2\tau}{1-\tau} \right ) -2{\pi}i\frac{2\tau}{1-\tau} \end{array}$ ,

和

$\begin{array}{rlc} \displaystyle F\left (\frac{2\tau}{1-\tau} \right ) = &\displaystyle F(-2+2/(1-\tau)) \\ \\ = &\displaystyle F(2/(1-\tau)) \\ \\ = &\displaystyle \left (\frac{1-\tau}{2} \right )^{2}F \left (\frac{1-\tau}{2} \right )-2{\pi}i\frac{\tau-1}{2} \end{array}$ 。

因此，

$\displaystyle F(1/2 - 1/2\tau ) = \tau^{2} F \left (\frac{\tau-1}{2} \right ) - 2{\pi}i\frac{2\tau}{1-\tau} - 2{\pi}i \left ( \frac{2\tau}{\tau-1}\right)^{2}\left (\frac{\tau-1}{2\tau} \right )$ 。

但 $F(2 - 2/\tau ) = F(-2/\tau ) = (\tau^{2}/4 ) F(\tau/2) - 2{\pi}i \tau/2$ ，因此

$\begin{array}{rlc} \displaystyle E_{2}^{*}(1 - 1/\tau) =&\displaystyle F(1/2 - 1/2\tau ) - 4 F(2 - 2/\tau ) \\ \\ =&\displaystyle \tau^{2} \left [F \left (\frac{\tau-1}{2} \right )-F \left (\frac{\tau}{2}\right )\right ] - 2{\pi}i \left (\frac{2{\tau}}{1-{\tau}}+\frac{2{\tau}^{2}}{{\tau}-1}\right ) + 4{\pi}i {\tau} \\ \\ =&\displaystyle \tau^{2} \left [F \left (\frac{\tau-1}{2} \right )-F \left (\frac{\tau}{2}\right )\right ] \end{array}$ 。

这证明了(11) 。则最后一个事实可从它以及事实

$\displaystyle F(\tau)=\frac{{\pi}^{2}}{3}-8{\pi}^{2}\sum_{k=1}^{\infty}\sigma_{1}(k)e^{2{\pi}ik\tau}$

推导出。因此，命题 3.8 得证。

现在，我们通过考虑商 $f(\tau) = E_{2}^{*}(\tau)/\theta^{4}(\tau)$ ,并应用定理 3.4 (和证明两个整数平方和定理一样)来推导四整数平方和定理的证明。回顾当 $\mathrm{Im}(\tau)\rightarrow \infty$ 时， $\theta^{4}(\tau) \longrightarrow 1$ 以及 $\theta^{4}(1-1/\tau) \sim 16\tau^{2} e^{{\pi}i\tau}$ 。结论是 f(𝒯) 是常量，根据命题 3.8 这个常量是 $-{\pi}^{2}$ 。这就完成了对四整数平方和定理的证明。