题意:
给 T 组数据,每组数据含有一个 n,让你求出
题解:
一看到题目,我们会比较倾向于这样的打表。
void initial()
{
sum[1]=1;
for (int i=2 ; i<N ; ++i)
{
for (int j=i ; j<N ; j+=i)
{
d[j]++;
sum[j]+=(d[j]+1)*(d[j]+1)*(d[j]+1);
}
}
}然而返回结果,却是一直的TLE,那么显然这样的打表,是行不通的。
我们要更换一下思路,既然这样打表行不通,那么O(n)的线性筛呢?
我们先单独看 只有素因子的数的因子数情况。
例如 4 那么答案是 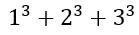
可以很容易发现,如果单独是一个素因子构成的数,分解成只有素因子组成的形式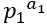
那么它的结果应该是
再扩展到含有其他素因子组成的数,即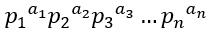
关键就在于,这样子是否成立。我们暂时忽略掉三次方。
实际上,这式子就是算出 当前被分解的这个数 N 的所有因子数的因子个数的和。
其实这式子,更像是单独求 N 的约数个数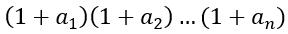
而题目要求的是要知道全部因子数的因子个数,所以给他们附上一定的权值 (自己觉得这里讲的有点牵强,可能需要自己理解一下)。
而根据组合来说,就可以很容易说明这式子的合法性。[实在觉得没办法理解合法性,自己手动写几个例如 12 啊 等等之类的合数,然后数学归纳法归纳一下。]
这个式子是成立的话,那么我们就可以用线性筛来打表了,因为我们 每次只需要知道最小素因子的个数,就可以打表了,跟约数个数是一个原理。证明我之前有一篇写线性筛的博客证明过,就不在这里证明了,有兴趣的可以自己找来看看 (OTL本渣渣写的还可能有错误呢,如果发现错误,麻烦帮忙指出来) 线性筛 [约数个数/约数和]
接下来还要处理三次方的问题。
先推荐这篇博客。有一个式子可以求出幂和的,即求
http://blog.miskcoo.com/2014/09/power-sum
有了这个式子,我们可以直接推导出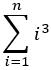
不想直接打表得到结果的,完全可以先筛全部素数,然后暴力分解 N,然后再用上面的式子得到答案。
====================================================================
这些小细节都知道怎么处理了,我们就可以开始打表了。
下面的各种情况,其实跟打约数个数跟约数和的情况是一直的,了解的话,完全可以自己知道式子就能打出来。因为之前写过一篇线性筛的博客,就懒得写的那么详细了。
sum[i]就是 i 的结果
num[i]就是 i 的最小素因子的个数
① n 是素数
那么结果显然是就是 (1+8) 就是说只有自己本身跟 1 这两个因子数,而本身的因子个数为 2。
记录下最小素因子个数。
sum[i]=1+8;
num[i]=1;
② i % prim[j] != 0
因为前面 i 中不存在 prim[j] 这个素因子,但是 i*prim[j] 中存在 prim[j] 这个素因子。
因此结果应该是 sum[i*prim[j]] = sum[i]*sum[prim[j]]
记录下当前最小素因子个数 num[i*prim[j]] = 1
(因为每次扫的必然是最小素因子,至于为什么,本身线性筛就是被最小素因子筛出来的)
③ i % prim[j] == 0
而这种情况,i 中包含了 prim[j] 这个素因子,意味着在最小素因子的那一项,会多了一项
即成了
原本的 i 应该是
那么为了得到 i*prim[j] 的结果
我们需要 将 sum[i] / 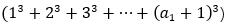
那么就需要用到我们之前记录下的最小素因子个数,来得到这个结果。
最后结果 sum[i*prim[j]] = sum[i] / s3(num[i]+1) * s3(num[i]+2) [s3 是用来求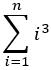
继续记录下最小素因子个数 num[i*prim[j]] = num[i] + 1
打表结束,我们就可以得到我们需要的答案了。
要说明一下,这个题的内存卡的有点严,如果再开一个数组就会 MLE 所以我没有直接再开一个数组来保存最小素因子那一项的和,而是直接用公式求出。
[OTL 再一次知道线性筛的厉害啊]
打表
#pragma comment(linker, "/STACK:102400000,102400000")
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<string>
#include<algorithm>
#include<queue>
#include<stack>
#include<set>
#include<map>
#include<vector>
using namespace std;
typedef long long ll;
const int N=5e6+5;
int prim[N],num[N],sum[N];
bool mark[N];
int cnt;
int s3(int x)
{
return (x+1)*(x+1)*(x+2)*(x+2)/4;
}
void initial()
{
cnt=0;
sum[1]=1;
for (int i=2 ; i<N ; ++i)
{
if (!mark[i])
{
prim[cnt++]=i;
num[i]=1;
sum[i]=9;
}
for (int j=0 ; j<cnt && i*prim[j]<N ; ++j)
{
mark[i*prim[j]]=1;
if (!(i%prim[j]))
{
num[i*prim[j]]=num[i]+1;
sum[i*prim[j]]=sum[i]/s3(num[i])*s3(num[i*prim[j]]);
break;
}
sum[i*prim[j]]=sum[i]*sum[prim[j]];
num[i*prim[j]]=1;
}
}
}
int main()
{
initial();
int T;
scanf("%d",&T);
while (T--)
{
int n;
scanf("%d",&n);
printf("%d\n",sum[n]);
}
return 0;
}暴力分解
#pragma comment(linker, "/STACK:102400000,102400000")
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<string>
#include<algorithm>
#include<queue>
#include<stack>
#include<set>
#include<map>
#include<vector>
using namespace std;
typedef long long ll;
const int N=1e4+5;
bool mark[N];
int prim[N];
int num[N];
int cnt;
void initial()
{
cnt=0;
for (int i=2 ; i<N ; ++i)
{
if (!mark[i])
prim[cnt++]=i;
for (int j=0 ; j<cnt && i*prim[j]<N ; ++j)
{
mark[i*prim[j]]=1;
if (!(i%prim[j]))
break;
}
}
}
ll divi(int n)
{
int k=0;
ll ans=1;
for (int i=0 ; i<cnt ; ++i)
{
if (prim[i]*prim[i]>n)
break;
if (!(n%prim[i]))
{
int ch=0;
while (!(n%prim[i]))
{
ch++;
n/=prim[i];
}
ans*=(ch+1)*(ch+1)*(ch+2)*(ch+2)/4;
}
}
if (n>1)
ans*=(1+8);
return ans;
}
int main()
{
initial();
int T;
scanf("%d",&T);
while (T--)
{
int n;
scanf("%d",&n);
printf("%lld\n",divi(n));
}
return 0;
}






 本文介绍了解决POJ-3604问题的方法,该问题要求计算给定整数的因子个数的立方和。文章首先尝试了朴素的打表方法并遇到TLE问题,随后通过线性筛法优化了算法,同时提供了暴力分解的解决方案。
本文介绍了解决POJ-3604问题的方法,该问题要求计算给定整数的因子个数的立方和。文章首先尝试了朴素的打表方法并遇到TLE问题,随后通过线性筛法优化了算法,同时提供了暴力分解的解决方案。




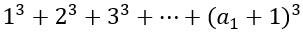
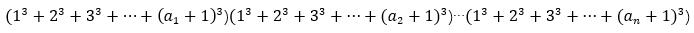
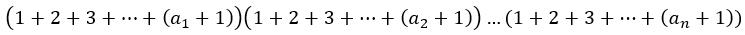
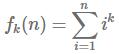
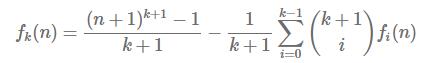
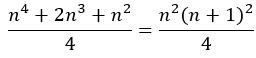
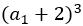
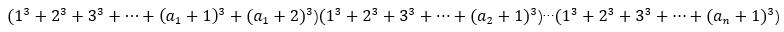
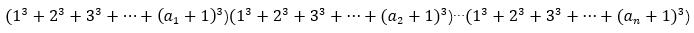
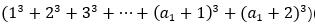
















 1215
1215

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








