计算机算法设计与分析第三章思维导图&&知识点总结

复习链接

计算机算法设计与分析第一章思维导图
计算机算法设计与分析第二章思维导图&&知识点总结
计算机算法设计与分析第三章思维导图&&知识点总结
计算机算法设计与分析第四章思维导图&&知识点总结
计算机算法设计与分析第五章思维导图&&知识点总结 ( 初稿 )
计算机算法设计与分析第六章思维导图&&知识点总结 ( 初稿 )
计算机算法设计与分析第七章思维导图&&知识点总结 ( 初稿 )

思维导图

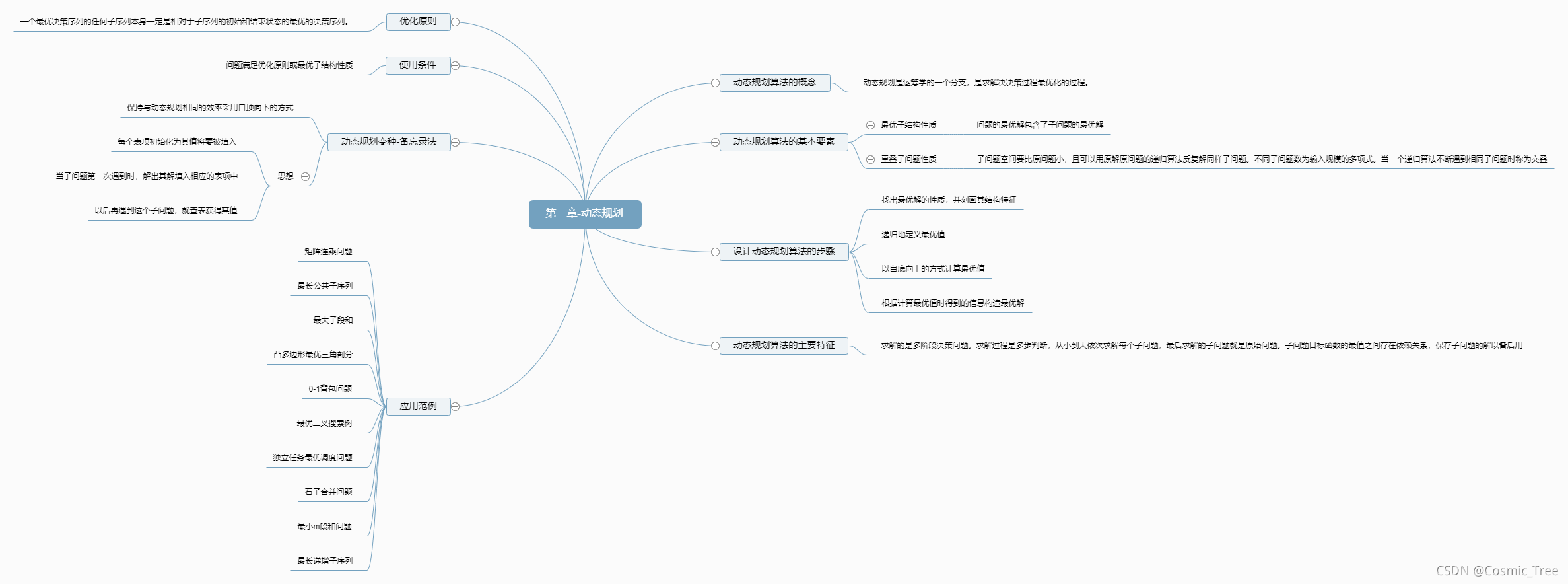
( 注：对应用范例，本文最后一部分给出了部分解释与分析 )

动态规划算法的概念

动态规划是运筹学的一个分支，是求解决决策过程最优化的过程。
动态规划算法与分治法类似，其基本思想是将待求解问题分解成若干子问题，先求解子问题，再结合这些子问题的解得到原问题的解。与分治法不同的是，适合用动态规划法求解的问题经分解得到的子问题往往不是互相独立的。若用分治法来解决这类问题，则分解得到的子问题数目太多，以致最后解决原问题需要耗费指数级时间。

动态规划算法的基本要素

（1）最优子结构性质

问题的最优解包含了子问题的最优解

（2）重叠子问题性质

子问题空间要比原问题小，且可以用原解原问题的递归算法反复解同样子问题。不同子问题数为输入规模的多项式。当一个递归算法不断遇到相同子问题时称为交叠

设计动态规划算法的步骤

（1）找出最优解的性质，并刻画其结构特征
（2）递归地定义最优值
（3）以自底向上的方式计算最优值
（4）根据计算最优值时得到的信息构造最优解

动态规划算法的主要特征

求解的是多阶段决策问题。求解过程是多步判断，从小到大依次求解每个子问题，最后求解的子问题就是原始问题。子问题目标函数的最值之间存在依赖关系，保存子问题的解以备后用

优化原则

一个最优决策序列的任何子序列本身一定是相对于子序列的初始和结束状态的最优的决策序列。

使用条件

问题满足优化原则或最优子结构性质，这是使用动态规划技术的必要条件

备忘录法

一个动态规划变种
保持与动态规划相同的效率
采用自顶向下的方式
思想：
每个表项初始化为其值将要被填入
当子问题第一次遇到时，解出其解填入相应的表项中
以后再遇到这个子问题，就查表获得其值

应用范例

矩阵连乘问题

状态转移方程：

$m[i][j]=\{\begin{array}{ll}0，& i=j\\ mi{n}_{i<=k<j}(m[i][k]+m[k+1][j]+p_{i-1}{p}_k{p}_j)，& i<j\end{array}$

物理意义：

$m[i][j]表示计算矩阵A[i:j]所需的最小数乘次数。$

最长公共子序列

状态转移方程：

$m[i][j]=\{\begin{array}{ll}0，& i>0;j=0\\ m[i-1][j-1]+1，& i,j>0;x_i=y_j\\ max(m[i][j-1],m[i-1][j])，& i,j>0;x_i\ne y_j\end{array}$

物理意义：

$m[i][j]记录序列X前i位和序列Y前j位的最长公共子序列的长度。$

最大子段和

状态转移方程：

$dp[j]=max(dp[j-1]+a[j],a[j])(1<=j<=n)$

物理意义：

$dp[j]表示前j个数中最大的连续字段和$

凸多边形最优三角剖分

状态转移方程：

$m[i][j]=\{\begin{array}{ll}0，& i=j\\ mi{n}_{i<=k<=j}(m[i][k]+m[k+1][j]+w(v_{i-1}{v}_k{v}_j))，& i<j\end{array}$

物理意义：

$m[i][j](1<=i<j<=n)$ $为凸子多边形$ $(v_{i-1},v_i,...,v_j)$ $的最优三角剖分对应的最优值$

0-1背包问题

状态转移方程：

$dp[i][j]=\{\begin{array}{ll}dp[i-1][j]，& j<w[i]\\ max(dp[i-1][j],dp[i-1][j-w[i]]+v[i])，& j>=w[i]\end{array}$

物理意义：

$dp[i][j]表示前i个物品容量为j时的最大价值$

优化：

$通过顺序枚举物品i，倒序更新j,可以优化掉第一层，只需记录一个容量j时的最大价值。空间复杂度由O（mn）变为O（m）。$

状态转移方程：

$dp[j]=max(dp[j],dp[j-w[i]]+v[i])$

物理意义：

$dp[j]表示物品容量为j时的最大价值$

最优二叉搜索树

状态转移方程：

$m[i][j]=\{\begin{array}{ll}0& 1<=i<=n;j=i-1\\ w_{i,j}+mi{n}_{i<=k<=j}(m[i][k-1],m[k+1][j])& 1<=i<=n,i<=j;\end{array}$

物理意义：

$m[i][j]表示包含点x_i,...,x_j的最优二叉查找树的期望代价。$

独立任务最优调度问题

思路：
m[i][j]表示前i个作业，在A上执行的时间为j时，在B上执行的最小时间。
对于第i个作业：
若j<a[i],则说明第i个作业是在B上执行的，因为若是在A上执行的j至少大于a[i],因此此时m[i][j]=m[i-1][j]+b[i]，表示前i-1个作业A上执行了j时间时的B执行时间加上第i个作业的时间。
若j>=a[i]，则m[i][j]=min(m[i-1][j]+b[i],dp[i-1][j-a[i]])。表示从第i个任务从B上执行与在A上执行的两个情况中取最小值。取最小值是因为，在A上的时间为固定的j情况下，那么我们B的时间，也就m的值，越小越好。
状态转移方程：

$m[i][j]=\{\begin{array}{ll}m[i-1][j]+b[i]& i<=n;0<=j<a[i]\\ min(m[i-1][j]+b[i],m[i-1][j-a[i]])& i<=n,a[i]<=j<=sum[i];\end{array}$

物理意义：

$m[i][j]表示前i个作业，在A上执行的时间为j时，在B上执行的最小时间。$
$sum[i]是指前i个作业在A上的时间和。$

石子合并问题

思路：
由于这是个圆形，我们考虑从n处截开，同时将产生的序列扩大一倍，形成
a[1],…,a[n],a[n+1]=a[1],…,a[n+n]=a[n],这样一个序列。
以最大值为例，设m[i][j]为合并区间i到j的最大代价。那么最终答案就是从m[i][i+n-1(1<=i<=n)中取最大值。
对于m[i][j]的求解，可以通过枚举分割点k(i<=k<j)来更新求值。

状态转移方程：

$m[i][j]=\{\begin{array}{ll}0& i=j\\ mi{n}_{i<=k<j}(m[i][k]+m[k+1][j]+sum(i,j))& i<j\end{array}$

$m[i][j]=\{\begin{array}{ll}0& i=j\\ ma{x}_{i<=k<j}(m[i][k]+m[k+1][j]+sum(i,j))& i<j\end{array}$

物理意义：

$m[i][j]为合并区间i到j的最大(最小)代价。$

最小m段和问题

思路：
m[i][j]记录长度为i，分j段后其子序列和的最大值的最小值。那么它由两部分构成：
当j=1时，m[i][1]表示的是长为i的整个序列的和；
当j>1时，m[i][j]=min(max(m[k][j-1], m[i][1]-m[k][1])(1<=k<=i));
这当中k表示的是分段的最后一段子序列的开始下标，所以m[k][j-1]是前面j-1段子序列和的最大值的最小值，m[i][1]-m[k][1]是最后一段子序列的和。所以取这两段中的最大值，在k值变化过程中取得到的最小值就是m[i][j]的答案。

状态转移方程：

$m[i][j]=\{\begin{array}{ll}m[i-1][j]+a[i]& i<=n;j=1\\ min(ma{x}_{1<=k<=i}(m[k][j-1],m[i][1]-m[k][1]))& i<=n,j>1\end{array}$

物理意义：

$用m[i][j]存储长度为i，分j段后其子序列和的最大值的最小值。$

最长递增子序列

状态转移方程：

$dp[i]=\{\begin{array}{ll}1，& i=j\\ max(dp[i],dp[j]+1)，& j<i且s[i]>s[j]\end{array}$

物理意义：

$dp[i]表示字符串前i位的最长递增子序列的长度$

优化：
顺序遍历字符串s，dp数组记录递增子序列，若当前字符比dp数组最大的还大，就将当前字符加入数组中，否则，就在dp数组中找一个x，满足x大于等于当前字符，用当前字符替换x。查找过程二分实现。遍历结束，dp数组的长度就是最长递增子序列的长度。
时间复杂度由O（n^2）优化到O（nlogn）