算法基础课-动态规划

动态规划

闫式dp法

• 状态表示：$dp(i,j,k,\dots )$
  • 变量组$(i,j,k,\dots )$表示的是什么集合
  • dp函数$dp(i,j,k...)$表示的是该集合的什么属性,即整个映射关系是$集合S⟶(i,j,k...)⟶\mathbb{R}$
• 状态计算：为了方便用状态转移进行计算，考虑的是集合的划分

但是也没有每一道题都可以硬套，只能说动态规划的题都很灵活

---

背包问题

最基本的模型，可以参考著名博客背包九讲

---

01背包

• 状态表示$dp(i,j)$：
  • $(i,j)$表示只从前i个物品中进行选择，且总体积小于等于（注意这里可能有所区别）j的选择方案
  • $dp(i,j)$表示所有选择里最大的价值
• 状态转移：将集合$(i,j)$划分为
  • 不选第i个物品：$集合(i-1,j)$只从前i-1个物品中进行选择，且总体积小于等于j的选择方案。
  • 必选第i个物品：$集合(i-1,j-v_i)\cup i$先只从前i-1个物品中进行选择，且总体积小于等于j-vi的选择方案，最后再加上i整个物品。
  • 状态转移方程$dp(i,j)=Max(dp(i-1,j),dp(i-1,j-v_i)+w_i)$

在具体代码中，还需要考虑初始化的问题

• $dp(0,\mathrm{0..}m)=0$是考虑如果一个都不选，那最大价值是0

#include <bits/stdc++.h>
using namespace std;

const int N = 1010;

int n,m;
int v[N],w[N];
int dp[N][N];

int main(){
	cin >> n >> m;
	for(int i = 1;i <= n;i++) cin >> v[i] >> w[i];
	
	//dp[0][0~m] = 0，但是静态变量自动是0
	for(int i = 1;i <=n ; i++){
		for(int j = 0;j <= m;j++){
			dp[i][j] = dp[i-1][j];//这是因为不选第i个物品的方案一定存在
			if(j >= v[i]) dp[i][j] = max(dp[i][j],dp[i-1][j-v[i]]+w[i]);//只有当前背包能放下第i个物品时，能用第i个物品进行更新
		}
	}
	
	cout << dp[n][m] << endl;
}

---

01背包的一维优化

这是注意到$dp[i][...]$只由$dp[i-1][...]$更新来，那i-1之前那么多数，存着也是没用。
那直接把这一维在空间中删去，我将其理解为“把第一维从空间的序列转化到时间的序列”

	for(int i = 1;i <=n ; i++){
		for(int j = 0;j <= m;j++){
			dp[j] = dp[j];//这是因为不选第i个物品的方案一定存在
			if(j >= v[i]) dp[j] = max(dp[j],dp[j-v[i]]+w[i]);//只有当前背包能放下第i个物品时，能用第i个物品进行更新
		}
	}

好像还能删点，dp[j] = dp[j]是废话，下面的if语句可以和for合并

	for(int i = 1;i <=n ; i++)//变成一个记录时间先后的维了
		for(int j = v[i];j <= m;j++)//直接从vi开始枚举体积
			dp[j] = max(dp[j],dp[j-v[i]]+w[i]);

现在检查一下，这样做对吗。很遗憾的是，把代码跑一遍，发现答案不对。我呢提出在哪？

我个人的理解是，滚动数组的思想是 用旧数据更新 新数据，新数据再覆盖旧数据

问题就出在，由于$j$从小到大进行枚举，所以在计算到$dp[j]$时，$dp[j-v[i]]$是已经被更新过的“新数据”。但我们想要的并不是用新数据来更新 .

所以解决方法也很简单，那就是要更新$dp[i][j]$时，让比$j$小的那些数还没被更新过就可以了，具体来说就是我们从大到小枚举$j$

	for(int i = 1;i <=n ; i++)//变成一个记录时间先后的维了
		for(int j = m;j >= v[i];j--)//从大到小枚举体积
			dp[j] = max(dp[j],dp[j-v[i]]+w[i]);

还有一种向一维进行优化的就是使用“滚动数组”，其实出发点是一样的，既然我们每次只是使用上一次的运算结果来更新这一次，那不妨就只开一个二维的数组$dp[2][m]$，其中一维部分是一个循环数组。

for(int i = 1;i <=n ; i++){
		for(int j = 0;j <= m;j++){
			dp[i%2][j] = dp[(i-1)%2][j];
			if(j >= v[i]) dp[i%2][j] = max(dp[i%2][j],dp[(i-1)%2][j-v[i]]+w[i]);
		}
	}
cout << dp[n%2][m] << endl;

同样的，这启发我们只要是递推时，第$i$次只跟 $i-k,i-k+1,...,i-1$次相关，就只需要开一个大小为$k+1$的循环数组

---

01背包不同的状态表示含义（不大于，恰等于，不少于）

直接查看博客

01背包 状态函数自变量因变量互换表示

• 正常表示中，$dp[j]$表示：(从前$i$个物品中选)体积为$j$能拿到的最大的价值
  • 状态转移：$dp[j]=Max(dp[j],dp[j-v_i]+w_i)$
  • 初始化：全负无穷，$dp[0]=0$
  • 最终答案：遍历所有$j\le 目标体积$，找到最大值
• 互换表示中，$dp[k]$表示：(从前$i$个物品中选)价值为$k$能拿到的最小的重量
  • 状态转移：$dp[k]=Min(dp[k],dp[k-w_i]+v_i)$
  • 初始化：全正无穷，$dp[0]=0$
  • 最终答案：从可能的最大的价值开始遍历$k$，直到找到第一个$dp[k]\le 目标体积$成立的值
• 用处：根据题目的范围$(N,V,W)$分别是数量、体积范围，价值范围。正常表示时空复杂度$O(NV)$，互换表示$O(NW)$，当$V$远大于$W$时，要选用互换表示

01背包：多维重量

基本上没有任何差别

• 状态表示$dp[j^1][j^2][...]$表示各维重量限制下，最大的价值
• 状态转移$dp[j^1][j^2][...]=Max(dp[j^1][j^2][...],dp[j^1-v_i^1][j^2-v_i^2][...]+w_i)$

完全背包

• 状态表示$dp(i,j)$：
  • $(i,j)$表示只从前i个物品中进行选择，且总体积小于等于j的选择方案
  • $dp(i,j)$表示所有选择里最大的价值
• 状态转移：将集合$(i,j)$划分为
  • 第i个物品选了k个，$k\in [0,\frac{j}{v_i}]$： 集合 ( i − 1 , j − k v i ) ∪ { k ∗ i } 集合(i-1,j-kv_i) \cup \{k*i\} 集合(i−1,j−kvi​)∪{k∗i}只从前i-1个物品中进行选择，且总体积小于等于j-k*vi的选择方案，再加上k个第i个物品。
  • 状态转移方程 d p ( i , j ) = M a x { d p ( i − 1 , j − k v i ) + k w i   ∣   k ∈ [ 0 , j v i ] } dp(i,j) = Max\{dp(i-1,j-kv_i)+kw_i \ | \ k \in [0,\frac{j}{v_i}]\} dp(i,j)=Max{dp(i−1,j−kvi​)+kwi​ ∣ k∈[0,vi​j​]}

初始化同01背包

这是个朴素的做法，需要三重循环

#include <bits/stdc++.h>
using namespace std;

const int N = 1010;

int n,m;
int v[N],w[N];
int dp[N][N];

int main(){
	cin >> n >> m;
	for(int i = 1;i <= n;i++) cin >> v[i] >> w[i];
	
	//dp[0][0~m] = 0，但是静态变量自动是0
	for(int i = 1;i <=n ; i++)
		for(int j = 0;j <= m;j++)
			for(int k = 0;k*v[i]<j;k++)//枚举数量
				dp[i][j] = max(dp[i][j],dp[i-1][j-k*v[i]]+k*w[i]);

	cout << dp[n][m] << endl;
}

这个时间复杂度很大

---

完全背包优化

优化的思路是，有没有什么东西是我们重复计算了呢

注意下面的对比

d p ( i , j ) = M a x { d p ( i − 1 , j ) ,    M a x { d p ( i − 1 , j − k v i ) + ( k − 1 ) w i + w i   ∣   k ∈ [ 1 , j v i ] }   } dp(i,j) = Max\{dp(i-1,j), \ \ Max\{dp(i-1,j-kv_i)+(k-1)w_i+w_i \ | \ k \in [1,\frac{j}{v_i}]\} \ \} dp(i,j)=Max{dp(i−1,j),  Max{dp(i−1,j−kvi​)+(k−1)wi​+wi​ ∣ k∈[1,vi​j​]} }
d p ( i , j − v i ) =                            M a x { d p ( i − 1 , j − k ′ v i ) + ( k ′ − 1 ) w i          ∣   k ′ ∈ [ 1 , j v i ] } dp(i,j-v_i) = \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ Max\{dp(i-1,j-k^{'}v_i)+(k^{'}-1)w_i \ \ \ \ \ \ \ \ | \ k^{'} \in [1,\frac{j}{v_i}]\} dp(i,j−vi​)=                          Max{dp(i−1,j−k′vi​)+(k′−1)wi​        ∣ k′∈[1,vi​j​]}

直接观察对比，我们有

$dp(i,j)=Max(dp(i-1,j),dp(i,j-v_i)+w_i)$

这简直就和01背包一模一样了

#include <bits/stdc++.h>
using namespace std;

const int N = 1010;

int n,m;
int v[N],w[N];
int dp[N][N];

int main(){
	cin >> n >> m;
	for(int i = 1;i <= n;i++) cin >> v[i] >> w[i];
	
	//dp[0][0~m] = 0，但是静态变量自动是0
	for(int i = 1;i <=n ; i++){
		for(int j = 0;j <= m;j++){
			dp[i][j] = dp[i-1][j];
			if(j >= v[i]) dp[i][j] = max(dp[i][j],dp[i][j-v[i]]+w[i]);
		}
	}
	
	cout << dp[n][m] << endl;
}

同样的，我们可以继续把空间优化成1维，但是令人惊奇的是，完全背包的第$i$回合的更新用到的竟然都是第$i$回的数据
这意思就是说，这里总是用已被更新过的来继续进行更新别的，那我们就不用再反向循环了

	for(int i = 1;i <=n ; i++)//变成一个记录时间先后的维了
		for(int j = v[i];j <= m;j++)//从大到小枚举体积
			dp[j] = max(dp[j],dp[j-v[i]]+w[i]);

---

多重背包问题

• 状态表示$dp(i,j)$：
  • $(i,j)$表示只从前i个物品中进行选择，且总体积小于等于j的选择方案
  • $dp(i,j)$表示所有选择里最大的价值
• 状态转移：将集合$(i,j)$划分为
  • 第i个物品选了k个，$k\in [0,s_i]$： 集合 ( i − 1 , j − k v i ) ∪ { k ∗ i } 集合(i-1,j-kv_i) \cup \{k*i\} 集合(i−1,j−kvi​)∪{k∗i}只从前i-1个物品中进行选择，且总体积小于等于j-k*vi的选择方案，再加上k个第i个物品。
  • 状态转移方程 d p ( i , j ) = M a x { d p ( i − 1 , j − k v i ) + k w i   ∣   k ∈ [ 0 , s i ] } dp(i,j) = Max\{dp(i-1,j-kv_i)+kw_i \ | \ k \in [0,s_i]\} dp(i,j)=Max{dp(i−1,j−kvi​)+kwi​ ∣ k∈[0,si​]}

朴素版本的多重背包简直就和完全背包问题一模一样

#include <bits/stdc++.h>
using namespace std;

const int N = 1010;

int n,m;
int v[N],w[N],s[N];
int dp[N][N];

int main(){
	cin >> n >> m;
	for(int i = 1;i <= n;i++) cin >> v[i] >> w[i] >> s[i];
	
	//dp[0][0~m] = 0，但是静态变量自动是0
	for(int i = 1;i <=n ; i++)
		for(int j = 0;j <= m;j++)
			for(int k = 0;k <= s[i] && k*v[i]<j;k++)//枚举数量
				dp[i][j] = max(dp[i][j],dp[i-1][j-k*v[i]]+k*w[i]);
	
	cout << dp[n][m] << endl;
}

---

多重背包优化

一个朴素的想法是模仿完全背包问题进行优化

d p ( i , j )          = M a x {                   d p ( i − 1 , j ) ,                   M a x { d p ( i − 1 , j − k v i ) + ( k − 1 ) w i + w i   ∣   k ∈ [ 1 , s i ] }   } dp(i,j) \ \ \ \ \ \ \ \ = Max\{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ dp(i-1,j), \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ Max\{dp(i-1,j-kv_i)+(k-1)w_i+w_i \ | \ k \in [1,s_i]\} \ \} dp(i,j)        =Max{                 dp(i−1,j),                 Max{dp(i−1,j−kvi​)+(k−1)wi​+wi​ ∣ k∈[1,si​]} }
d p ( i , j − v i ) = M a x { d p ( i − 1 , j − ( s i + 1 ) v i ) + s i w ,    M a x { d p ( i − 1 , j − k ′ v i ) + ( k ′ − 1 ) w i          ∣   k ′ ∈ [ 1 , s i ] } dp(i,j-v_i) = Max\{dp(i-1,j-(s_i+1)v_i)+s_iw, \ \ Max\{dp(i-1,j-k^{'}v_i)+(k^{'}-1)w_i \ \ \ \ \ \ \ \ | \ k^{'} \in [1,s_i]\} dp(i,j−vi​)=Max{dp(i−1,j−(si​+1)vi​)+si​w,  Max{dp(i−1,j−k′vi​)+(k′−1)wi​        ∣ k′∈[1,si​]}

然后发现多出来一项，寄了

只能换一种方法：二进制优化。总而言之就是进行打包

具体来说就是把$s_i$个物品进行打包，每包的个数分别是 { 2 0 , 2 1 , … , 2 l , s i + 1 − 2 l + 1 } \{2^0,2^1,\dots,2^l,s_i+1-2^{l+1}\} {20,21,…,2l,si​+1−2l+1}
类似某个数的二进制表示，我们可以选择这些“打包”中的某些包，表示出$[0,s_i]$中的每一个整数
注意到这样的“包”都是要么选，要么不选的性质。这就把一个多重背包转化成一个01背包

关于算法的正确性证明：其实就是 { 2 0 , 2 1 , … , 2 l , s i + 1 − 2 l + 1 } \{2^0,2^1,\dots,2^l,s_i+1-2^{l+1}\} {20,21,…,2l,si​+1−2l+1}能不能表示出$[0,s_i]$中的每一个整数
这里我们要求$2^{l+1}-1<s_i\le 2^{l+2}-1$
由二进制数的性质，容易得 { 2 0 , 2 1 , … , 2 l } \{2^0,2^1,\dots,2^l\} {20,21,…,2l}一定能表示出$[0,2^{l+1}-1]$中所有整数
$\forall x\in (2^{l+1}-1,s_i],令c=s_i+1-2^{l+1}$显然我们有$0<c\le 2^{l+1}$则$x-c\in [0,2^{l+1}-1]$
这说明$x-c$是可表示的，进而$x$是可表示的，进而$[0,s_i]$都是可表示的

#include <bits/stdc++.h>
using namespace std;

const int N = 25000;//把多重背包搞成01背包，要算nlogk
const int M = 2010;

int n, m;
int v[N], w[N];
int dp[N];

int main() {
	cin >> n >> m;

	//拆分成01背包
	int cnt = 0;//拆分数量,也即拆分成01物品的数量
	for (int i = 1; i <= n; i++) {
		int vv, ww, s; //当前物品的，体积，价值，个数
		cin >> vv >> ww >> s;

		int k = 1;//打包容量
		while (k <= s) {
			cnt++;
			v[cnt] = vv * k;
			w[cnt] = ww * k;
			s -= k;
			k *= 2;
		}
		if (s > 0) {
			cnt++;
			v[cnt] = vv * s;
			w[cnt] = ww * k;
		}
	}

	//01背包
	for (int i = 1; i <= cnt; i++)
		for (int j = m; j >= v[i]; j--)
			dp[j] = max(dp[j], dp[j - v[i]] + w[i]);
	cout << dp[m] << endl;
}

---

分组背包问题

• 状态表示$dp(i,j)$：
  • $(i,j)$表示只从前i组物品中进行选择，且总体积小于等于j的选择方案
  • $dp(i,j)$表示所有选择里最大的价值
• 状态转移：将集合$(i,j)$划分为
  • 第i组中物品选了第k个，$k\in [0,s_i]$： 集合 ( i − 1 , j − k v i , k ) ∪ { i k } 集合(i-1,j-kv_{i,k}) \cup \{i_k\} 集合(i−1,j−kvi,k​)∪{ik​}只从前i-1组物品中进行选择，且总体积小于等于j-k*vik的选择方案，再加上第k个物品。
  • 状态转移方程 d p ( i , j ) = M a x { d p ( i − 1 , j − k v i , k ) + k w i , k   ∣   k ∈ [ 0 , s i ] } dp(i,j) = Max\{dp(i-1,j-kv_{i,k})+kw_{i,k}\ | \ k \in [0,s_i]\} dp(i,j)=Max{dp(i−1,j−kvi,k​)+kwi,k​ ∣ k∈[0,si​]}

朴素做法

#include<bits/stdc++.h>
using namespace std;

const int N=110;
int dp[N][N];  
int v[N][N],w[N][N],s[N];   
int n,m,k;

int main(){
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		cin>>s[i];
		for(int j=0;j<s[i];j++){
			cin>>v[i][j]>>w[i][j];
		}
	}
	
	for(int i=1;i<=n;i++){
		for(int j=0;j<=m;j++){
			dp[i][j]=dp[i-1][j];
			for(int k=0;k<s[i];k++){
				if(j>=v[i][k]) dp[i][j]=max(dp[i][j],dp[i-1][j-v[i][k]]+w[i][k]);  
			}
		}
	}
	cout<<dp[n][m]<<endl;
}

同样的，同01背包，用i-1次更新i次，反向循环优化成一维

for(int i=1;i<=n;i++)
		for(int j=m;j>=0;j--)
			for(int k=0;k<s[i];k++)
				if(j>=v[i][k]) dp[j]=max(dp[j],dp[j-v[i][k]]+w[i][k]);  
cout<<dp[m]<<endl;

---

混合背包

同时存在01，多重，完全背包

• 将01背包和多重背包都视作多重背包
• 只是状态转移时进行区分即可，状态表示保持不变

#include <bits/stdc++.h>
using namespace std;

const int N = 1001;

int f[N];

int n,m;

int main(){
    cin >> n >> m;
    for(int i = 0;i < n;i++){
        int v,w,s;
        cin >> v >> w >> s;
        if(s == -1) s = 1;
        
        //多重背包
        if(s == 0){
            for(int j = v;j <= m;j++){
                f[j] = max(f[j],f[j-v]+w);
            }
        }
        
        //将01背包也作为多重背包
        else{
            for(int k = 1;k <= s;k*=2){//打包的数量
                //打包后做01背包
                for(int j = m;j >= k*v;j--){
                    f[j] = max(f[j],f[j-k*v]+k*w);
                }
                s -= k;
            }
            if(s != 0){
                for(int j = m;j >= s*v;j--){
                    f[j] = max(f[j],f[j-s*v]+s*w);
                }
            }
        }
    }
    
    cout << f[m] << endl;
}

---

线性dp

dp递推具有一定线性顺序·

---

数字三角形

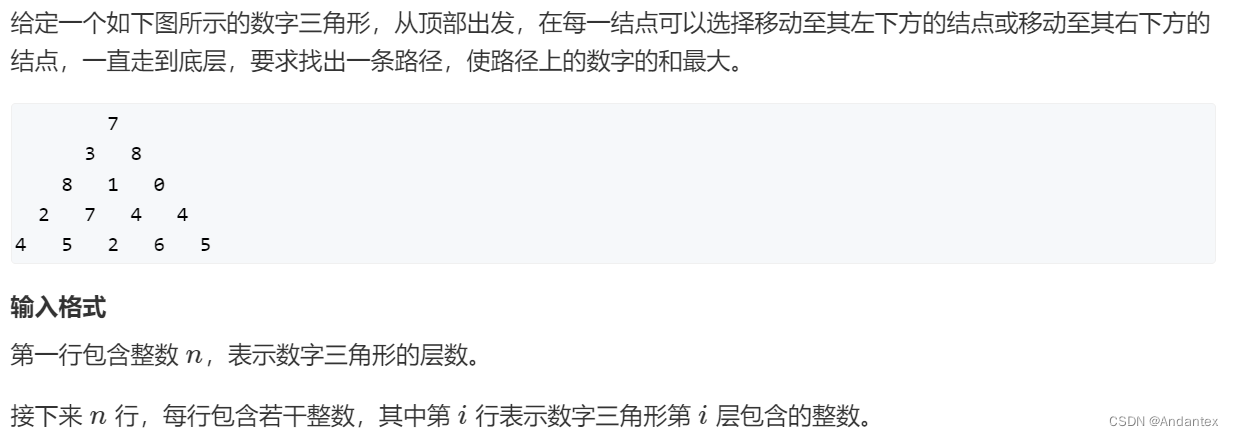
从上到下分别是1,2,3…行，每行从左到右分别是1,2,3,4,…列

• 状态表示$dp(i,j)$
  • 集合$(i,j)$：表示从$<1,1>$走到$<i,j>$的路径
  • 属性$dp(i,j)$:所有路径和的最大值
• 状态转移
  • 集合划分：$(i,j)=\{(i-1,j-1),<i,j>\}\cup \{(i-1,j),<i,j>\}$,就是从左上坐过来还是从右上走过来
  • 转移方程:$dp(i,j)=Max(dp(i-1,j-1),dp(i-1,j))+a[i,j]$

初始化：把所有状态初始化为负无穷（就是比任何数都小）
这是为了应对边界条件

#include <bits/stdc++.h>
using namespace std;

const int N = 510, INF = 1e9;

int n;
int a[N][N];
int f[N][N];

int main(){
	scanf("%d",&n);
	for(int i = 1;i <= n;i++)
		for(int j = 1; j <= i;j++)
			scanf("%d",&a[i][j]);
	
	//初始化
	for(int i = 0;i <= n;i++)
		for(int j = 0; j <= i+1;j++)
			f[i][j] = -INF;
	f[1][1] = a[1][1];
	
	for(int i = 2;i <= n;i++)
		for(int j = 1;j <= i;j++)
			f[i][j] = max(f[i-1][j-1],f[i-1][j])+a[i][j];
	
	int ans = -INF;
	//遍历最后一行
	for(int i = 1;i <= n;i++) ans = max(ans,f[n][i]);
	
	printf("%d\n",ans);
	return 0;
}

注：本题还有笼另外的方式，上面的做法是自顶向底，其实也可以自底向上，好处是最后不用遍历一遍求最大值了

---

最长上升子序列

• 状态表示$dp(i)$
  • 集合$(i)$：表示所有以第$i$个数结尾的上升子序列的集合
  • 属性$dp(i)$:所有子序列的最大长度
• 状态转移
  • 集合划分：$(i)=(0)\cup (1)...\cup (i-1)$,即按以i结尾的上升子序列中，倒数第二个数是谁进行划分。但是当且仅当$a_j<a_i$时，才存在
  • 转移方程: d p [ i ] = M a x { d p [ j ] + 1   ∣   a j < a i   ∧   0 ≤ j < i − 1 } dp[i] = Max\{dp[j]+1 \ | \ a_j<a_i \ \land \ 0 \leq j < i-1\} dp[i]=Max{dp[j]+1 ∣ aj​<ai​ ∧ 0≤j<i−1}

#include <bits/stdc++.h>
using namespace std;

const int N = 1010;

int n;
int a[N],f[N];

int main(){
	scanf("%d",&n);
	for(int i = 1;i <= n;i++) scanf("%d",&a[i]);
	
	for(int i = 1;i <= n;i++){
		f[i] = 1;//至少含有a[i]一个数
		for(int j = 1;j <= n;j++)
			if(a[j] < a[i]) f[i] = max(f[i],f[j]+1);
	}
	
	//遍历
	int res = 0;
	for(int i = 1;i <= n;i++) res = max(res,f[i]);
	printf("%d\n",res);
	return 0;
}

最长上升子序列的对偶问题 与 Dilworth 定理

定理

$$对于偏序集<A,\le >，设其中最长链长度为n，则若将A分解成不相交的反链，反链个数至少为n$$

说明：

• 链：偏序集的一个子集，使得在这个集合上偏序称为全序关系
• 反链：偏序集的一个子集，使得子集内任意两个元素不可比

证明：设反链的最小个数为$p$

• 首先$p\ge n$：这是因为由鸽巢原理，若$p\le n$，则一定存在某条反链，其内部含有最长链中的两个或以上的元素，这些元素是可比的，于是与反链定义矛盾
• 下证明$n\ge p$：进行构造性的证明
  • 记$A_1=A$，记$A_1$中所有极小元组成的集合是$X_1$，则$X_1$是一条反链（极小元之间不可能再可比）
  • 令$A_2=A_1-X_1$，则一定存在$a_1\in A_1,a_2\in A_2,s.t.a_1\le a_2$
  • 不断按照以上原则构造序列 { A i } , { X i } \{A_i\},\{X_i\} {Ai​},{Xi​}直到$A_k$为空，则按照以上讨论，我们得到$X_1,X_2,\dots ,X_k$是一个反链覆盖，同时得到一条链$a_1,a_2,\dots ,a_k$
  • $n$是最长链，$p$是反链覆盖最小大小，所以$n\ge k\ge p$,证毕

于是，在一个序列 { a i } \{a_i\} {ai​}取偏序关系是，序列中两个数，同时满足其中一个数的下标和值都大于另一个数，则这两个数存在一个关系。

于是，在该偏序关系下，链是序列的上升子序列，反链是下降子序列，于是根据该定理我们可以断言，最长上升子序列长度=最小下降子序列覆盖数

拓展：在动态规划中输出具体方案

方案的记录一般与状态转移这一步结合，具体来说就是记录一下每个新状态是由哪个旧状态转移来的

#include <bits/stdc++.h>
using namespace std;

const int N = 1010;

int n;
int a[N],f[N];
int g[N];

int main(){
	scanf("%d",&n);
	for(int i = 1;i <= n;i++) scanf("%d",&a[i]);
	
	for(int i = 1;i <= n;i++){
		f[i] = 1;
		for(int j = 1;j <= n;j++){
			if(a[j] < a[i]){
				if(f[j]+1 > f[i]){
					f[i] = f[j]+1;
					g[i] = j;//代表i状态由j状态转移来
				}
			}
		}
	}
	
	//遍历
	int length = 0,ending;
	for(int i = 1;i <= n;i++){
		if(f[i]>length){
			ending = i;
			length = f[i];
		}
	}
	
	stack<int> path;//逆序输出
	for(int i = 0,k = ending;i<length;i++,k = g[k]){//从尾部回溯
		path.push(k);
	}
	while(path.size()){
		printf("%d ",path.top());
		path.pop();
	}
	
	return 0;
}

---

最长上升子序列优化

更换状态表示，使得在状态转移时用二分，时间复杂度缩减为$O(nlogn)$

• 状态表示$dp(i)$
  • 集合$(i)$:所有长度为$i$的上升子序列
  • 属性$dp(i)$:所有当前子序列末尾数字的最小值
• 状态转移
  • 首先$dp(i)$是纯纯的单增函数
  • 为当前最长的子序列长度建立一个记录$cnt$
  • 如果当前$a_i>dp(cnt)$则$cnt++,dp(cnt)=a_i$
  • 如果小，则二分查找，找到满足$a_i\le dp(k)$的第一个下标$k$，更新$dp(k)=a_i$

#include <bits/stdc++.h>
using namespace std;

const int N = 1010;
int n, cnt;
int a[N], dp[N];

int main() {
	cin >> n;
	for (int i = 0 ; i < n; i++) cin >> a[i];
	
	dp[++cnt] = a[0];//dp[1]
	for (int i = 1; i < n; i++) {
		if (a[i] > dp[cnt]) dp[++cnt] = a[i];
		else {
			int l = 0, r = cnt - 1;
			while (l < r) {
				int mid = (l + r) >> 1;
				if (dp[mid] >= a[i]) r = mid;
				else l = mid + 1;
			}
			dp[r] = a[i];
		}
	}
	cout << cnt << endl;
	return 0;
}

---

最长公共子序列

• 状态表示$dp(i,j)$
  • 集合$(i,j)$：表示所有 同时在第一个集合的前i位和第二个集合的前k位出现的子序列
  • 属性$dp(i)$:所有子序列的最大长度
• 状态转移
  • 按是否有$a[i]==b[i]$进行划分
  • $a[i]==b[j]$：则可以直接加上该字母$dp(i-1,j-1)+1$
  • $a[i]\ne b[j]$：说明$a[i]$和$b[j]$不可能同时出现在最长公共子序列内。因此需要在下面两个数中选择最大值
    • $dp(i-1,j)$
    • $dp(i,j-1)$

#include<bits/stdc++.h>
using namespace std;

const int N = 1010;
int n, m;
char a[N], b[N];
int dp[N][N];
int main() {
	scanf("%d%d",&n,&m);
	scanf("%s%s",a+1,b+1);
	
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= m; j++) {
			if (a[i] == b[j]) {
				dp[i][j] = dp[i - 1][j - 1] + 1;
			} else {
				dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
			}
		}
	}
	
	printf("%d\n",dp[n][m]);
	return 0;
}

---

区间dp

通常该类题的状态表示的是区间的信息
$区间[i,j]⟶dp(i,j)$
整体的方法是枚举区间划分点

• 状态表示$dp(i,j)$，将第i堆石子到第j堆石子合并为一堆的最小代价
• 状态转移：把区间$[i,j]$劈开成为$[i,k]\cup [k+1,j]$，这是考虑在最后一步将左右两堆合并。所以 d p ( i , j ) = M i n { d p ( i , k ) + d p ( k + 1 , j ) + s u m ( i , j ) ∣ k ∈ [ i , j − 1 ] } dp(i,j) = Min\{dp(i,k)+dp(k+1,j)+sum(i,j)|k \in [i,j-1]\} dp(i,j)=Min{dp(i,k)+dp(k+1,j)+sum(i,j)∣k∈[i,j−1]}

本题有一点需要注意就是如何遍历所有状态，该顺序需要保证每次进行状态转移时用来进行状态转移的状态应该是已经被计算过的

注意到进行区间dp时，用来进行状态转移的区间都是比当前区间短的区间，所以枚举所有状态时应该按照长度从小到大进行枚举

#include<bits/stdc++.h>
using namespace std;

const int N = 310;

int n;
int s[N];//前缀和，快速查询总和
int dp[N][N];

int main(){
	scanf("%d",&n);
	for(int i = 1;i <= n;i++) scanf("%d",&s[i]);
	
	for(int i = 1;i <= n;i++) s[i] += s[i-1];//处理前缀和
	
	
	memset(dp,0x3f,sizeof dp);//初始化为无穷大
	for(int len = 1;len <= n;len++){//从小到大进行枚举区间长度
		for(int i = 1;i +len -1 <= n;i++){//枚举起点
			int l = i, r = i + len - 1;
			if(len == 1) dp[l][r] = 0;//边缘条件：一堆不需要合并
			else{
				for(int k = l;k < r;k++){//枚举分割点
					dp[l][r] = min(dp[l][r],dp[l][k]+dp[k+1][r]+s[r]-s[l-1]);
				}
			}
		}
	}
	
	printf("%d\n",dp[1][n]);
}

---

状态标识dp

这个标题名是我瞎起的，意思是这类dp问题中，用于标识状态的参数并不是那么显然了

状态机模型dp

此类问题一般能够使用一个类似于有限状态机的模型来表示整个事件，其组成元素包括

• 状态机
  • 节点：表示某个状态
  • 弧：表示状态转移的方向和条件
• 入口：即整个事件开始时，位于哪个状态
  • 用于 初始化
• 出口：即事件可能结束于哪个状态
  • 用于获得答案

在进行实现时，通常是在原有的状态数组上再开一维表示位于何状态的数组，其流程依旧是初始化->遍历->状态转移->查询答案，与常规动规的区别在于“状态转移”时需要按照状态机图来，见例子

例如：

• 给出状态机:

  • 入口是不持有股票
  • 出口也是不持有股票

• 给出状态表示：$现在是第i天，已经完成j次交易，不持有股票f(i,j,0)；持有股票f(i,j,1)$所达到的最大利润

• 给出状态转移

  • $f(i,j,0)=Max(f(i-1,j,0),f(i-1,j,1)+w_i)$
  • $f(i,j,1)=Max(f(i-1,j,1),f(i-1,j-1,0)-w_i)$

#include <bits/stdc++.h>
using namespace std;

const int N = 1e5+10,K=  110;


int f[N][K][2];

int n,k;

int main(){
    cin >> n >> k;
    
    memset(f,0xcf,sizeof f);//先假设全不合法
    for(int i = 0;i <= n;i++) f[i][0][0] = 0;//合法的结果初始化成0
    
    for(int i = 1;i <= n ;i++) {
        int w;
        cin >> w;
        for(int j = 1;j <= k;j++){
            f[i][j][0] = max(f[i - 1][j][0], f[i - 1][j][1] + w);
            f[i][j][1] = max(f[i - 1][j][1], f[i - 1][j - 1][0] - w);
        }
    }
    
    int ans = 0;
    for(int j = 0;j <= k;j++) ans = max(f[n][j][0],ans);
    
    cout << ans << endl;
    
}

---

状态压缩dp

我们有时候需要对状态进行记录，后面的“树上dp”也是对状态进行记录的例子
用状态函数的某一个参数记录了当前状态，通过压缩，一般是以二进制数的形式出现

例：

首先我们断定，假如所有横着的方片已经全放进去了，那竖着的放的方式是唯一的
所以只用考虑放横着的方片

• 状态表示$dp(i,j)$:

  • 集合$(i,j)$：只考虑前$i$列，在$j$表示的状态下，所有的放法
    • $j$表示的状态是哪些行上有终点在第$i$列的横向方片
      • 用二进制来表示状态，比如共有五行，倘若是第1行，第4行上有，则$j=(10010{)}_2=10$
  • $dp(i,j)$就表示放法的数量

• 状态转移：对于$dp(i,j)$，首先枚举所有可能的状态$j$，判断该状态能否由$dp(i-1,k)$转移

  • $j\&k=0$：表示两边没有冲突
  • $j|k$不存在连续奇数个0：在$i-1$这一列可以最终用竖着的方片放满
    

#include <bits/stdc++.h>
using namespace std;

const int N = 12,M = 1<<N;
int n,m;
long long int dp[N][M];
bool st[M];

int main(){
	int n,m;
	while(cin>>n>>m,n||m){
		memset(dp,0,sizeof dp);
		
		for(int i = 0;i < 1<<n;i++){//预处理出所有不含奇数连续0的状态
			st[i] = true;
			int cnt = 0;
			for(int j = 0;j < n;j++){
				if(i>>j & 1){//如果当前位是1
					if(cnt & 1) st[i] = false;//如果之前连续的0数量是奇数
					cnt = 0;
				}
				else cnt++;
			}
			if(cnt & 1) st[i] = false;
		}
		
		//0~m-1 列 是图片所在的位置
		dp[0][0] = 1;//不可能从-1列放横向方片，所以第二维是0，dp[0][0]代表什么都不干
		for(int i = 1;i <= m;i++){
			for(int j = 0;j < 1<<n;j++){
				for(int k = 0;k < 1<<n;k++){
					if((j&k)==0 && st[j|k]){
						dp[i][j] += dp[i-1][k];
					}
				}
			}
		}
		
		cout << dp[m][0] << endl;//输出dp[m][0]
	}
}

---

例：最短哈密尔顿路径

• 状态表示$dp(i,j)$:

  • 集合$(i,j)$：从$0$走到$j$，在$i$表示的状态下，所有的走法
    • $j$表示的状态是经过了哪些点了
      • 用二进制来表示状态，1表示经过了该点，0表示未经过该点
  • $dp(i,j)$就表示最短的路径

• 状态转移：按照是从那个点走到$j$来分类，遍历所有可能的k点, d p ( i − { j } , k ) + a k , j dp(i-\{j\},k)+a_{k,j} dp(i−{j},k)+ak,j​。意思是该状态只能从"从i走到k，且没有经过j这个点"的状态转移过来

#include <bits/stdc++.h>
using namespace std;

const int N = 20, M = 1 << N;

int n;
int w[N][N];
int dp[M][N];

int main(){
	cin>>n;
	for(int i = 0;i < n;i++)
		for(int j = 0;j < n;j++)
			cin >> w[i][j];
	
	memset(dp,0x3f,sizeof dp);
	
	dp[1][0] = 0;
	for(int i = 0;i < 1<<n;i++){
		for(int j = 0;j < n;j++){
			if(i>>j&1){//至少应该经过j这个点
				for(int k = 0;k < n;k++){//枚举上一个点
					if((i - (1<<j))>>k & 1){//路径内同时满足包含j和包含k
						dp[i][j] = min(dp[i][j],dp[i-(1<<j)][k]+w[k][j]);
					}
				}
			}
		}
	}
	
	cout << dp[(1<<n)-1][n-1] << endl;
}

---

树上dp

感觉上很类似状态压缩dp
按照儿子或者父亲的信息进行dp
遍历树的方法：dfs

• 状态表示$dp(u,j)$:

  • 集合$(u,j)$：所有以$u$为根的树的选择方案，其中：
    • $j=0$表示不选$u$
    • $j=1$表示选$u$
  • $dp(u,j)$就表示最大的快乐指数

• 状态转移：对于$u$，遍历其所有孩子$s$

  • $init:dp(u,0)=0;dp(u,0)+=max(dp(s,0),dp(s,1))$：上司不来，员工可来可不来
  • $init:dp(u,1)=happy[u];dp(u,1)+=dp(s,0)$：上司来，员工都不来

#include <bits/stdc++.h>
using namespace std;

const int N = 6010;

int n;
int happy[N];
int h[N],e[N],ne[N],idx;
int dp[N][2];
int indegree[N];//入度数组，判断根节点

void add(int a,int b){
	e[idx] = b;ne[idx] = h[a];h[a] = idx++;
}

void dfs(int u){
	dp[u][1] = happy[u];
	
	for(int i = h[u];i != -1;i++){
		int cur = e[i];
		dfs(cur);
		
		dp[u][0] += max(dp[cur][0],dp[cur][1]);
		dp[u][1] += dp[cur][0];
	}
}

int main(){
	scanf("%d",&n);
	for(int i = 1;i <= n;i++) scanf("%d",&happy[i]);
	
	memset(h,-1,sizeof h);
	for(int i = 0;i < n-1;i++){
		int a,b;
		scanf("%d%d",&a,&b);
		indegree[a]++;
		add(b,a);
	}
	
	int root = 1;
	while(indegree[root++]);//求根节点
	
	dfs(root);
	printf("%d\n",max(dp[root][0],dp[root][1]));
}

---

*记忆化搜索

动态规划专门解决子问题重复的问题
正常的动态规划是从小问题逐渐组合成为大问题的解
记忆化搜索就是反方向，从大问题向小问题递归，但每次遇到问题时

• 如果问题还没有被解决，就递归解决该问题，并且将解记录下来
• 如果改问题在之前的过程中被解决过，则直接在记录中查询该问题的解

所以记忆化搜索也被称为备忘录方法。

例题：

状态表示和状态转移斌没有本质上的差别，只有求解所有状态时有区别

• 状态表示$dp(i,j)$:

  • 集合$(i,j)$：所有从区域$(i,j)$开始滑的路径
  • $dp(i,j)$就表示最长路径

• 状态转移：分别判断能否向，前后左右滑雪，

  • $dp(i,j)=Max(dp(i+1,j),dp(i-1,j),dp(i,j+1),dp(i,j-1))+1$

现在采用递归的实现方式：

• 用一个特殊的数据来代表没有计算过
• 每一次递归求解小的问题

#include <bits/stdc++.h>
using namespace std;

const int N = 310;

int n,m;
int h[N][N];
int f[N][N];//动态规划数组

int dx[4] = {-1,0,1,0};
int dy[4] = {0,1,0,-1};

int dp(int x,int y){
	int &v = f[x][y];
	if(v != -1) return v;//之前算过，直接返回
	
	v = 1;
	for(int i = 0;i < 4;i++){
		int a = x+dx[i],b = y+dy[i];
		if(a >= 1 && a<=n && b>=1 && b<=n && h[a][b] < h[x][y]){
			v = max(v,dp(a,b)+1);
		}
	}
	
	return v;
}


int main(){
	scanf("%d %d",&n,&m);
	
	for(int i = 1;i <= n;i++){
		for(int j = 1;j <= m;j++){
			scanf("%d",&h[i][j]);
		}
	}
	
	memset(f,-1,sizeof f);
	
	int res = 0;
	for(int i = 1;i <= n;i++){
		for(int j = 1;j <= n;j++){
			res = max(res,dp(i,j));
		}
	}
	
	printf("%d\n",res);
}

优点：

• 思路简单，代码好写，主要是不用考虑遍历的顺序了

缺点：

• 时间复杂度和空间复杂度更高

提高班

数字三角形模型

• 考虑状态表示时，首先想到四维的状态$f[i_1,j_1,i_2,j_2]$，，比较难以考虑，可以选择让两个人同时行进，选择三维状态$f[k.,i_1,i_2]$，其中$k$是 步数-1
• 每次状态转移时，当前状态是由两个人向右或者向下转移来的，共四种选择$(R,R),(R,D),(D,R),(D,D)$.
• 另外如果有$i_1==i_2$，说明重合了，只用加一次当前的权重

for(int k = 2; k <= 2*n; k++) {
        for(int i1 = 1; i1 <= n; i1++) {
            for(int i2 = 1; i2 <= n; i2++) {
                int j1 = k-i1, j2 = k-i2;
                if(j1>=1&&j1<=n&&j2>=1&&j2<=n) {
                    int &x = f[k][i1][i2];
                    int t = w[i1][j1];
                    if(i1!=i2) t += w[i2][j2];
                    x = max(x, f[k-1][i1-1][i2-1]+t);
                    x = max(x, f[k-1][i1-1][i2]+t);
                    x = max(x, f[k-1][i1][i2-1]+t);
                    x = max(x, f[k-1][i1][i2]+t);
                }
            }
        }
    }

最长上升子序列模型

题目

怪盗基德

直接正向做一遍反向做一遍最长上升子序列

（反向也可以看作是做大下降子序列）

登山

本题是另一种形状，即先单调上升，后单调下降暂且称之为反"V"，自然的，对于这种形状的子序列，我们想到按照转折点是谁来进行分类

可以观察到
$$以a[i]结尾的反V最大长度=以a[i]结尾的最大上升子序列+倒过来看以a[i]结尾的最大上升子序列-1$$

所以思路是，先正向做一遍最大上升子序列，把结果保存到$f[i]$，再反向做最大上升子序列，把结果保存到$g[i]$，最后从头遍历一遍，找到最大的$f[i]+g[i]$。

友好城市

自行构建序列，选取一边的坐标作为自变量，取另一边的坐标作为因变量，以自变量为依据，将因变量排序，我们得到一个序列，该序列上的每一个上升子序列就对应一个合理的航线安排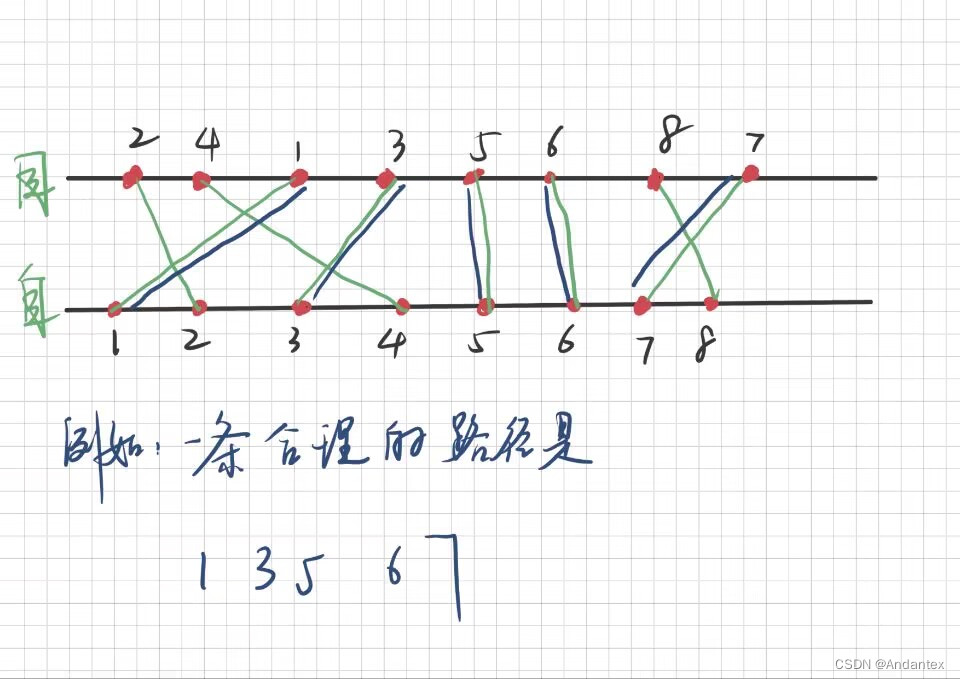

最大上升子序列和

更换状态数组存储的东西，令$f[i]$表示以$a[i]$结尾的上升子序列的和的最大值，状态转移与最大上升子序列相同

拦截导弹

• 第一问：最长下降子序列

• 第二问：贪心

  • 首先维护一个下降子序列组成的集合，考虑贪心：目标是让这个集合大小越小越好。先猜：使得每一个子序列的结尾越大越好
  • 依次扫描所有数字
    • 如果现有子序列都小于当前数，创建新的子序列
    • 如果存在结尾大于等于当前数的子序列，在其中选出结尾最小 的子序列，将当前数加入结尾（注意该做法意思是保证那些大的结尾尽可能不要变小）

• 贪心正确性说明：设贪心解是A，最优解是B

  • 显然$B\le A$
  • 要证明$A\le B$考虑调整法：
    • 找到第一个最优解方案和贪心法方案不同的数
    • 在贪心解和最优解中，该数位于的下降子序列的 前一位，一定满足 贪心$\le$最优解
    • 可以说，在最优解中，将该数（及该数后的一整个下降子序列）的位置，调整到与贪心解相同，不影响整个下降子序列集合的大小
    • 不断的进行以上调整，最终使得将最优解调整到贪心解，且没有引起整个集合变大
    • 于是我们可以说贪心解是一个最优解

• 第二问代码实现

  • 取$g[]$存储所有下降子序列的末尾值
  • 根据以上操作，每次在$g[]$中寻找比当前值大的最小数，将该数替换为当前数；或者将当前数加入$g[]$的末尾
  • 于是可以知道$g[]$保持单调递增，可以使用二分法

• 根据$Dilworth$定理。其实第二问就是求最大上升子序列个数

导弹防御系统

贪心+爆搜(dfs)

同时维护一个上升子序列集合的末尾数列和一个下降子序列集合的末尾数列，每次dfs时进行决策，是将当前数字加入上升子序列还是下降子序列

#include <iostream>
#include <algorithm>
using namespace std;

const int N = 55;

int n;
int q[N];
int up[N],down[N]; //上升子序列和下降子序列集合


int ans;

void dfs(int u,int su,int sd){ // 当前遍历到几，有几个上升子序列了，有几个下降子序列了
	if(su+sd >= ans) return; //剪枝
	if(u == n){//遍历结束
		ans = su+sd;
		return;
	}
	
	//将当前数放入上升子序列中
	int k = 0;
	while(k < su && up[k] >= q[u]) k++;
	int t = up[k];//存储变化前的状态
	up[k] = q[u];
	if(k < su) dfs(u+1,su,sd);//未增加序列
	else dfs(u+1,su+1,sd);
	up[k] = t;//dfs后恢复现场
	
	//将当前数放入下降子序列中
	k = 0;
	while(k < sd && down[k] <= q[u]) k++;
	t = up[k];//存储变化前的状态
	down[k] = q[u];
	if(k < sd) dfs(u+1,su,sd);//未增加序列
	else dfs(u+1,su,sd+1);
	down[k] = t;//dfs后恢复现场
}

int main(){
	while(cin>>n , n){
		for(int i = 0;i < n;i++) cin >> q[i];
		
		ans = n;
		dfs(0,0,0);
		
		cout << ans << endl;
	}
	return 0;
}

最长上升公共子序列

就是将两个问题结合到一起，从集合的观点来看，是两个问题的笛卡尔积

• 状态表示$f[i,j]$：由第一个序列的前$i$个字母，第二个序列的前$j$个字母中，且以$b[j]$ 结尾的 所有公共上升子序列的最大长度

• 状态转移：进行集合划分，然后对每一种情况取max。于是对于$f[i,j]$，能分成以下情况

  • 所有不包含$a[i]$的公共上升子序列：$f[i-1,j]$
  • 所有包含$a[i]$的公共上升子序列，这就说明$a[i]==b[j]$，可进一步进行划分
    • 按照最长公共上升子序列的倒数第二个数来进行划分，若倒数第二的数是$b[k],0\le k\le j-1$,则当前的状态是$f[i,k]+1$
    • 注意由于“上升”的条件，不是所有情况都符合条件

• 最后由于强行限制了$b[j]$结尾，需要遍历所有可能的$j$，找到全局最大值

for (int i = 1; i <= n; i ++ ) {
	for (int j = 1; j <= n; j ++ ) {
		f[i][j] = f[i - 1][j];//不包含a[i]
		if (a[i] == b[j]) {//包含a[i]
			int maxv = 1;//所有情况情况最烂是长度是1
			for (int k = 1; k < j; k ++ )
				if (b[j] > b[k])
					maxv = max(maxv, f[i - 1][k] + 1);
			f[i][j] = max(f[i][j], maxv);
		}
	}
}
int res = 0;
for (int i = 1; i <= n; i ++ ) res = max(res, f[n][i]);

三重循环，可以对其进行优化。首先注意到如果有a[i]==b[j]，则第三重循环只是循环中点与j有关。
观察maxv的行为，发现其是求了一个条件前缀最大值 M a x { f [ i − 1 ] [ k =    1 : j − 1 ]    s . t . a [ i ] > b [ k ] } Max\{f[i-1][k = \ \ 1:j-1] \ \ s.t.a[i]>b[k]\} Max{f[i−1][k=  1:j−1]  s.t.a[i]>b[k]}

所以完全可以把整个对maxv的求解提出来

for (int i = 1; i <= n; i ++ ) {
	int maxv = 1;
	for (int j = 1; j <= n; j ++ ) {
		f[i][j] = f[i - 1][j];
		if (a[i] == b[j]) f[i][j] = max(f[i][j], maxv);
		if (a[i] > b[j]) maxv = max(maxv, f[i - 1][j] + 1);
	}
}

关于上述代码的正确性：每次对ff[i][j]进行更新时，正好maxv也已经针对前j-1进行了更新，与上述我们要求的结果一致

题目联系

背包模型

面向题目建模时，重要的是找到什么是“重量”，什么是“价值”

装箱

令“重量”和“价值”都是集装箱体积，带入01背包

#include <iostream>
using namespace std;

const int V = 20000;
int n,v;
int f[V];

int main(){
	cin >> v >> n;
	for(int i = 1;i <= n;i++){
		int w;
		cin >> w;
		for(int j = v;j >= w;j--) f[j] = max(f[j],f[j-w]+w);
	}
	cout << v-f[v] << endl;
}

宠物小精灵

首先选出重量和价值：

• 二维重量：消耗精灵球数$m_i$，消耗皮卡丘生命值$k_i$
• 价值：精灵数量(每个精灵都为1)
• 状态表示: $只在前i个小精灵中捕捉，使用精灵球数不超过j，皮卡丘掉血不超过k,能获得的最大精灵数量f(i,j,k)=Max(f(i-1,j,k),f(i-1,j-m_i,k-k_i)+1)$

把第一个维度滚掉

#include <iostream>
#include <algorithm>
using namespace std;

const int N = 1010, M = 510;

int n, V1, V2;
int f[N][M];

int main()
{
	cin >> V1 >> V2 >> n;
	for (int i = 0; i < n; i ++ )
	{
		int v1, v2;
		cin >> v1 >> v2;
		for (int j = V1; j >= v1; j -- )
			for (int k = V2 - 1; k >= v2; k -- )
				f[j][k] = max(f[j][k], f[j - v1][k - v2] + 1);
	}
	
	cout << f[V1][V2 - 1] << ' ';
	int k = V2 - 1;
	while (k > 0 && f[V1][k - 1] == f[V1][V2 - 1]) k -- ;
	cout << V2 - k << endl;
	
	return 0;
}

还能再优化，参考题解

潜水

• 多维重量+限制反转，费用1：氧气；费用二：氮气；价值：重量

  • 这启发我们找价值和重量时不能找大小关系，比如这题就是“$费{用}_1\ge m，费{用}_2\ge n，求价值的最小值$”
  • 一般是“限制量”是重量，“目标量”是价值

• 状态表示：$选前i罐，氧气恰好是j，氮气恰好是k，最小的重量f(i,j,k)=Min(f(i-1,j,k),f(i-1,j-a_i,k-b_i)+c_i)$ 这么做是过不的

  #include <iostream>
  #include <algorithm>
  #include <cstring>
  
  using namespace std;
  
  const int N = 50, M = 160;//错
  
  int n,m,K;
  int f[N][M];
  
  int main()
  {
  	cin >> n >> m >> K;
  
  	memset(f,0x3f,sizeof(f));
  	f[0][0] = 0;
  
  	for (int i = 0; i < K; i ++ )
  	{
  		int v1, v2, w;
  		cin >> v1 >> v2 >> w;
  		for (int j = N-1; j >= v1; j -- )
  			for (int k = M - 1; k >= v2; k -- )
  				f[j][k] = min(f[j][k], f[j - v1][k - v2] + w);
  	}
  
  	int res = 1e9;
  	for(int i = n;i < N;i++){
  		for(int j = m;m < M;j++){
  			res = min(res,f[i][j]);
  		}
  	}
  
  	cout << res << endl;
  
  	return 0;
  }
  
  

  • 初始化：其目的主要是为了初始化所有的$f(0,j,k)$为正无穷，$f(0,0,0)$为0

    • 这是因为状态$f(0,j,k)$意思是$什么都不选，且氧气恰好是j，氮气恰好是k$，这是一个非法状态。对于这种状态的处理，就是赋给一个不可能作为答案的数。比如这里是无穷大
    • 无穷大还有一个好处是，所有从非法状态转移来的状态正好也都是无穷大了

  • 按理说循环应该发生在区间$[m,+\infty )$，但是实际上只用枚举到 f ( n × M a x { a i } , m × M a x { b i } ) f(n\times Max\{a_i\},m \times Max\{b_i\}) f(n×Max{ai​},m×Max{bi​})

    • 考虑最差情况，每一罐气体都是 ( 1 , M a x { b i } ) (1,Max\{b_i\}) (1,Max{bi​})，这样为了凑出$m$,则第二维必须开到 m × M a x { b i } m \times Max\{b_i\} m×Max{bi​}，第一维的讨论同理
    • 但是显然爆掉了，说明该方法并不可行

  • 获得最终答案时，需要手动遍历所有合理的状态，获得最小值。

• 状态表示：$选前i罐，氧气不少于j，氮气不少于k，最小的重量f(i,j,k)=Min(f(i-1,j,k),f(i-1,j-a_i,k-b_i)+c_i)$

  #include <cstring>
  #include <iostream>
  
  using namespace std;
  
  const int N = 22, M = 80;
  
  int n, m, K;
  int f[N][M];
  
  int main()
  {
  	cin >> n >> m >> K;
  
  	memset(f, 0x3f, sizeof f);
  	f[0][0] = 0;
  
  	while (K -- )
  	{
      	int v1, v2, w;
      	cin >> v1 >> v2 >> w;
      	for (int i = n; i >= 0; i -- )
          	for (int j = m; j >= 0; j -- )
              	f[i][j] = min(f[i][j], f[max(0, i - v1)][max(0, j - v2)] + w);
  	}
  
  
  	cout << f[n][m] << endl;
  
  	return 0;
  }
  

  • 初始化还是一样的，把合法的状态初始化成无穷大

  • 为什么不用像上一个状态表示一样循环到更大的地方？

    • 更大的状态没有意义了。

  • 为什么要循环到0？

    • 接下来我们假想一个一维重量的情形。第$i$个物品的重量是$w_i$，价值是$q_i$。

    • 目前遇到有一个情形，目前是针对第$i$个物品进行更新，该物品的重量是$4$，试图更新的是f[2]

      • 不管状态表示是“不多于”，还是“恰好是”。都不可能用当前物品更新状态：因为语义上就不满足
      • 但是如果状态表示是“不少于”，那就可以用当前物品更新状态。更进一步思考，这一步只有两种可能
        • 不更新f[2]，即不选择这个物品。
        • 更新。这个情况只会在这个物品的重量比之前f[2]代表的状态的所有物品价值之和还要少。所以更新的方式是，只选这个物品，把之前的全扔掉。即把f[2]更新成值$q_i$

    • 意思是在之前的状态表示里，$f[\le w_i]$的状态是没必要进行更新的。但是在“不大于”的状态表示里，这些状态都有可能被更新

  • f[i][j] = min(f[i][j], f[max(0, i - v1)][max(0, j - v2)] + w)什么操作？

    • 沿用上一问的理解，假想一个一维重量的情形。第$i$个物品的重量是$w_i$，价值是$q_i$。
    • 这里其实在干的事情是，对于所有$f[\le w_i]$的状态，我看看需不需要更新。如果需要更新，就直接更新成当前的价值$q_i$，这是因为f[0]被初始化为0
      • 这正好与我们在上一问的讨论吻合
    • 还有一种理解是，f[负数]状态与f[0]没有区别。因为在物品重量非负的情况下，“不少于一个负数重量”和“重量不少于0”是等价的。

有依赖的背包问题

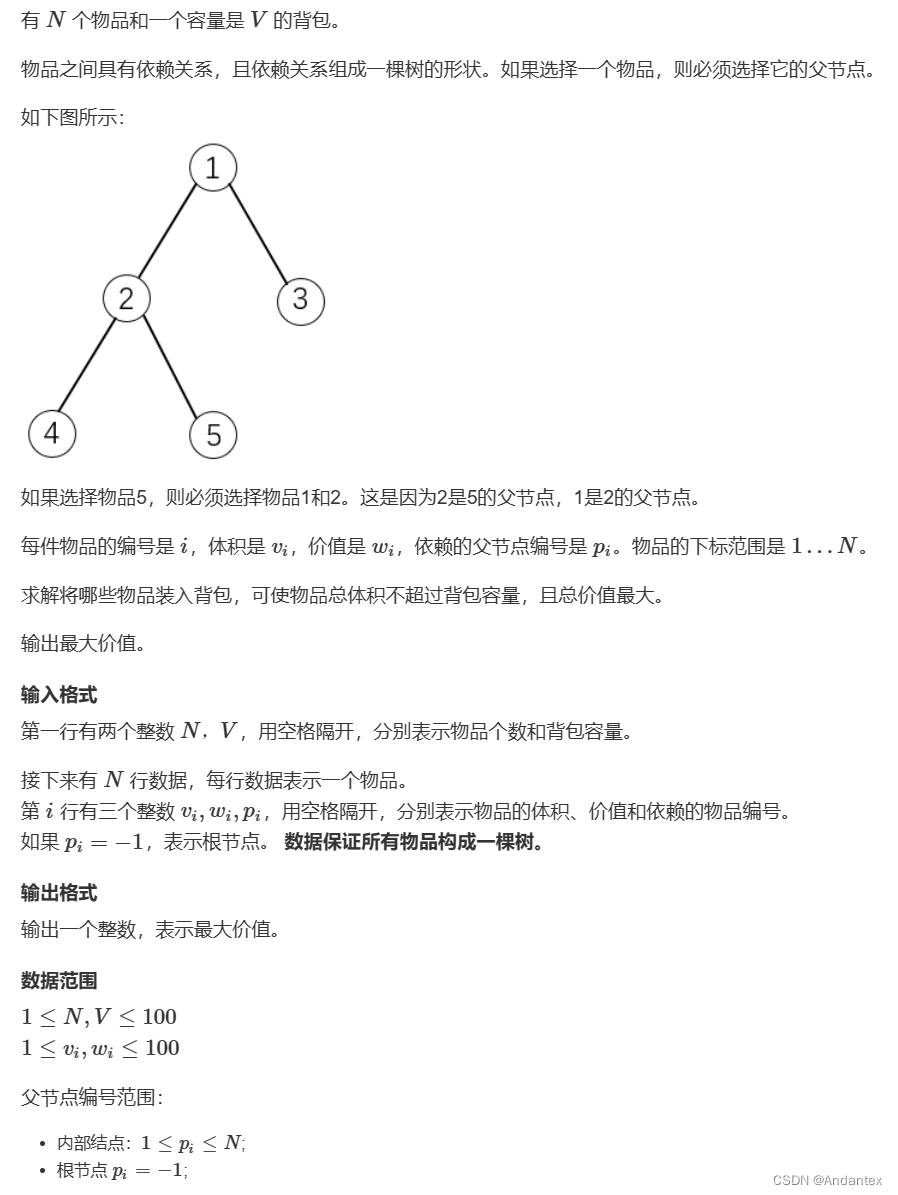
背包问题+树形bp

• 首先进行一个重要的论断：如果要选择以节点$i$为根的子树中的任何节点，则必须选择$i$
• 以此为入口选择状态表示$f(i,j):考虑以节点i为根的子树，在总体积不大于j的情况下，所能选择的最大价值$
• 状态转移：考虑尾部决策，在这里是某个子树选不选，选哪个状态用于转移
  • 首先dfs处理好所有子树
  • 因为节点$i$是必选的，先将f[i][v[i]~m]初始化为w[i]
  • 对于某个子树
    • 该子树有很多状态，是f[son][0~m]
    • 此时将问题视为一个分组背包问题，将一个子树中的所有状态视为一组，该组中只能选择一个f[son][k]来进行状态转移
  • 考虑遍历所有可能的体积大小，由于我们在接下来的内部是做一次分组背包，所以需要滚动数组，反向循环for(int j = m;j >= v[i];j--)
  • 对于每一个体积$j$对应的状态f[i][j]
    • 考虑选择子树的什么状态比较合适，因为要为树根留出重量，所以k取[0~j-v[i]]

#include <bits/stdc++.h>
using namespace std;

const int N = 110;


int f[N][N];
vector<int> h[N];
int v[N],w[N];
int n,m,root;

void dfs(int u){
    for(int i = v[u];i <= m;i++) f[u][i] = w[u];
    
    for(auto son:h[u]){
        dfs(son);
        for(int j = m;j >= v[u];j--){
            for(int k = 0;k <= j-v[u];k++){
                f[u][j] = max(f[u][j],f[u][j-k]+f[son][k]);
            }
        }
    }
}

int main(){
    cin >> n >> m;
    for(int i = 1;i <= n;i++){
        int p;
        cin >> v[i] >> w[i] >> p;
        if(p == -1) root = i;
        else h[p].push_back(i);
    }
    dfs(root);
    cout << f[root][m] << endl;
}

能量石

贪心+动规

该题涉及到了两个维度，一个是时间上的排列，一个是集合子集的选取。将该题分成两步走

• 考虑先将所有能量石排列好，即决定好先后顺序
• 再从排列好的能量石中选取一个子集吃

这么做的原因是第一步可以通过贪心解决，参考耍杂技的牛

• 考虑两个能量石$x,y$，
  • 如果先吃$x$，获得总价值是$E_x+E_y-S_x{L}_y$
  • 如果先吃$y$，获得总价值是$E_x+E_y-S_y{L}_x$
  • 这样经过一通运算，得到先吃$x$的情形需要是$\frac{S_x}{L_x}\le \frac{S_y}{L_y}$
• 所以可以先进行贪心，将所有石头先按照$\frac{S_i}{L_i}$从小到大排列
• 再进行dp，此时考虑状态表示：首先应该保存选了什么能量石，其次应该保存时间的信息。所以考虑$f(i,j)为：从前i个能量石中选择，且使用时间恰好是j，所能获得的最大能量$
  • 状态转移，对于某个能量石，仍然是选或者不选的问题$f(i,j)=Max(f(i-1,j),(f(i-1,j-S_i)+E_i-L_i(j-S_i){)}_{+})$
  • 注意事项：能量石能量不能为负
• 注意dp终点，需要将所有的$S_i$加起来作为第二维的最大值
• 同时最后需要遍历全体，找到最大值

#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 105, S = 10005;
int n;
int f[S];
struct Node{
    int s, e, l;
    bool operator < (const Node &x) const{
        return s * x.l < x.s * l;
    }
}a[N];
int main() {
    int T, cnt = 0; scanf("%d", &T);
    while(T--) {
        memset(f, 0xcf, sizeof f);
        scanf("%d", &n);
        int t = 0;
        for(int i = 1, s, e, l; i <= n; i++) {
            scanf("%d%d%d", &s, &e, &l);
            t += s; a[i] = (Node) { s, e, l }; 
        }
        sort(a + 1, a + 1 + n);
        f[0] = 0;
        for(int i = 1; i <= n; i++) {
            for(int j = t; j >= a[i].s; j--)
                f[j] = max(f[j], f[j - a[i].s] + max(0, a[i].e - (j - a[i].s) * a[i].l));
        }
        int res = 0;
        for(int i = 1; i <= t; i++) res = max(res, f[i]);
        printf("Case #%d: %d\n", ++cnt, res);
    }
    return 0;
}