第五周：函数和代码复用

初_霁

已于 2024-11-10 15:36:18 修改

阅读量1.1k

点赞数 14

文章标签： python 笔记

于 2024-10-21 19:27:44 首次发布

本文链接：https://blog.csdn.net/DA_CK/article/details/143125899

版权

第五周：函数和代码复用

1. 函数的理解和调用

函数是一段代码的表示，是一段具有特定功能的，可重用的语句组，一种功能的抽象，一般函数表达特定功能，由保留字 def 和 return 定义

python 解释器自带一些函数，称为 python 的标准函数，如：abs(),pow(),len()

作用：降低编程难度和代码复用

def <函数名>（<参数列表>）:#参数列表也称形参，相当一个占位符，代指输入的数据，当函数被调用时，实际传递给函数内部的值，称为实参
    <函数体>#这是函数执行的代码
    return<返回值列表>#需要返回值列表时写入，没有可以省略
#函数名符合python命名规则
#参数列表是调用函数时输入的值，可以有零个或多个，当传递多个参数时用逗号隔开，没有参数时也要保留圆括号
#执行return语句或函数体结束后，程序的控制权返回到调用函数的位置

def f():
    pass
#pass仅占位，不表任何操作

def isprime(n):
    if n < 2:
        return False
    for i in range(2,n//2 +1):
        if n % i == 0:
            return False
    return True
#前7行不直接执行，解释器会记录isprime()的位置，为后续调用作准备
#当一个函数被调用时，此时执行的程序会暂停执行
count = 0
for i in range(1,10000):
    if isprime(i):
        count += 1
print(count)
#神奇的是在line4，自[n//2+1,n)都不会被整除，故将n//2+1换成n也行，只不过遍历的时间更长

def fact(n):
    s = 1
    for i in range(1,n+1):
        s *= i
    return s
#调用 a = fact(10)\print(a)

y=f(x)

函数定义时，所指的参数是一种占位符，如果不经过调用，不会被执行，参数是输入，函数体是处理，结果是输出（IPO）

2. 函数参数的传递

函数可以有参数，也可以没有，但必须保留括号

#函数定义时可以为对某些参数指定默认值,构成可选参数
#如果参数定义了默认值，当函数被调用时，若没有传入对应的参数值，则使用默认值
def <函数名>	(<非可选参数>,<可选参数>):
    <函数体>
    return(返回值)

>>>def dup(str,times = 2):#str为非可选参数，times为可选参数
       print(str*times)
>>>dup("knnock~")
knock~knock~
>>>dup("knock~",4)
knock~knock~knock~knock~
#可选参数必须在非可选参数之后

def fact(n,m=1):
    s = 1
    for i in range(1,n+1):
        s *= i
    return s//m
#m给值即值，否则视为1

#函数定义时可以设计可变数量参数，即不确定参数总数量
def <函数名>（<参数>，*b）:
    <函数体>
    return<返回值>

def fact(n,*b):
    s = 1
    for i in range(1,n+1):
        s *= i
    for item in b:
        s *= item
    return s
>>>fact(10,3)
10886400#先算出10的阶乘，再乘3
>>>fact(10,3,5,8)#这里的可变参数被当作元组类型
435456000#先算出10的阶乘，再乘3乘5乘8

#对标准函数max(x1,x2,x3...)这种不确定参数数量的，可利用可变参数的函数

函数调用时，参数可以按照位置或名称方式传递

>>>func(x1,y1,z1,x2,y2,z2)
    return(x1*x2 + y1*y2 + z1*z2)
result = func(1,2,3,4,5,6)

#<函数名>(<参数名> = <实际值>)
>>>result = func(x1=1,x2=2,y1=2,y2=5,z1=3,z2=6)

3. 函数的返回值

函数可以返回 0 或多个结果

return 保留字用来退出函数执行并传递返回值

函数可以有返回值，也可以没有，可以有 return，也可以没有

return 可以传递 0 个返回值，也可以传递任意多个返回值，此时多个值以元组类型返回

>>>def func(a,b):
       return a*b
>>>s = func("knock~",2)
>>>print(s)
knock~knock~

>>>def func(a,b)
   return b,a
>>>s = func("konck",2)
>>>print(s,type(s))
(2,'konck')<class'tuple'>

def fact(n,m=1):
    s = 1
    for i in range(1,n+1):
        s *= i
    return s//m,s,m
>>>fact(10,5)
(725760,3628800,5)#元组类型
>>>a,b,c = fact(10,5)
print(a,b,c)
725760 3628800 5

4. 局部变量和全局变量

n,s = 10,100#n和s是全局变量
def fact(n):
    s = 1#fact中的n和s是局部变量，函数参数也是局部变量
    for i in range(1,n+1):
        s *= i
    return s
print(fact(n),s)#n和s是全局变量
>>>3628800 100

规则 1:局部变量和全局变量是不同变量

局部变量是函数内部的占位符，与全局变量可能重名但不同

函数运算结束后，局部变量被释放

可以使用 global 保留字在函数内部对全局变量赋值或重新创建

n = 2#n在函数外部，可认为是全局变量
def func(a,b):
    global n
    n = a*b
    return a*b
print(func("knock~",2))
knock~knock~
print(n)
knock~knock~

n = 2
def fucn(a,b):
    return a*b*n
print(fucn("knock~",2))
knock~knock~knock~knock~

规则 2:局部变量为组合数据类型且未创建，等同于全局变量

ls = ["F","f"]#通过使用[]真实创建了一个全局变量列表ls
def func(a):
    ls.append(a)#此时ls是列表类型，未真实创建则等同于全局变量
    return
func("C")#全局变量ls被修改
print(ls)
>>>['F''f''C']
#原因是组合数据类型有创建和引用的区别，只有使用赋值或list创建才有真实，否则为之前创建的一次引用
#函数内不存在变量ls的创建过程，此时func()函数专属的内存空间中没有已经创建过且名称为ls的列表，
#因此，fucn()函数进一步去寻找全局内存空间，自动关联外部列表变量ls，并修改对应值

ls = ["F""f"]
def func(a):
    ls = []
    ls.append(a)
    return
func("C")
print(ls)
>>>['F''f']

总结：

函数内变量无论是否与全局变量重名，若在函数内部创建，函数退出后变量被释放，如与全局变量重名，全局变量的值不变
全局变量可以不用 globle 声明，直接在函数内部使用
当需要在函数内部对全局变量赋值或重新创建时，使用保留字 global 在函数内部声明全局变量
对于组合数据类型，如列表类型，当组合数据类型采用引用方式使用，不采用 global 声明时，函数内可以通过方法或操作函数等方式改变全局变量

扩展(指针和引用)：

指针是保存内存地址的变量
引用是某一变量的别名，用这个名字可以对变量进行操作
区别：指针直接指向内存地址，说明对象已经生成，而引用只是别名，需要真实创建对象才能操作对象

5.lambda(匿名)函数

lambda 函数返回函数名作为结果

使用 lambda 保留字定义，函数名是返回结果

lambda 函数用于定义简单、能够在一行内表示的函数

<函数名> = lambda<参数>:<表达式>#紧凑形式
#普通形式
def <函数名>（<参数列表>）:
    <函数体>
    return<返回值>

>>>f = lambda x,y:x+y
>>>f(10,15)
25
>>>f = lambda : "lambda函数"
>>>print(f())
lambda函数

谨慎使用 lambda 函数

lambda 函数主要用于一些特定函数或方法的参数

lambda 函数有一些固定使用方式，建议逐步掌握

一般情况，建议使用 def 定义普通函数

6.map()函数

#map(f,iters)它用于将函数功能f逐一作用于组合类型参数iters的各元素
>>>"".join(map(lambda i:i*2,"123"))
'112233'
>>>list(map(lambda i:i*2,[1,2,3,4,5]))
[2,4,6,8,10]
#map函数的第一个参数为函数名，一般由lambda()函数表达

7. 实例七：七段代码管绘制

  __A__
 |      |
 F      B
 |__G__ |
 |      |
 E      C
 |__D__ |
#绘制顺序：GCDEFAB

import turtle
def drawLine(draw):#绘制单段数码管
    turtle.pendown() if draw else turtle.penup()
    turtle.fd(40)
    turtle.right(90)
def drawDigit(digit):#根据数字绘制七段数码管
    drawLine(True) if digit in [2,3,4,5,6,8,9] else drawLine(False)
    drawLine(True) if digit in [0,1,3,4,5,6,7,8,9] else drawLine(False)
    drawLine(True) if digit in [0,2,3,5,6,8,9] else drawLine(False)
    drawLine(True) if digit in [0,2,6,8] else drawLine(False)
    turtle.left(90)
    drawLine(True) if digit in [0,4,5,6,8,9] else drawLine(False)
    drawLine(True) if digit in [0,2,3,5,6,7,8,9] else drawLine(False)
    drawLine(True) if digit in [0,1,2,3,4,7,8,9] else drawLine(False)
    turtle.left(180)
    turtle.penup()#为绘制后续数字确定位置
    turtle.fd(20)#为绘制后续数字确定位置
def drawDate(date):#获得输出的数字
    for i in date:
        drawDigit(eval(i)) #通过eval函数将数字变为整数
def main():
    turtle.setup(800,350,200,200)
    turtle.penup()
    turtle.fd(-300)
    turtle.pensize(5)
    drawDate('2024917')
    turtle.hideturtle
    turtle.done()
main()

import turtle,time
def drawGap():
    turtle.penup()
    turtle.fd(5)
def drawLine(draw):#绘制单段数码管
    drawGap()
    turtle.pendown() if draw else turtle.penup()
    turtle.fd(40)
    drawGap()
    turtle.right(90)
def drawDigit(digit):#根据数字绘制七段数码管
    drawLine(True) if digit in [2,3,4,5,6,8,9] else drawLine(False)
    drawLine(True) if digit in [0,1,3,4,5,6,7,8,9] else drawLine(False)
    drawLine(True) if digit in [0,2,3,5,6,8,9] else drawLine(False)
    drawLine(True) if digit in [0,2,6,8] else drawLine(False)
    turtle.left(90)
    drawLine(True) if digit in [0,4,5,6,8,9] else drawLine(False)
    drawLine(True) if digit in [0,2,3,5,6,7,8,9] else drawLine(False)
    drawLine(True) if digit in [0,1,2,3,4,7,8,9] else drawLine(False)
    turtle.left(180)
    turtle.penup()#为绘制后续数字确定位置
    turtle.fd(20)#为绘制后续数字确定位置
def drawDate(date):#获得输出的数字
    turtle.pencolor("red")
    for i in date:
        if i =='-':
            turtle.write("年",font=("Arial",18,"normal"))
            turtle.pencolor("green")
            turtle.fd(40)
        elif i == '=':
            turtle.write("月",font=("Arial",18,"normal"))
        elif i == '+':
            turtle.write("日", font=("Arial", 18, "normal"))
        else:
            drawDigit(eval(i))
def main():
    turtle.setup(800,350,200,200)
    turtle.penup()
    turtle.fd(-300)
    turtle.pensize(5)
    drawDate(time.strftime("%Y-%m=%d+",time.gmtime()))
    drawDate('2024917')
    turtle.hideturtle
    turtle.done()
main()

无论每段数码管是否被绘制出来，画笔都会走过每一段，根据紧凑形式判段数字是否符合绘制

扩展：

计算机硬件时钟，断电时间的准确性问题，主板上有纽扣电池，有必要时操作系统会从硬件时钟中读出时间放入内核给应用软件使用

7. 抽象和代码复用

抽象是一种代码定义，用来赋予代码含义，主要包括函数和对象两种方式

分别对应面向过程(过程式)和面向对象(对象式)编程思想

代码复用：把代码当成资源进行复用

代码资源化：程序代码是一种用来表达计算的" 资源"

代码抽象化：使用函数等方法对代码赋予更高级别的定义

代码复用：同一份代码在需要时可以被重复使用

函数和对象是代码复用的两种主要形式

函数：将代码命名；在代码层面建立了初步抽象

对象：属性和方法；<a>.<b>和<a>.<b>()在函数之上再次组织进行抽象

8. 模块化设计:分而治之

通过函数或对象封装将程序划分为模块及模块之间的表达；具体包括主程序，子程序和子程序之间的关系；分而治之是一种分层抽象、体系化的设计思想；七段数码管绘制就是最好的体现

#DrawSevenSegDisplay.py
import turtle as t
import time
def drawGap():#绘制数码管间隔
    t.penup()
    t.fd(6)
def drawLine(draw):#绘制单段数码管
    drawGap()#这样产生数码管的效果(空格)，否则仅仅为完整的线
    t.pendown() if draw else t.penup()#紧凑形式<表达式1> if <条件> else <表达式2>
    t.fd(40)
    drawGap()#这样数码管两边都会有空隙，不会很突兀
    t.right(90)
def drawDight(d):#根据数字绘制单段的数码管
    drawLine(True) if d in [2,3,4,5,6,8,9] else drawLine(False)
    drawLine(True) if d in [0,1,3,4,5,6,7,8,9] else drawLine(False)
    drawLine(True) if d in [0,2,3,5,6,8,9] else drawLine(False)
    drawLine(True) if d in [0,2,6,8] else drawLine(False)
    t.left(90)
    drawLine(True) if d in [0,4,5,6,8,9] else drawLine(False)
    drawLine(True) if d in [0,2,3,5,6,7,8,9] else drawLine(False)
    drawLine(True) if d in [0,1,2,3,4,7,8,9] else drawLine(False)
    t.left(180)
    t.penup()
    t.fd(20)
def drawDate(date):#遍历日期字符串
    t.pencolor("red")
    for i in date:
        if i == "-":
            t.write("年",font=("Arial",18,"normal"))
            t.pencolor("blue")
            t.fd(40)
        elif i == "=":
            t.write("月",font=("Arial",18,"normal"))
            t.pencolor("green")
            t.fd(40)
        elif i == "+":
            t.write("日",font=("Arial",18,"normal"))
            pass#啥也不干
        else:
            drawDight(eval(i))#记得去引号，将字符串变数字
def main():
    t.setup(800,350,200,200)
    t.penup()
    t.fd(-300)
    t.pensize(5)
    drawDate(time.strftime("%Y-%m=%d+",time.gmtime()))#gmtime()返回当前时间戳对应的 struct_time 类型，\
    # strftime时间式化模版字符串，用来定义输出效果
    t.hideturtle()#隐藏海龟图标，虽然放在这里没啥用
main()
t.done()
'''
采用函数封装后，理解程序的第一层不再是直接阅读一行行语句，而是通过函数阅读程序框架
理解函数所表达的功能及调用关系，当需要了解具体函数内部实现时，再进一步理解函数内部语句
'''

模块化设计以功能块为基本单位，一般有以下俩个基本要求:

紧耦合：两个部分之间交流很多，无法独立存在，尽可能合理划分功能块，功能块内部耦合紧密

松耦合：两个部分之间交流和少，可以独立存在，模块间关系尽可能简单，功能块之间耦合度低

模块内部紧耦合，模块之间松耦合

9. 函数递归

函数定义中调用函数自身的方式，例如 n!

n! = n(n-1)(n-2)....1 <=> n(n-1)!

函数在定义中调用自身的方式称为递归调用，简称递归。包含递归调用的函数称为递归函数。

两个关键特性：

递归链条：递归链条在函数中表达递归调用关系，所有递归链条均以一个或多个基例结尾

递归基例：是不需要再次递归的确定值或确定表达式。可能存在一个或多个基例，例如 0！= 1

递归的实现：函数+分支语句

if <基例条件>:
    <返回：基例值>
else:
    <构造：递归链>
#参考下面
   - 1基例值  n=0基例条件
n!|
   - n(n-1)!递归链  其他

递归本身是一个函数，需要函数定义方式描述

函数内部，采用分支语句对输入参数进行判断

基例和链条，分别编写对应代码

def fact(n):
    if n == 0:
        return 1
    else:
        return n*fact(n-1)
n = eval(input("请输入数字"))
print(fact(n))

递归不提高程序执行效率,每次函数调用时，函数参数独立存储，递归中各次函数相互没有影响

任何递归程序都可以通过堆栈或队列变成非递归程序（这是程序的高级应用）

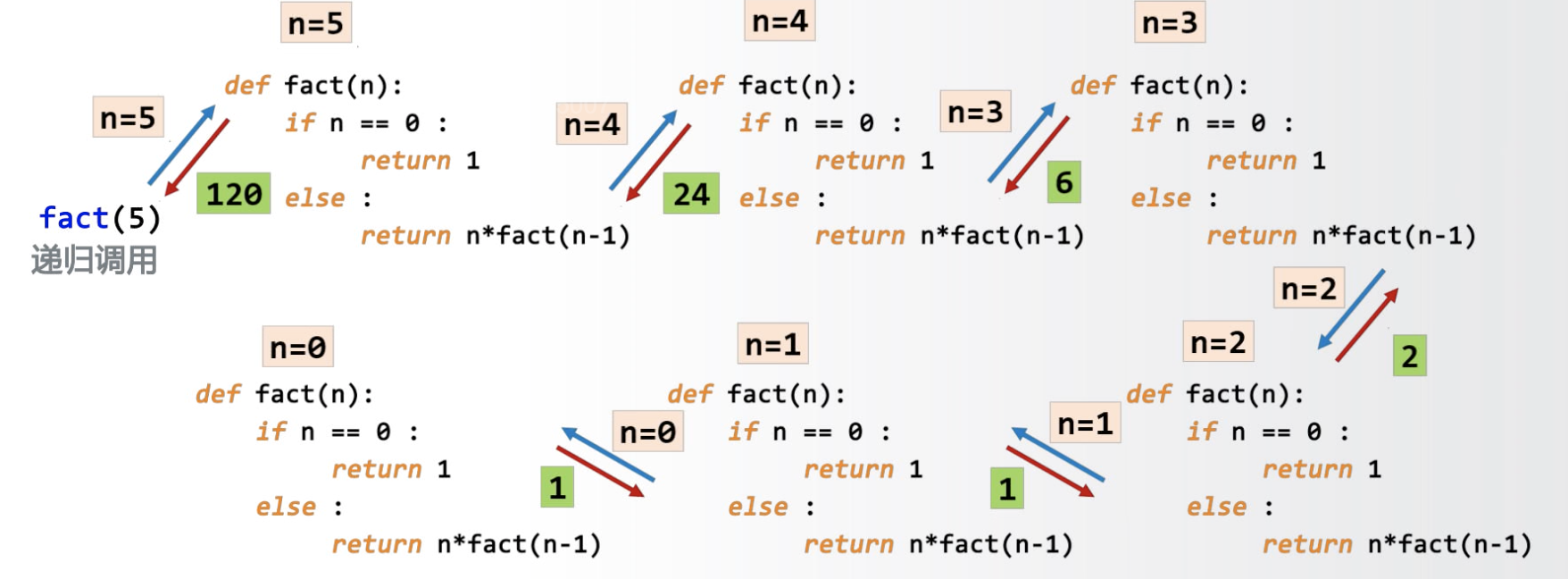
10. 函数递归实例解析

将字符串 s 反转后输出

>>>s[::-1]

def rvs(s):#得到递归变量为字符串s及其长度n
    if s =="":#完成递归基例的设置
        return s#一般来说，能够直接获得结果的情况都可以作为递归基例，所有递归基例不止一个
    else:
        return rvs(s[1:])+s[0]#这里又调用了rvs函数，实现了函数的递归
str = input("请输入一个字符串:")
print(rvs(str))
#故根据line3注释，认为当只有最后一个字符时，其反转也为自身，相当于一个基例
def reverse():
    if len(s) <= 1:
        return s
    else:
        return reverse(reverse(1:) + s[0])
str = input("请输入一个字符串:")
print(reverse(str))

#定义F(0)=1,F(1)=1,F(n)=F(n-2)+F(n-1),n>=2
#第一章的代码
a,b = 1,1
while a < 1000:
    print(a,end="")
    a,b = b,a+b
#F(n)=F(n-1)+F(n-2)
def F(n):
    if n < 2:
        return 1
    else:
        return F(n-1) + F(n-2)
n = eval(input("请输入数字:"))
for i in range(n):
    print(F(i),end=" ")

count = 0
def hanoi(n,src,dst,mid):#src源柱，dst目标柱，mid过渡柱
    global count#声明全局变量，才能使用，函数里面的只有括号里定义的以及函数内产生的变量
    if n==1:#当只有一个圆盘时
        print("{}:{}->{}".format(1,src,dst))#圆盘尺寸:从源柱搬到目标柱
        count += 1
    else:#即盘数>=2时
        hanoi(n-1,scr,mid,dst)#再次调用汉诺塔，以除最下面圆盘外的为目标，此时相当于重置汉诺塔问题，要求为从源柱向过渡柱搬运，目标柱反而为"过渡柱"
        print("{}:{}->{}".format(n.src,dst))#n为圆盘尺寸，相当于特指那个盘,n越大圆盘尺寸越大
        count += 1
        hanoi(n-1,mid,dst,src)#当进行完n-1数量的圆盘搬运后，再以中间柱为源柱向目标柱搬运，源柱相当于过渡柱
hanoi(3,"A","C","B")
print("总步数为:",count)
'''
请输入圆盘总数:3
1:A->C
2:A->B
1:C->B
3:A->C
1:B->A
2:B->C
1:A->C
总步数为: 7
'''

11.Python标准函数

3.13.0 Documentation Python文档

Python 提供 71 个标准函数，这些函数可以直接调用

A	B	C	D	E
abs() aiter() all() anext() any() ascii()	bin() bool() breakpoint() bytearray() bytes()	callable() chr() classmethod() *compile() complex()	delattr() dict() dir() divmod()	enumerate() eval() exec()
F	H	L	M	N
filter() float() format() *frozenset()	hasattr() hash() help() hex()	len() list() *locals()	map() max() *memoryview() min()	*next()
O	P	R	S	T
object() oct() open() ord()	pow() print() *property()	range() repr() reversed() round()	set() setattr() slice() sorted() *staticmethod() str() sum() super()	tuple() type()
V	Z	_
*vars()	zip()	*__import()__

12.PyInstaller 库

概述：

Pyinstaller 库是一个将 Python 源文件打包成可执行文件的第三方库，可用于多种操作系统，好处是不用配置环境

pip install pyinstaller#安装
pip install --upgrade pyinstaller#更新

PyInstaller Manual — PyInstaller 6.11.0 documentation 此库地址

pyinstaller -F <文件名.py>
#实际上不需要在终端输入<>

之后的目录下会多出三个文件：_pycache_;build;dist 前两个可以放心删除，在 dist 中，可以看到与原文件名相同的 exe 文件，这个便是我们打包的文件

build 目录是 pyinstaller 储存临时文件的目录，可以删除。最终打包程序在 dist 内部的 xx 中。目录中的其他文件是 xx 执行所需的动态链接库。

扩展：动态链接使程序在运行时调用不属于其程序的代码，进而程序会十分简洁，Windows 提供大量动态链接库，一般以 dll 或 ocx 为扩展名

注意：文件路径不能出现空格和英文句号;源文件必须为 UTF-8 编码

程序打包:

参数	描述
-F,--onefile	在 dist 文件夹中只生成独立的打包文件,不依赖库文件
-D DIR--onedir	默认值，生成 dist 目录 --distpath
-i<.ico or .icns>	指定打包程序使用的图标(icon)文件
-h，--help	查看帮助
--clean	清理打包过程中的临时文件
-v,--version	查看 pyinstaller 版本

对于我能用的
-F#打包文件
--distpath#默认目录
--icon icon.icns#icon指图标，icon后面的表示自己的icns文件名

对我的注意:不知道为什么，-D 在我这里总是错误，换成--distpath 就行了

在线生成 ico 文件:https://www.bitbug.net/

不过苹果是 icns 文件

#不知道为什么我的设置不行，以下是我的解决方案
pyinstaller --onefile --windowed --icon icon.icns --name testApp main.py
--onefile参数表示生成一个单独的可执行文件，
--windowed参数表示生成一个无控制台窗口的应用程序（对于GUI应用程序很有用），
--icon参数后面紧跟图标文件的名称（如果图标文件与脚本在同一目录下），
--name参数用于指定生成的应用程序的名称。testApp 为更改后的文件名，main.py为要更改的文件

13. 实例八:科赫雪花小包裹

分形几何：一种迭代的几何图形，广泛存在于自然界中

#DrawKoch.py
import turtle as t
def koch(size,n):
    if n==0:
        t.fd(size)
    else:
        for angle in [0,60,-120,60]:
            t.left(angle)
            koch(size/3,n-1)
def main():
    rank = 3#阶数
    t.setup(800,400)
    t.speed(-20)#控制画笔速度,0最快，1-10数字大速度快
    t.penup()
    t.goto(-300,-50)
    t.pendown()
    t.pensize(2)
    koch(600,rank)#绘制曲线
    t.hideturtle()#隐藏海龟
main()
t.done()

#DrawKochV1.py
import turtle
def koch(size,n):
    if n == 0:
        turtle.fd(size)
    else:
        for angle in [0,60,-120,60]:
            turtle.left(angle)
            koch(size/3,n-1)
def main():
    turtle.setup(600,600)#默认生成窗口在中央，仅仅设置了宽高
    turtle.penup()
    turtle.goto(-200,100)
    turtle.pendown()
    turtle.pensize(2)
    level = 4
    koch(400,level)
    turtle.right(120)
    koch(400,level)
    turtle.right(120)
    koch(400,level)
    turtle.hideturtle()
main()

14.作业

def drawsq(n):
    line=3*n+1#这相当于于循环打配合，搞定用户输入于行数的打印关系
    for i in range(1,line+1):
        if i%3 == 1:#当是第1，4，7...行时，打印的是横排连着的样式
            print(n*"+----",end="")#几阶便打印多少个
            print("+")
        else:
            print("|    "*n,end="")
            print("|")
def main():
    n=eval(input("请输入您要的阶数:"))
    drawsq(n)
main()

def isOdd(n):
    try:
        if n % 2 == 0:
            return False
        if type(n) == type(0.):#因为输入float并不会报错，当它并不属于我们的需要类型
            return False
        else:
            return True
    except:
        print("输入格式错误！")
print(isOdd(4))
print(isOdd(3))
print(isOdd(-1))
print(isOdd('str'))
print(isOdd(3.))
print(isOdd(str))
'''
False
True
True
输入格式错误！
None
False
输入格式错误！
None
'''

def isPrime(num):
    import math
    try:
        if type(num) == type(0.):
            raise TypeError#raise是保留字,手抛异常类型
        r = int(math.floor(math.sqrt(num)))#math.floor()向下取整；sqrt()计算平方根
    except TypeError:
        print('不是一个有效的整数')
        return None
    if num == 1:
        return False
    for i in range(2,r+1):
        if num % i == 0:#num逐步取余，为0则i为num的因数
            return False
    return True
#TypeError类型错误，将float也归于此类中，以此排除float、str的干扰
#num为1不符合素数定义
#for循环遍历判断是否为素数
print(isPrime(2))
print(isPrime(44))
print(isPrime('str'))
print(isPrime(1))
print(isPrime(3.3))
print(isPrime(0x18))
'''
素数：在大于1的自然数中，只有1和它本身两个因数
判断素数的平方根技巧
假设我们有一个整数 n，我们要判断它是否为素数。最直观的方法是检查从 2 到 n−1 的
所有整数是否能整除 n。如果没有任何一个数能整除 n，那么 n 就是素数。
但是， 对于较大的 n 来说非常低效.我们可以利用一个重要的数学性质来优化这个过程：
如果 n有一个大于根号n的因子，那么它必定有一个小于或等于根号n的因子。
因此，我们只需要检查从 2 到 根号n的所有整数即可。
如果n有一个大于 根号n的因子，那么它必定有一个小于或等于 根号n的因子。
因此，我们只需要检查从 2 到 根号n的所有整数即可。
'''

def PrimeList(N):
    def is_prime(num):
        if num <= 1:
            return False
        for i in range(2, int(num**0.5) + 1):
            if num % i == 0:
                return False
        return True
    primes = []
    for num in range(2, N):
        if is_prime(num):
            primes.append(num)#ls.append()向列表中加入元素
    return ' '.join(map(str, primes))#map(f,iters)它用于将函数功能f逐一作用于组合类型参数iters的各元素
N = eval(input("请输入N值:"))
print(PrimeList(N))
#line2~8是判断一个数是否为质数的函数

def isNum(s):
    try:
        # 尝试将字符串转换为复数类型
        complex(s)
        return True
    except ValueError:
        return False

def multi(i,*b):#可变参数b被当作元组类型遍历
    for n in b:
        i *= n
    return i
print(multi(1,3,4))

'''
def multi(*args):
    sum = 1
    count = 1
    for i in args:
        if type(i) is type(1) or type(i) is type(1.):#使用type(i) is type(1) 和 type(i) is type(1.) 来检查参数 i 是否为整数或浮点数
            sum *= i
        else:
            print("第{}项不是一个有效的整数！".format(count))
            return;
        count += 1
    return sum;
print(multi(2,3,1.0,5,4.99))
print(multi(2,1,'str'))
print(multi())
'''

def FabN(n):
    # 基本情况：当n为0或1时，直接返回n
    if n == 0:
        return 0
    elif n == 1:
        return 1
    # 递归情况：返回前两项的和
    else:
        return FabN(n-1) + FabN(n-2)
#不得不说递归是懵中带着神奇

def isType(value):
    if isinstance(value, int):
        return "整数"
    elif isinstance(value, float):
        return "小数"
    elif isinstance(value, complex):
        return "复数"
    elif isinstance(value, str):
        return "字符串"
    elif isinstance(value, list):
        return "列表"
    elif isinstance(value, dict):
        return "字典"
    elif isinstance(value, set):
        return "集合"
    elif isinstance(value, tuple):
        return "元组"
    else:
        return "未知类型"

# 示例使用
print(isType(123))        # 输出: 整数
print(isType(123.45))     # 输出: 小数
print(isType(1+2j))       # 输出: 复数
print(isType("hello"))    # 输出: 字符串
print(isType([1, 2, 3]))  # 输出: 列表
print(isType({"a": 1}))   # 输出: 字典
print(isType({1, 2, 3}))  # 输出: 集合
print(isType((1, 2, 3)))  # 输出: 元组
'''
isinstance() 是 Python 中的一个内置函数，用于检查一个对象是否属于指定的类型或其子类。
它的语法是 isinstance(object, classinfo)，
其中 object 是要检查的对象，classinfo 是要检查的类型或类型元组。
如果 object 是 classinfo 的实例或子类的实例，则返回 True，否则返回 False
'''

15.math 库

math库是Python标准库

from math import *
1.基本数学运算
sqrt(x)#计算x的平方根
pow(x,y)#计算x的y次方
floor(x)#向下取整
ceil(x)#向上取整
fabs(x)#返回x的绝对值
2.三角函数
sin()#计算x的正弦值
cos(x)#计算x的余弦值
tan(x)#计算x的正切值
asin(x)#计算x的反正弦
acos(x)#计算x的反余弦
atan(x)#计算x的反正切
3.对数和指数函数
math.log(x)：计算x的自然对数。
math.log10(x)：计算x的以10为底的对数。
math.exp(x)：计算e的x次方。
4.其他常用函数
math.pi：返回圆周率π的值。
math.e：返回自然对数的底e的值。
math.fmod(x, y)：返回x除以y的余数。
5.特殊函数
math.gamma(x)：计算x的伽玛函数。
math.erf(x)：计算x的误差函数。
math.erfc(x)：计算x的互补误差函数。
6.角度转换
math.degrees(x)：将弧度转换为角度。
math.radians(x)：将角度转换为弧度。
7.统计函数
math.factorial(x)：计算x的阶乘。
8.常量
math.inf：表示正无穷大。
math.nan：表示非数值（NaN）