7.25 7.26集训——初等数论

DL24zhanghao

已于 2022-08-05 09:28:02 修改

阅读量168

点赞数 5

分类专栏：数论文章标签：线性代数

于 2022-07-26 22:41:44 首次发布

本文链接：https://blog.csdn.net/DL24zhanghao/article/details/125984533

版权

数论专栏收录该内容

3 篇文章 0 订阅

订阅专栏

整除理论

素数定理

令 π(n) 为小于等于 n 的素数个数，有 π(n)=Θ(n/lnn)

算数基本定理

每个正整数都可以唯一的表示成质数的乘积，其中质数因子从小到大依次出现（这里的“乘积”可以有0个、1个或多个质因子）

素数判定

单点 O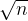（ $\sqrt{n}$ ）

for(int i=1;i<=sqrt(n);i++)
{
	if(n%i==0)
	{
		p[n]=0;
	}
} 
p[n]=1;

埃氏筛 O（nloglogn）

for(int i=2;i<=n;i++)
{
	p[i]=1;
}
for(int i=2;i<=n;i++)
{
	if(p[i])
	{
		for(int j=i*2;j<=n;j+=i)
		{
			p[j]=0;
		}
	}
}

线性筛 O（n）

for(int i=2;i<=n;i++)
{
	if(!vis[i])
	{
		p[++pn]=i;
	}
	for(int j=1;i*p[j]<=n;j++)
	{
		vis[i*p[j]]=1;
		if(i%p[j]==0)
		{
			break;
		}
	}
}

整除理论

对于整数a和b，若存在整数q使得aq=b，那么称a为b的约数，b是a的倍数，记作a|b

$a|b, b|c -> a|c$
$a|b,a|c->a|s\times b+t\times c$
$a|b,b|a->|a|=|b|$
设a和b是两个整数，如果 $d|a$ 且 $d|b$ ，则称d是a与b的公因子
设a和b是两个不全为0的整数，称a与b的公因子中最大的为a与b的最大公因子，或最大公约数，记作 $gcd(a,b)$ 或 $(a,b)$
设a和b是两个非零整数，称a与b的最小的正公倍数为a与b的最小公倍数，记作 $lcm(a,b)$ 或 $[a,b]$
若 $a|m,b|m$ , 则 $lcm(a,b)|m$
若 $d|a,d|b$ , 则 $d|gcd(a,b)$
$lcm(a,b)=\frac{ab}{gcd(a,b))}$
设m,a,b是正整数，则 $lcm(ma,mb)=m\times lcm(a,b),gcd(ma,mb)=m\times gcd(a,b)$

首先将a和b进行素因子分解成 $a=p_{1}^{r_{1}} p_{2}^{r_{2}}...p_{k}^{r_{k}},b=p_{1}^{s_{1}} p_{2}^{s_{2}}...p_{k}^{s_{k}}$
这里 $p_{1},p_{2},...,p_{k}$ 是不同的素数，则有
$gcd(a,b)=p_{1}^{min(r_{1},s_{1})} p_{2}^{min(r_{2},s_{2})}...p_{k}^{min(r_{k},s_{k})}$
$lcm(a,b)=p_{1}^{max(r_{1},s_{1})} p_{2}^{max(r_{2},s_{2})}...p_{k}^{max(r_{k},s_{k})}$

辗转相除法 O(log(a+b))

$(a,b)=(b,a%b)$

int gcd(int x,int y)
{
	return y==0?x:gcd(y,x%y);
}

同余理论

整数a,b满足 $m|a-b$ ，那么称a和b在模m下同余，记作 $a\equiv b (mod m)$
对于 $a\equiv b (mod m)$ ，若 $d|m$ ， $d|a$ ， $d|b$ ，则 $\frac{a}{d}\equiv \frac{b}{a}(mod \frac{m}{d})$
对于 $a\equiv b (mod m)$ ，有 $gcd(a,m)=gcd(b,m)$
对于质数m1和m2，若 $gcd(m1,m2)=1$ $gcd(m1,m2)=1$ ,则 $\left \{ m_{2}x_{1}+m_{1}x_{2}mod m_{1}m_{2}|x1,x2\epsilon \mathbb{Z} \right \}=\left \{x mod m_{1}m_{2}|x\epsilon \mathbb{Z} \right \}$

exgcd O(log(a+b))

求解线性不定方程 $ax+by=gcd(a,b)$

void exgcd(int a,int b,int &g,int &x,int &y)
{
	if(!b)
	{
		x=1,y=0,g=a;
	}
	else
	{
		exgcd(b,a%b,g,y,x);
		y-=x*(a/b);
	}
}

证明过程：

求 $ax+by=z$
$ax+by=gcd(a,b)->a(x*(z/gcd(a,b)))+b(y*(z/gcd(a,b)))=z$
可以看出有解的充要条件是 $gcd(a,b)|z$

乘法逆元

对于正整数a，若存在s使 $as=1(mod m)$
记s是a在模m下的逆元，即 $s=a^{-1}(mod m)$
a存在逆元的充要条件 $(a,m)=1$

费马小定理

若p是质数，则对于任意整数a有 $a^{p}=a(mod p)$

威尔逊定理

若p是质数，则有 $(p-1)!=-1(mod p)$

线性推逆元 O(n)

若 $ki+r=0(modm)$
$i^{-1}=-kr^{-1}(mod m)$ (m是质数)

inv[1]=1;
for(int i=2;i<=p;i++)
{
	inv[i]=(p-p/i)*inv[p%i]%p;	
}

a在模m下的乘法逆元

m是质数：费马小定理，线性推逆元
m不是质数：exgcd
$ax+bm=1$
$ax\equiv 1(mod m)$
$x\equiv a^{-1}(mod m)$

例题

给定n个数 $a_{1}...a_{n}$ ,求其在模p意义下的逆元，n<2e7，p<1e9，保证p为质数

设 $pre_{i}$ 为 $a_{1},a_{2},...,a_{i}$ 的前缀积（即 $pre_{i}=\prod_{j=1}^{i}a_{j}$ ）
$pre_{i}^{-1}=a_{i+1}\times pre_{i+1}^{-1}(1\leqslant i< n)$
$a_{j}^{-1}=pre_{j-1}\times pre_{j}^{-1}(1\leqslant j\leqslant n)$

中国剩余定理

对于n个同余方程 $x\equiv r_{i}(modm_{i})$ 形成的同余方程组，求最小的x，其中 $m_{i}$ 两两互质

设 $M=\prod_{n}^{i=1}m_{i}$ ， $M_{i}=\frac{M}{m_{i}}$ ， ${M}^{'}_{i}=M_{i}^{-1}(mod m_{i})$

则其解为 $x\equiv \sum_{i+1}^{n}r_{i}{M}^{'}_{i}M_{i}(mod M)$

扩展中国剩余定理

对于 n 个同余方程 x ≡r_i (mod m_i) 形成的同余方程组，求最小的 x。其中 m_i 不满足两两互质。
考虑已经求得前 j-1 个方程的解 R，前 j-1 个方程的模数的 lcm 是 M，现在则考虑 $x=R+MA$ , $x=r_j+m_jB$ ，联立用 exgcd 解 A 和 B 即可。
“扩展CRT”“扩展中国剩余定理”，其实就是⽤exgcd⼀个个合并这些同余⽅程。
以合并两个同余⽅程 $x \equiv b_{1} (mod m_{1})$ $x \equiv b_{2} (mod m_{2})$ 为例，⽅程组有解的充要条件是 $(m_{1},m_{2})|(b_{1}-b_{2})$ , 此时x在模 $[m_{1}, m_{2}]$ 意义下有唯⼀解。
该⽅程组等价于 $x = b_{1} + m_{1}y_{1}$ $x = b_{2} + m_{2}y_{2}$
则 $b_{1} - b_{2} = m_{2}y_{2} - m_{1}y_{1}$
exgcd求出 $y_{1}$ 、 $y_{2}$ ，可求出x在模 $[m_{1},m_{2}]$ 意义下的唯⼀解 $x =(b_{1} + m_{1}y_{1})% [m_{1}, m_{2}]$ 。

欧拉函数

⼀个数x的欧拉函数φ(x)为⼩于x的正整数中与x互质的数的个数
特别地，φ(1) = 1。
欧拉函数的一种求法： $\varphi (x)=x\coprod_{i=1}^{n}(1-\frac{1}{p_{i}})$ 其中 $p_{1}...p_{n}$ 是x的所有质因数。
欧拉函数的性质

积性函数！

积性函数：若对任意互质的两个数m和n有 $f(m\times n)=f(m)\times f(n)$ ，则 f(x)是积性函数。若对任意两个数（不要求互质）都有 $f(m\times n)=f(m)\times f(n)$ ，则f(x)是完全积性函数。

2.对质数p， $\varphi (p)=p-1$ 。

3. ⼩于n的数中，与n互质的数之和为 $\varphi (n) \times \frac{n}{2} (n>1)$ 。

4. n的所有因数的欧拉函数之和等于n

如何快速求欧拉函数
可以发现欧拉函数对乘法有很好的性质
$\varphi (n)=\left\{\begin{matrix}\varphi (\frac{n}{m})\times m (m|(\frac{n}{m})) \\ \varphi (\frac{n}{m})\times\varphi(m)(else) \end{matrix}\right.$
m为n最小的质因子
这启发我们用线性筛求欧拉函数

for(int i=2;i<=n;i++)
{
	if(!vis[i])
	{
		p[++pn]=i;
		phi[i]=i-;
	}
	for(int j=1;i*p[j]<=n;j++)
	{
		vis[i*p[j]]=1;
		if(i%p[j]==0)
		{
			phi[i*p[j]]=phi[i]*p[j];
			break;
		}
		phi[i*p[j]]=phi[i]*phi[p[j]];
	}
}

莫比乌斯函数

可以发现线性筛除了可以筛素数，还有别的应⽤——O(n)筛积性函数！
尝试：莫比乌斯函数μ(n)定义如下图，O(n)求1~n的莫比乌斯函数。
$\mu (n)=\left\{\begin{matrix}\, \, \, \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! 1 \;\;\;\;\;\;\;\;\;\;\; \;\! \! \! \! \! \! \! \! \! n=1 \\ (-1)^{k} \; \; \;\;\;\;\! \! \! \! \! n=p_{1}p_{2}...p{k} \\ \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! 0 \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! else \end{matrix}\right.$

//线性筛莫比乌斯函数
mu[1]=1;
for(int i=2;i<=n;i++)
{
	if(!vis[i])
	{
		p[++pn]=i;
		phi[i]=-1;	
	}	
	for(int j=1;i*p[j]<=n;j++)
	{
		vis[i*p[j]]=1;
		if(i%p[j]==0)
		{
			mu[i*p[j]]=0;
			break;
		}
		phi[i*p[j]]=-phi[i];
	}
}

定义函数d(x)为x的因数个数，O(n)求1~n的因数个数

//d[x]:x中的因数个数
//e[x]:x中最小质因数的次数
d[1]=1;
for(int i=2;i<=n;i++)
{
	if(!vis[i])
	{
		p[++pn]=i;
		d[i]=2;
		e[i]=1;	
	}	
	for(int j=1;j<=pn&&i*p[j]<=n;j++)
	{
		vis[i*p[j]]=1;
		if(i%p[j]==0)
		{
			e[i*p[j]]=e[i]+1;
			d[i*p[j]]=d[i]/(e[i]+1)*(e[i]+2);
			break;
		}
		else
		{
			e[i*p[j]]=1;
			d[i*p[j]]=d[i]*2;
		}
	}
}

欧拉定理

欧拉定理：若 m 是正整数， $gcd(a,m)=1$ ，则有 $a^{\varphi(m) }=1 (mod m)$
可以看出费马小定理是欧拉定理的特殊情况

证明：

扩展欧拉定理

若m,n是正整数， $n>\varphi (m)$ ,则有 $a^{n mod \varphi (m)+\varphi(m)}(mod m)$

Lucas定理

给定质数p，求 $\binom{n}{k}=\binom{n/p}{k/p}\binom{n%p}{k%p}$

相当于把n和k拆成p进制数，然后每一位对应求组合数，最后再乘起来

DL24zhanghao

关注

5
点赞
踩
0

收藏

觉得还不错? 一键收藏
0
评论
7.25 7.26集训——初等数论

整除理论素数定理算数基本定理素数判定单点 O（编辑）埃氏筛 O（nloglogn）线性筛 O（n）整除理论辗转相除法 O(log(a+b))同余理论 exgcd O(log(a+b))乘法逆元费马小定理威尔逊定理线性推逆元 O(n)a在模m下的乘法逆元例题中国剩余定理扩展中国剩余定理欧拉函数莫比乌斯函数欧拉定理扩展欧拉定理Lucas定理...
复制链接

扫一扫