递推算法

递推算法
 

“递推”是计算机解题的一种常用方法。利用“递推法”解题首先要分析归纳出“递推关系”。比如经典的斐波那契数列问题，用f(i)表示第i项的值，则f(1)=0,f(2)=1，在 n>2 时，存在递推关系：f(n)=f(n-1)+f(n-2)。
      
在递推问题模型中，每个数据项都与它前面的若干数据项(或后面的若干数据项)存在一定的关联，这种关联一般是通过一个“递推关系式”来描述的。求解问题时，需要从初始的一个或若干数据项出发，通过递推关系式逐步推进，从而推导计算出最终结果。这种求解问题的方法叫“递推法”。其中，初始的若干数据项称为“递推边界”。
      
解决递推问题有三个重点：一是建立正确的递推关系式；二是分析递推关系式的性质；三是根据递推关系式编程求解。
      
根据推导问题的方向,递推法分为“顺推”和“倒推”两类模型。所谓顺推，就是从问题的边界条件(初始状态)出发，通过递推关系式依次从前往后递推出问题的解；所谓倒推，就是在不知道问题的边界条件(初始状态)下，从问题的最终解(目标状态或某个中间状态)出发，反过来推导问题的初始状态。

例1.斐波那契数列。

     
满足F1 = F2 = 1, Fn = Fn-1 + Fn-2的数列称为斐波那契数列（Fibonacci），它的前若干项是1 , 1 , 2 , 3 , 5 , 8, 13 , 21 , 34……求此数列第n项（n>=3）。

即f1=1                         (n=1)

   f2=1                         (n=2)

   fn=fn-1+fn-2           (n>=3)

程序如下：
//非数组解法

#include<iostream>
using namespace std; 
int main(){
	int f0=1, f1=1, f2;
	int n;
	cin>>n;
	for(int i=3; i<=n; i++){
		f2=f0+f1;
		f0=f1;
		f1=f2;
	}
	cout<<f2;
}

//数组解法
#include<iostream>
using namespace std; 
int main(){
	int f[1005];
	int n;
	cin>>n;
	f[1]=1; f[2]=1;
	for(int i=3; i<=n; i++){
		f[i]=f[i-1]+f[i-2];
	}
	cout<<f[n];
	return 0;
}

（1）.楼梯有n个台阶，上楼可以一步一阶，也可以一步两阶。一共有多少中上楼的方法？

这是一道计数问题。在没有思路时，不妨试着找规律。n=5时，一共有8种方法：
5=1+1+1+1+1
5=2+1+1+1
5=1+2+1+1
5=1+1+2+1
5=1+1+1+2
5=2+2+1
5=2+1+2
5=1+2+2
其中有5种方法第一步走了1阶，3种方法第一步走了2阶，没有其他可能。假设f(n)为n个台阶的走法总数，把n个台阶的走法分成两类。
第一类：第一步走了1阶，剩下还有n-1阶要走，有f(n-1)种方法。
第一类：第一步走了2阶，剩下还有n-2阶要走，有f(n-2)种方法。
这样，就得到了递推式：f(n)=f(n-1)+f(n-2)，不要忘记边界情况 ： f(1)=1, f(2)=2。把f(n)的前n项列出：1,2,3,5,8......。

（2）.把雌雄各一的一对新兔子放入养殖场中。每只雌兔在出生两个月以后，每月产雌雄各一的一对新兔子。试问第n个月后养殖场中共有多少对兔子？
      还是先找规律：
     

 

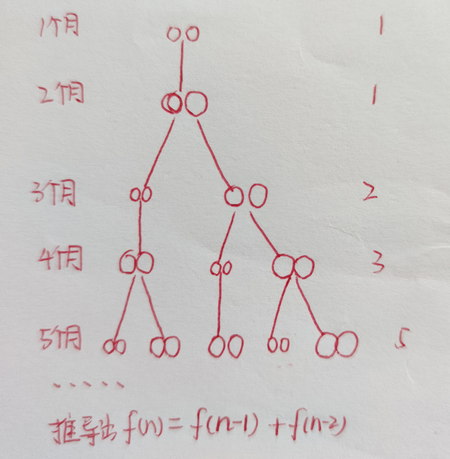
例2.铺瓷砖。

     
不同的铺设方案。用红色的 1×1和黑色的2×2 两种规格的瓷砖不重叠地铺满nx3的路面，求出有多少种不同的铺设方案。

【输入格式】

一行一个整数，0<n<1000。

【输出格式】

一行一个整数，为铺设方案的数量模12345上午结果。

【输入样例】

  2

【输入样例】

  3


 

【问题分析】
用f(n)表示 m x 3 的路面有多少种不同的铺设方案。把路面看成 n行3列，则问题可以分成两种情况考虑，一种是最后一行用 3块 1×1 的瓷砖铺设;另一种是最后两行用
1块 2x2 和2块 1×1 的瓷砖铺设(最后两行就有两种铺法)，第一种铺法就转换为f(i-1)的问题了，第二种铺法就转换成f(-2)的问题了。根据加法原理，得到的递推关系式为 
f(i)= f(i-1)+f(i-2)×2，边界为f(0)=1，f(1)=1。

程序如下： 

#include<iostream>
using namespace std; 

int main(){
	int n,a[100];
	cin>>n;
	a[0]=1; a[1]=1; 
	for(int i=2; i<=n; i++)
		a[i]=(a[i-1]+a[i-2]*2) % 12345;
	cout<<a[n];

例3.昆虫繁殖。

     
科学家在热带森林中发现了一种特殊的昆虫，这种昆虫的繁殖能力很强。每对成虫过x个月产y对卵，每对卵要过两个月长成成虫。假设每个成虫不死，第一个月只有一对成虫，且卵长成成虫后的第一个月不产卵（过x个月产卵〉，问过z个月以后，共有成虫多少对？O<= x<=20, l<=y<=20, x< =z< =50

【输入格式】
  
x,y,z 的数值。

【输出格式】
  
过z个月以后，共有成虫对数。

【输入样例】
  
1 2 8

【输入样例】
  
37

程序如下：

#include<iostream>
using namespace std; 
int main(){
	int a[105]={0}, b[105]={0}, x, y, z;
	cin>>x>>y>>z;
	
	for(int i=1; i<=x; i++){
		a[i]=1;   //a[i]是第i个月的成虫 
		b[i]=0;   //b[i]是第i个月的卵 
	}
	
	for(int i=x+1; i<=z+1; i++){   //因为要统计到第z个月后，所以要for到z+1 
		b[i]=a[i-x]*y;           //第i-x个月的成虫在x个月后产下y个卵 
		a[i]=a[i-1]+b[i-2];    //第i个月的成虫=第i-1个月的成虫数+第i-2个月的卵 
	} 
	cout<<a[z+1];
	return 0;
}

 

例4.位数问题。

     
在所有的n位数中，有多少个数中有偶数个数字 3？ 由于结果可能很大，你只需要输出这个答案对 12345 取余的值。

【输入格式】
  
读入一个数n。（1<=n<=1000）

【输出格式】
  
输出有多少个数中有偶数个数字3。

【输入样例】
  
2

【输入样例】
  
73

【样例说明】
  
在所有的 2位数字中，包含0个3的数有72个，包含2个3的数有1个，共73个。

【分析】考虑这种题目，一般来说都是从第i-l位推导第i位，且当前位是取偶数应是取奇数的。
    可以用a[i]表示前i位取偶数个3的情况，b[i]表示前i位取奇数个3的情况。
    n       a[i]                 b[i]
    1        9                    1      //124567890   3
    2      9*9+1*1=82          9*1+1*9=18      //a[i]:个位数0个3的可以和9个数结合 + 3可以和3结合。  b[i]：个位数0个3的可以和3结合 + 3可以和9个数结合。
    3     82*9+18*1=756        82*1+18*9=244       
    i     a[i-1]*9+b[i-1]     a[i-1]*1+b[i-1]*9
    ...
    n     a[n-1]*8+b[n-1]     a[n-1]*1+b[n-1]*8
    
    ①当位数是1的时候，有9个符合条件的（0个3也是含偶数个3），只有1个数字3不符合。
    ②当位数是2的时候，0~9（除了3）可以和0~9（除了3）结合成偶数个3，且3可以和3组合成偶数个3； 
    3可以和0~9（除了3）结合成奇数个3，且0~9（除了3）可以和3结合成奇数个3。
    ...
    ③因为012不构成三位数，也就是说第N位（最后一位的时候），不能把0算进去，
    所以要把*9变成*8。前n位时可以把0算进去，如x01 x02  xx09...


   

 【程序如下】：

 #include<iostream>
    using namespace std;
    int a[1005];     //偶数个3 
    int b[1005];     //奇数个3 
    int main()
    {
        int n, nums;
        cin>>n;
        
        //递推初值 
        a[1]=9;
        b[1]=1;
        nums=9;
        for(int i=2; i<=n; i++)
        {
        	if(i==n)
                nums=8;
            a[i]=(a[i-1]*nums + b[i-1]*1) % 12345;
            b[i]=(a[i-1]*1 + b[i-1]*nums) % 12345; 
        }
        cout<<a[n]<<endl;
        return 0; 
    }

 

五种典型的递推关系

---

• 1. Fibonacci数列
       
  Fibonacci数列的代表问题是由意大利著名数学家Fibonacci于1202年提出的“兔子繁殖问题” （又称 “Fibonacci问题”）。
       
  问题的提出：有雌雄一对兔子，假定过两个月便可繁殖雌雄各一的一对小兔子。问过n个月后共有多少对兔子？
       
  解：设满x个月共有兔子F[x]对，其中当月新生的兔子数目为N[x]对。第x-1个月留下的兔子数目设为F[x-1]对。 则：
       
  F[x]=N[x]+F[x-1]
       
  N[x]=F[x-2]       （即第X2个月的所有兔子到第x个月都有繁殖能力了）
  
  => F[x]=F[x-1]+F[x-2]       边界条件：F[0]=0, F[1]=1
  
       
  由上面的递推关系可依次得到
  
  F[2]=F[1]+F[0]=1, F[3]=F[2]+F[1]=2, F[4]=F[3]+F[2]=3, F[5]=F[4]+F[3]=5,... …
  
       
  Fabonacci数列常出现在比较简单的组合计数问题中，例如以前的竞赛中出现的“骨牌覆盖”问题。在优选法中，Fibonacci数列的用处也得到了较好的体现。

 

• 2. Hanoi塔问题
  
  问题的提出：Hanoi塔由n个大小不同的圆盘和l三根木柱a、b、c组成。开始时，这n个团盘由大到小依次套在a柱上，如图所示。
       
  要求把a柱上n个圆盘按下述规则移到c柱上：
  
   

  

  
       
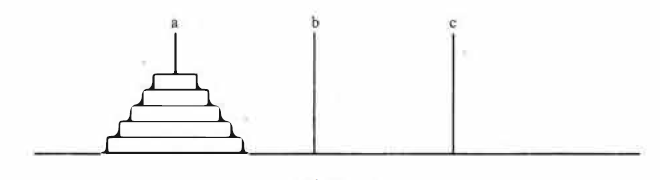
  (1）一次只能移一个圆盘；
       
  (2）圆盘只能在三个柱上存放；
       
  (3）在移动过程中，不允许大盘压小盘。
       
  问将这n个盘子从a柱移动到c柱上，总计需要移动多少个盘次？

  解：设h[n]为n个盘子从a柱移到c柱所需移动的盘次。显然，当n=l时，只需把a柱上的盘子直接移动到c柱就可以了，故h[1]=l。当n=2时，先向a柱上面的小盘子移动到
  

  b柱上去；然后将大盘子从柱移到c柱；最后，将b柱上的小盘子移到c柱上，共记3个盘次，故 h2=3。以此类推，当a柱上有n(n>=2）个盘子时，总是先借助c柱把上面的n-1个
  盘子移动到b柱上，然后把a柱最下面的盘子移动到c柱上；再借助a柱把b 柱上的n-1个盘子移动到c柱土；总共移动h[n-1]+1+h[n-1]

  所以h[n]=2*h[n-1]+1      边界条件：h[1]=1
  

 

• 3. 平面分割问题
       
  问题的提出：设有n条封闭曲线画在平面上，而任何两条封闭曲线恰好相交于两点，且任何三条封闭曲线不相交于同一点，问这些封闭曲线把平面分割成的区域个数。
   

  

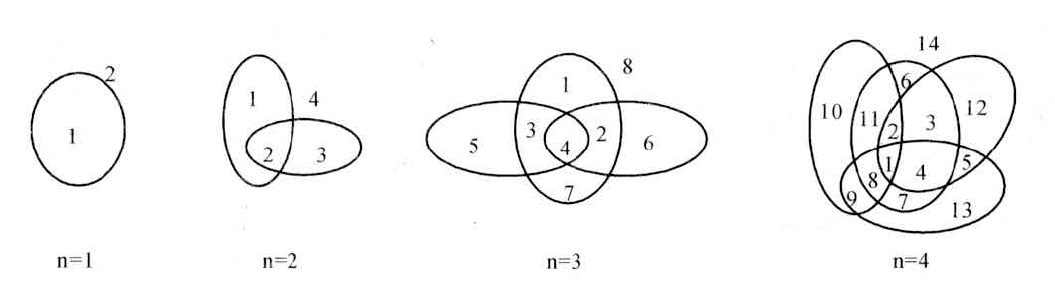
  解：设a[n]为n条封闭曲线把平面分割成的区域个数。由图可以看出：a[2]-a[1] = 2; a[3]-a[2] = 4; a[4]-a[3] = 6;
  
  从这些式子中可以看出a[n] - a[n-1] = 2(n-1)。下面来验证：
  
  当平面上已有n-1条曲线将平面分割成a[n-1]个区域后，第n-1条曲线每与曲线相交一次．就会增加一个区域，因为平面上已有了n-1条封闭曲线，且第n条曲线与已有的每一条
  闭曲线恰好相交于两点．且不会与任两条曲线交于同一点，故平面上一共增加2(n-1)个区域，加上已有的a[n-1]个区域，一共有a[n-1] +2(n-1)个区域。 所以本题的递推
  关系是a[n] = a[n-1] + 2(n-1)，边界条件是a1 = 1。
  

平面分割问题是竞赛中经常触及到的一类问题，由于其灵活多变，常常感到棘手。

 

• 4. Catalan数

 

• 5. 第二类Stirling数
       
  在五类典型的递推关系中，第二类Stirling是最不为大家所熟悉的。 也正因为如此，我们有必要先解释一下什么是第二类Stirling数。
       
  【定义】 n个有区别的球放到m个相同的盒子中，要求无一空盒，其不同的方案数用 S(n, m)表示，称为第二类Stirling数。
       
  下面就让我们根据定义来推导带两个参数的递推关系————第二类Stirling数。

    解：设有n个不同的球，分别用b1，b2， … ，bn表示。 从中取出一个球bn，bn的放法有以下两种：
    
    ① bn 独向占一个盒子；那么剩下的球只能放在m-1个盒子中，方案数为S(n-1, m-1)；
    ② bn 与别的球共占一个盒子；那么可以事先将 b1，b2， … ，bn-1 这n-1个球放入m个盒子中，然后再将球bn放入其中一个盒子中，方案数为m*S(n-1,m）。
    
    综合以上两种情况，可以得出第二类Stirling数定理：
    S(n,m) = m*S(n-1, m) + S(n-1, m-1)   ( n>l , m>=1 )
    
    边界条件可以由定义推导出：
    S(n,0)=0;   S(n,1)=1;   S(n,n)=1;   S(n,k)=0   ( k> n）。
    
    第二类Stirling数在竞赛中较少出现，但在竞赛中也有一些题目与其类似，甚至更为复杂。 
    小结：通过上面对五种典型的递推关系建立过程的探讨．可知对待递推类的题目，要具体情况具体分析，通过找到某状态与其前面状态的联系，建立相应的递推关系。