Math Reference Notes: 绝对值

绝对值（Absolute Value） 是数学中的一个基本概念，它用来表示一个数到零的距离。绝对值与数的符号无关，只关心数的大小。因此，绝对值是一个非负数，表示数在数轴上与原点（零点）的距离。

---

1. 绝对值的定义

绝对值记作 $|x|$，对于任意实数 $x$，定义如下：

$$|x|=\{\begin{array}{ll}x,& \text{如果 }x\ge 0\\ -x,& \text{如果 }x<0\end{array}$$

这意味着：

• 当 $x$ 是正数或零时，绝对值等于 $x$ 本身。
• 当 $x$ 是负数时，绝对值等于 $x$ 的相反数（即 $-x$），使得绝对值结果始终为正。

2. 绝对值的几何意义

在几何中，绝对值可以解释为距离的概念。对于一维空间（数轴），绝对值表示的是一个数与零点的距离。在二维或三维空间中，绝对值通常与距离的计算有关。

• 一维数轴：
  在一维数轴上，绝对值 $|x|$ 表示点 $x$ 到零点（原点）的距离。例如，点 $x=-3$ 到原点的距离是 3，点 $x=3$ 到原点的距离也是 3。

• 二维空间中的绝对值：
  在平面直角坐标系中，绝对值常常出现在距离公式中。例如，两个点 $(x_1,y_1)$ 和 $(x_2,y_2)$ 之间的距离公式为：
  $$d=\sqrt{(x_2-x_1{)}^2+(y_2-y_1{)}^2}$$
  这里的每个差值都会平方，因此不会有负数。这个公式的每部分差值和绝对值的运用是一样的，表示两个点在每一维上的“差距”。

3. 绝对值的性质

1. 非负性 (Non-negativity)

   绝对值的定义表明，它总是非负的，也就是说任何数的绝对值都不小于零。
   数学表达式为：
   $$|x|\ge 0\text{对于所有实数 }x$$
   这表示无论 $x$ 是正数、负数还是零，绝对值始终是零或正数。例如：

   • $|3|=3$
   • $|-5|=5$
   • $|0|=0$

2. 自反性 (Reflexivity)

   绝对值等于零当且仅当该数本身为零。这一性质表明，只有零的绝对值为零，任何其他数的绝对值都不可能为零。
   数学表达式为：
   $$|x|=0\text{当且仅当}x=0$$
   例如：

   • 如果 $x=0$，那么 $|0|=0$。
   • 如果 $x=3$ 或 $x=-3$，则 $|x|=3\ne 0$。

3. 对称性 (Symmetry)

   绝对值忽略了数的符号，因此 $x$ 和 $-x$ 的绝对值相等。无论是正数还是负数，绝对值是相同的。
   数学表达式为：
   $$|x|=|-x|$$
   例如：

   • $|5|=|-5|=5$
   • $|7.2|=|-7.2|=7.2$

4. 三角不等式 (Triangle Inequality)

   绝对值满足三角不等式，这意味着对于任意两个数 $x$ 和 $y$，它们和的绝对值不超过各自绝对值的和。
   数学表达式为：
   $$|x+y|\le |x|+|y|$$
   该性质的几何解释是，在数轴上，一个数从 $x$ 移动到 $y$ 的绝对值距离不会超过分别从 $x$ 到 $0$ 和从 $0$ 到 $y$ 的绝对值距离的和。
   例如：

   • 如果 $x=3$，$y=-2$，那么 $|3+(-2)|=|1|=1\le |3|+|-2|=3+2=5$。

5. 乘法性 (Multiplication Property)

   绝对值运算与乘法具有分配性，即两个数的乘积的绝对值等于它们各自绝对值的乘积。
   数学表达式为：
   $$|xy|=|x|\cdot |y|$$
   这一性质在简化乘法中的绝对值运算时非常有用。例如：

   • $|2\cdot (-3)|=|2|\cdot |-3|=2\cdot 3=6$。

6. 除法性 (Division Property)

   对于两个数的商，绝对值的性质表明，只要分母不为零，商的绝对值等于分子和分母绝对值的商。
   数学表达式为：
   $$\left|\frac{x}{y}\right|=\frac{|x|}{|y|}\text{当 }y\ne 0$$
   例如：

   • $\left|\frac{6}{-2}\right|=\frac{|6|}{|-2|}=\frac{6}{2}=3$。

4. 绝对值函数的图像

绝对值函数 $y=|x|$ 是一种常见的数学函数，其图像具有以下显著特点：

图像基本特征

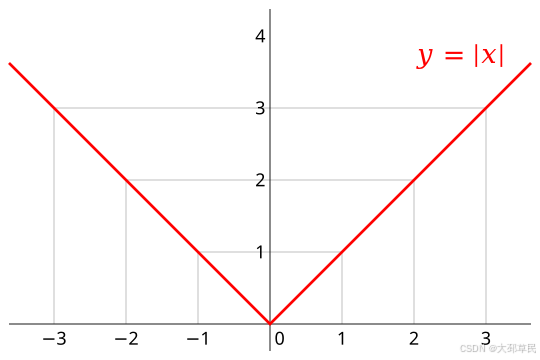
• V字形：绝对值函数的图像呈现 “V” 字形，表示对于每个 $x$，函数值 $y=|x|$ 只取非负值，无论 $x$ 是正数还是负数。也就是说，$y$ 始终大于或等于零。
• 原点处的尖点：在 $x=0$ 处，绝对值函数的图像有一个尖点，因为函数在该点的左右导数不相等。其图像在 $x=0$ 处不可导。
• 右侧上升：当 $x\ge 0$ 时，绝对值函数的图像是 $y=x$，即图像为一条通过原点、斜率为 1 的直线。
• 左侧下降：当 $x<0$ 时，图像是 $y=-x$，即图像为一条通过原点、斜率为 -1 的直线。

整体来看，绝对值函数的图像在原点形成一个尖角，并且关于 $y$-轴对称。

5. 绝对值的拓展

• 欧几里得距离（二维及高维空间）

  绝对值不仅限于一维，它也可以在更高维空间中进行拓展。

  • 二维空间中的绝对值：对于平面上的点 $(x,y)$，其到原点 $(0,0)$ 的距离定义为欧几里得距离，公式如下：
    $$|(x,y)|=\sqrt{x^2+y^2}$$
    这个表达式给出了点 $(x,y)$ 到原点 $(0,0)$ 的直线距离。它是一种常见的距离度量，广泛用于物理学、计算机图形学等领域。

  • 三维及高维空间中的绝对值：对于 $n$ 维空间中的点 $(x_1,x_2,\dots ,x_n)$，到原点的距离可以表示为：
    $$|(x_1,x_2,\dots ,x_n)|=\sqrt{x_1^2+x_2^2+\cdots +x_n^2}$$
    这就是 $n$ 维欧几里得空间中的距离度量。其物理意义是点 $(x_1,x_2,\dots ,x_n)$ 与原点 $(0,0,\dots ,0)$ 的直线距离。

• 曼哈顿距离（城市街区距离）

  曼哈顿距离（又称城市街区距离）用于计算在格状道路网格中，两个点之间的距离。它是通过在水平和垂直方向上沿街道行走的距离来度量的。对于两个点 $(x_1,y_1)$ 和 $(x_2,y_2)$，曼哈顿距离计算公式为：
  $$d(x_1,y_1,x_2,y_2)=|x_1-x_2|+|y_1-y_2|$$
  这种距离度量方式通常用于城市规划、物流优化等领域。

6. 绝对值的应用

1. 几何应用

   绝对值在几何学中的应用广泛，特别是在计算距离时：

   • 一维距离：在数轴上，两个点 $A(a)$ 和 $B(b)$ 之间的距离可以通过它们的差的绝对值来表示：
     $$\text{距离}=|a-b|$$

   • 欧几里得空间中的距离：在二维或三维空间中，点与点之间的距离同样使用绝对值表示。例如，二维平面上的两点 $(x_1,y_1)$ 和 $(x_2,y_2)$ 之间的距离为：
     $$d=\sqrt{(x_1-x_2{)}^2+(y_1-y_2{)}^2}$$

2. 物理学中的应用

   绝对值在物理学中常用于表示量的大小，特别是在不考虑方向时：

   • 速度和加速度：速度和加速度是典型的大小不依赖方向的量，因此常用绝对值表示其大小。例如，物体的速率为 $|v(t)|$，其中 $v(t)$ 是速度的时间函数。
   • 力和位移：力的大小、位移的大小等也使用绝对值。例如，位移的大小为 $|d|$，表示物体从一个点移动到另一个点的距离，而不考虑其方向。

3. 解方程

   绝对值广泛应用于解方程时：

   • 例如解方程 $|x|=5$ 时，有两个解：$x=5$ 或 $x=-5$。
   • 对于含有绝对值的方程，通常需要分情况讨论。例如，解方程 $|x-3|=5$，得到两个子方程：
     $$x-3=5\text{或}x-3=-5$$
     由此得出 $x=8$ 或 $x=-2$。

4. 优化问题

   在优化问题中，绝对值常用于构造约束条件或目标函数。例如，在最小化目标函数时，常常需要处理绝对值：

   • 例如，目标函数 $f(x)=|x-a|$ 的最小化表示寻找点 $x$ 与某个固定点 $a$ 之间的最小距离。最小值显然出现在 $x=a$ 时。

5. 不等式的证明

   绝对值广泛应用于不等式的证明中，尤其是在分析函数的单调性、极值等问题时。比如，解不等式 $|x-3|<5$ 时，我们可以得到：
   $$-5<x-3<5\Rightarrow -2<x<8$$
   这表明 $x$ 的取值范围为 $(-2,8)$。

6. 信号与控制系统

   在信号处理和控制系统中，绝对值常用于表示信号的幅度。例如，在控制系统中，系统的误差常用绝对值表示，误差函数可以表示为：
   $$E(t)=|y(t)-y_{\text{target}}|$$
   其中 $y(t)$ 是系统输出，$y_{\text{target}}$ 是目标值，$E(t)$ 是系统的误差。

7. 绝对值的扩展到复数域

在复数域中，绝对值的定义稍有不同。对于复数 $z=a+bi$，其中 $a$ 和 $b$ 是实数，$i$ 是虚数单位，复数 $z$ 的绝对值（模）定义为：
$$|z|=\sqrt{a^2+b^2}$$
这个定义与平面直角坐标系中点到原点的距离公式相同。几何上，复数的绝对值表示复数在复平面上到原点的距离。

复数的几何意义

在复数平面中，复数 $z=a+bi$ 可以表示为平面上的一个点 $(a,b)$，其绝对值 $|z|$ 就是该点到原点 $(0,0)$ 的欧几里得距离。通过这种方式，复数的绝对值与其在复平面上的位置密切相关。