poj2481 Cows 树状数组 解题报告

Cows
Time Limit: 3000MS Memory Limit: 65536K
Total Submissions: 15519 Accepted: 5182
Description
Farmer John’s cows have discovered that the clover growing along the ridge of the hill (which we can think of as a one-dimensional number line) in his field is particularly good.

Farmer John has N cows (we number the cows from 1 to N). Each of Farmer John’s N cows has a range of clover that she particularly likes (these ranges might overlap). The ranges are defined by a closed interval [S,E].

But some cows are strong and some are weak. Given two cows: cowi and cowj, their favourite clover range is [Si, Ei] and [Sj, Ej]. If Si <= Sj and Ej <= Ei and Ei - Si > Ej - Sj, we say that cowi is stronger than cowj.

For each cow, how many cows are stronger than her? Farmer John needs your help!
Input
The input contains multiple test cases.
For each test case, the first line is an integer N (1 <= N <= 105), which is the number of cows. Then come N lines, the i-th of which contains two integers: S and E(0 <= S < E <= 105) specifying the start end location respectively of a range preferred by some cow. Locations are given as distance from the start of the ridge.

The end of the input contains a single 0.
Output
For each test case, output one line containing n space-separated integers, the i-th of which specifying the number of cows that are stronger than cowi.
Sample Input
3
1 2
0 3
3 4
0
Sample Output
1 0 0
Hint
Huge input and output,scanf and printf is recommended.
Source
POJ Contest,Author:Mathematica@ZSU

本题还是看别人的代码才懂的，看了之后，懂的不仅仅是题解，而是道理：
问题要考虑2个变量时，可以先控制其中一个变量，考虑另一个变量。
就像这题，求第i个牛有多少个比它强的牛，需要考虑起点和终点。同时考虑没思路，那么可以先控制(排序)起点(终点),最后考虑终点(起点)。
假设考虑对起点升序（相等时对终点升序）:从左到右，依次添加牛的终点，这样后添加进来的牛的起点一定不必前面的小，所以对第j个牛，j>i，S[i]<=S[j],只需要考虑终点，即：终点大于E[j]的牛有多少个。那么问题就转化为：维护区间终点的个数（不断添加新的终点，不断访问某个区间有多少个终点）。

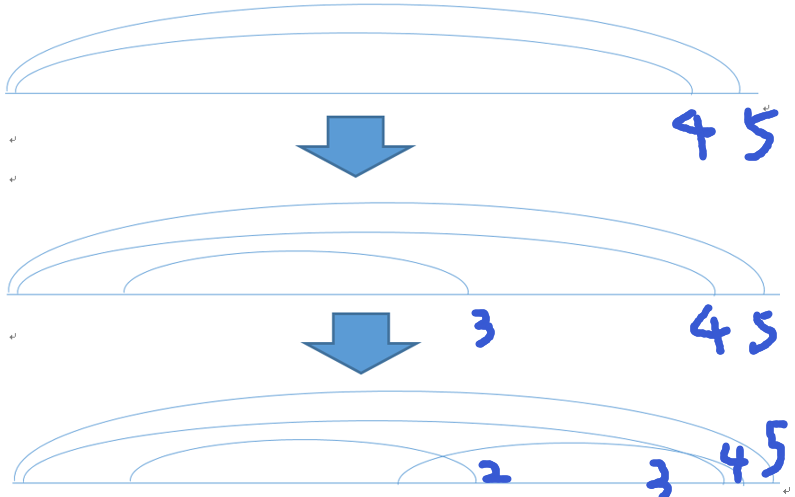
问题：线段树维护的是从0到该点的总和，而终点是递增的，所以题目要求从该点向后到终点的总和。
因此，考虑按终点降序，相等时按起点升序。同样从左到右一次添加起点和终点，后添加进来的牛的终点一定不大于前面的，所以只需要考虑起点，即：起点小于该牛起点的牛一共有多少个。这就符合线段树的求和特点。

#include <iostream>
#include <string.h>
#include<stdio.h>
#include<algorithm>
using namespace std;
const int MAXN=100005;
int n,maxnum;
int tree[MAXN];
int ans[MAXN];
struct Node{
    int s,e,id;
}node[MAXN];
bool cmp(Node a,Node b){
    if(a.e==b.e) return a.s<b.s;
    return a.e>b.e;
}
int getSum(int idx){
    int sum=0;
    while(idx>0){
        sum+=tree[idx];
        idx-=(idx&-idx);
    }
    return sum;
}
void update(int idx){
    while(idx<=maxnum+1){
        tree[idx]+=1;
        idx+=(idx&-idx) ;
    }
}
int main(){
    freopen("i.txt","r",stdin);
    while(scanf("%d",&n)&&n){
        maxnum=-1;//起点最小值 
        for(int i=0;i<=n;i++)ans[i]=0,tree[i]=0;
        for(int i=1;i<=n;i++){
            scanf("%d %d",&node[i].s,&node[i].e);
            node[i].id=i,node[i].s++,node[i].e++;
            if(maxnum<node[i].s)maxnum=node[i].s;
        }
        sort(node+1,node+n+1,cmp);
        ans[node[1].id]=getSum(node[1].s);
        update(node[1].s);
        for(int i=2;i<=n;i++){
            if(node[i].e==node[i-1].e&&node[i].s==node[i-1].s)
                ans[node[i].id]=ans[node[i-1].id]; 
            else ans[node[i].id]=getSum(node[i].s);//区间访问 
        update(node[i].s);//向区间添加起点 
        }
        cout<<ans[1];
        for(int i=2;i<=n;i++)printf(" %d",ans[i]);
        cout<<endl; 
    }
    return 0;
}