数字三角形模型
摘花生
graph LR;
id1((动态规划)) --> 状态表示 --f[i,j] --> 集合 --> 所有从1,1走到i,j的路线
状态表示 --> 属性 --> MAX
id1((动态规划)) --> 状态计算
状态计算:集合的划分。(很重要的划分依据:“最后”)
集合划分依据:1.不重复(但并不是所有情况都要满足) 2.不漏
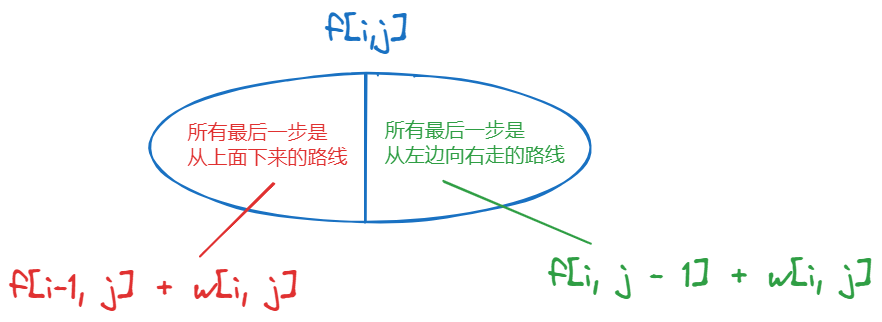
从 ( 1 , 1 ) (1,1) (1,1) 走到 ( i , j ) (i, j) (i,j) 的所有路线的最大值也就是 f ( n , m ) f(n, m) f(n,m)
f [ i , j ] = m a x ( f [ i − 1 , j ] , f [ i , j − 1 ] ) + w [ i , j ] f[i, j] = max(f[i - 1, j], f[i, j - 1]) + w[i, j] f[i,j]=max(f[i−1,j],f[i,j−1])+w[i,j]
#include<bits/stdc++.h>
using namespace std;
const int N = 1e3 + 50;
int f[N][N];
int w[N][N];
int t;
int main()
{
cin >> t;
while(t --)
{
int r, c;
cin >> r >> c;
for(int i = 1; i <= r; i ++)
for(int j = 1; j <= c; j ++)
cin >> w[i][j];
for(int i = 1; i <= r; i ++)
for(int j = 1; j <= c; j ++)
f[i][j] = max(f[i - 1][j], f[i][j - 1]) + w[i][j];
cout << f[r][c] << endl;
}
return 0;
}
最低通行费
原题链接
从 “商人必须在 (2N−1) 个单位时间穿越出去。” 得出不能走回头路。
本质上和摘花生这题差不多
#include<bits/stdc++.h>
using namespace std;
const int N = 150, INF = 1e9;
int w[N][N], f[N][N];
int n;
int main()
{
cin >> n;
for(int i = 1; i <= n; i ++)
for(int j = 1; j <= n; j ++)
cin >> w[i][j];
for(int i = 1; i <= n; i ++)
for(int j = 1; j <= n; j ++)
{
if(i == 1 && j == 1)
f[i][j] = w[i][j];
else
{
f[i][j] = INF;
if(i > 1)
f[i][j] = min(f[i][j], f[i - 1][j] + w[i][j]);
if(j > 1)
f[i][j] = min(f[i][j], f[i][j - 1] + w[i][j]);
}
}
cout << f[n][n] << endl;
return 0;
}
#include<bits/stdc++.h>
using namespace std;
const int N = 150, INF = 1e9;
int w[N][N], f[N][N];
int n;
int main()
{
cin >> n;
for(int i = 1; i <= n; i ++)
for(int j = 1; j <= n; j ++)
cin >> w[i][j];
memset(f, 0x3f, sizeof f);
f[1][1] = w[1][1];
for(int i = 1; i <= n; i ++)
for(int j = 1; j <= n; j ++)
{
f[i][j] = min(f[i][j], f[i - 1][j] + w[i][j]);
f[i][j] = min(f[i][j], f[i][j - 1] + w[i][j]);
}
cout << f[n][n] << endl;
return 0;
}
[NOIP2000 提高组] 方格取数
graph LR;
id1((动态规划)) --> 状态表示 --f[i1,j1,i2,j2] --> 集合 --> 所有从1,1与1,1分别走到i1,j1和i2,j2的路径
状态表示 --> 属性 --> MAX
id1((动态规划)) --> 状态计算
同一个格子不能被重复选择。
只有在 i1 + j1 == i2 + j2 时,两条路径的格子才可能重合。
状态表示可以优化为:f[k, i1, i2] 表示所有从 (1, 1), (1, 1) 分别走到 (i1, k - i1), (i2, k - i2) 的路径的最大值。
graph LR;
id1((动态规划)) --> 状态表示 --f[k, i1, i2] --> 集合 --> 所有从1,1和1,1分别走到i1,k-i1和i2,k-i2的路径
状态表示 --> 属性 --> MAX
id1((动态规划)) --> 状态计算
 第一种情况: 第一条从 $(1, 1) -> (i_1 - 1, j_1) -> (i_1, j_1)$, 第二条从 $(1, 1) -> (i_2 - 1, j_2) -> (i_2, j_2)$ $f[k, i_1, i_2] = max(f[k, i_1, i_2], f[k - 1, i_1-1, i_2-1] + tmp)$ 第二种情况: 第一条从 $(1, 1) -> (i_1 - 1, j_1) -> (i_1, j_1)$, 第二条从 $(1, 1) -> (i_2, j_2 - 1) -> (i_2, j_2)$ $f[k, i_1, i_2] = max(f[k, i_1, i_2], f[k - 1, i_1-1, i_2] + tmp)$ 第三种情况: 第一条从 $(1, 1) -> (i_1, j_1 - 1) -> (i_1, j_1)$, 第二条从 $(1, 1) -> (i_2 - 1, j_2) -> (i_2, j_2)$ $f[k, i_1, i_2] = max(f[k, i_1, i_2], f[k - 1, i_1, i_2-1] + tmp)$ 第四种情况: 第一条从 $(1, 1) -> (i_1, j_1 - 1) -> (i_1, j_1)$, 第二条从 $(1, 1) -> (i_2, j_2 - 1) -> (i_2, j_2)$ $f[k, i_1, i_2] = max(f[k, i_1, i_2], f[k - 1, i_1, i_2] + tmp)$
第一种情况: 第一条从 $(1, 1) -> (i_1 - 1, j_1) -> (i_1, j_1)$, 第二条从 $(1, 1) -> (i_2 - 1, j_2) -> (i_2, j_2)$ $f[k, i_1, i_2] = max(f[k, i_1, i_2], f[k - 1, i_1-1, i_2-1] + tmp)$ 第二种情况: 第一条从 $(1, 1) -> (i_1 - 1, j_1) -> (i_1, j_1)$, 第二条从 $(1, 1) -> (i_2, j_2 - 1) -> (i_2, j_2)$ $f[k, i_1, i_2] = max(f[k, i_1, i_2], f[k - 1, i_1-1, i_2] + tmp)$ 第三种情况: 第一条从 $(1, 1) -> (i_1, j_1 - 1) -> (i_1, j_1)$, 第二条从 $(1, 1) -> (i_2 - 1, j_2) -> (i_2, j_2)$ $f[k, i_1, i_2] = max(f[k, i_1, i_2], f[k - 1, i_1, i_2-1] + tmp)$ 第四种情况: 第一条从 $(1, 1) -> (i_1, j_1 - 1) -> (i_1, j_1)$, 第二条从 $(1, 1) -> (i_2, j_2 - 1) -> (i_2, j_2)$ $f[k, i_1, i_2] = max(f[k, i_1, i_2], f[k - 1, i_1, i_2] + tmp)$
如果两个格子重合
t
m
p
=
w
[
i
1
,
j
1
]
tmp = w[i_1,j_1]
tmp=w[i1,j1]
不重合则
t
m
p
=
w
[
i
1
,
j
1
]
+
w
[
i
2
,
j
2
]
tmp = w[i_1, j_1] + w[i_2, j_2]
tmp=w[i1,j1]+w[i2,j2]
i 1 = = i 2 i_1==i_2 i1==i2 代表两个格子重合
#include<bits/stdc++.h>
using namespace std;
const int N = 15;
int f[N * 2][N][N];
int w[N][N];
int n;
int main()
{
cin >> n;
int a, b, c;
while(cin >> a >> b >> c, a || b || c)
w[a][b] = c;
for(int k = 2; k <= n + n; k ++)
for(int i1 = 1; i1 <= n; i1 ++)
for(int i2 = 1; i2 <= n; i2 ++)
{
int j1 = k - i1;
int j2 = k - i2;
if(j1 >= 1 && j1 <= n && j2 >= 1 && j2 <= n)
{
int tmp = w[i1][j1];
if(i1 != i2)
tmp += w[i2][j2];
int &ff = f[k][i1][i2];
ff = max(ff, f[k - 1][i1 - 1][i2 - 1] + tmp);
ff = max(ff, f[k - 1][i1 - 1][i2] + tmp);
ff = max(ff, f[k - 1][i1][i2 - 1] + tmp);
ff = max(ff, f[k - 1][i1][i2] + tmp);
}
}
cout << f[n + n][n][n];
return 0;
}

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








