数据统计分析旨在通过统计学的数据分析方法，例如数据的统计特征，数据变量的分布等等统计方法来进数据在统计学的描述分析，再可以通过大数据可视化的手段将其可视化展示。
1.数据随机变量及其分布
1.1均匀分布及其随机数图
均匀分布在概率论中是一个十分重要且基础的分布，这里对均匀的定义是：
利用Python描述均匀分布为：
import numpy as np #加载numpy包
np.set_printoptions(precision=4) #设置numpy输出为4位有效数
a=0
b=1
n=20 # n表示在[a,b]中生成n个点
x=np.linspace(a,b,n); # [a,b]中n个等差数据
# x = np.linspace(0, 1, 20)
x
均匀随机数是基于均匀分布产生的随机数，具体如下：
利用Python代码生成一个均匀随机实数：
np.random.rand(1) #生成[0,1]上的一个随机实数:random.uniform(0,1) ,每次运行的结果，是不一样的 
利用Python代码生成一组均匀随机实数并可视化：
np.random.seed(123) #设置种子数seed可重复结果,可任意设置
R=np.random.rand(10)
R[:10] #[0,1]上的1000个随机数=np.random.uniform(0,1,1000)
plt.plot(R,'.');
还可以生成整数随机数、实数随机数等等：
# 整数随机数
import random
random.randint(10,20)
# 整数随机数列
import numpy as np
np.random.randint(10, 21, 9)
# 实数随机数列
np.random.uniform(0,1,10)
1.2正态分布及其随机数图
正态分布是统计推断中用到的最重要的分布之一，几乎涵盖了大部分大样本数据的分布。
利用Python代码生成标准正态分布曲线及其概率密度函数并可视化：
from numpy import arange,exp #arange类似linspace函数
from math import sqrt,pi
x=arange(-4, 4, 0.1) #x为-4到4上间距为0.1的数
x
y=1/sqrt(2*pi)*exp(-x**2/2)
y
plt.plot(x,y)
标准正态分布的取值(pdf)及分位数(ppf)介绍，及其计算代码如下：
import scipy.stats as st #加载统计方法包
p_z=st.norm.pdf(-2)
p_z #p(z)=1/sqrt(2*pi)*exp(-z**2/2);
za=st.norm.ppf(0.95)
za #单侧
[st.norm.ppf(0.025),st.norm.ppf(0.975)] #双侧
标准正态分布的概率计算方式如下：
p=st.norm.cdf(1.645)
p #标准正态分布下的面积：p=P(z≤1.645)的累积概率
在标准正态曲线上计算[a,b]上的概率并可视化其面积图的代码如下：
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as st
def norm_p(a, b):
# 定义x的范围
x = np.arange(-4, 4, 0.1)
y = st.norm.pdf(x)
# 计算区间[a, b]内的x和y值
mask = (a <= x) & (x <= b)
x1 = x[mask]
y1 = y[mask]
# 计算累积概率p
p = st.norm.cdf(b) - st.norm.cdf(a)
print("N(0,1)分布: [{:.2f},{:.2f}] p={:.4f}".format(a, b, p))
# 绘制图形
plt.figure(figsize=(10, 6))
plt.plot(x, y, label='Standard Normal Distribution PDF')
plt.fill_between(x1, y1, color='skyblue', alpha=0.5, label=f'Area between {a} and {b}')
plt.hlines(0, -4, 4, colors='black', linestyles='dashed')
plt.vlines([a, b], 0, [st.norm.pdf(a), st.norm.pdf(b)], colors='red', linestyle='--')
# 添加标题和标签
plt.title('Standard Normal Distribution Probability Density Function')
plt.xlabel('x')
plt.ylabel('Probability Density')
plt.legend()
# 显示图形
plt.grid(True)
plt.show()
# 示例调用
norm_p(-1, 1)
通过np.random.normal函数可以实现生成正态分布随机数图
#随机产生1000个标准正态分布随机数，作其概率直方图，然后再添加正态分布的密度函数线。
#np.random.seed(123) #设置种子数seed可使结果可重复
z1=np.random.normal(0,1,1000) #1000个标准正态分布随机数N(0,1)
z1[:20]
plt.hist(z1); 
检验数据的正态性是十分重要的统计分析手段，通过st.probplot函数可以绘制正态分布概率的检验图。
import scipy.stats as st #加载科学计算包scipy的统计功能
st.probplot(X,plot=plt)
2.统计量及抽样分布图
统计量及抽样的概念如下：
随机数抽样实例：
import pandas as pd
BSdata=pd.read_excel('./data/DaPy_data.xlsx','BSdata'); #读取学生数据
BSdata
i=np.random.randint(0,52,6);i #抽取6名学生，取[1,52]上的6个整数
BSdata.iloc[i] #获取抽到的6名学生信息 
2.1统计量的分布
2.1.1中心极限定理及其模拟图
正态均值的分布：
# 基于正态分布的中心极限定理模拟函数
import seaborn as sns
def norm_sim1(N=1000,n=10): # n为样本个数，N为模拟次数（即抽样次数）
xbar=np.zeros(N) # 产生放置样本均值的向量
for i in range(N): # 计算[0,1]上的标准正态随机数及均值
xbar[i]=np.random.normal(0,1,n).mean()
sns.distplot(xbar,bins=50) #plt.hist(xbar,bins=50)
print(pd.DataFrame(xbar).describe().T) #模拟结果的基本统计量
np.random.seed(1) #设置种子数seed使结果可重复
norm_sim1(10000,30) #根据默认值模拟
非正态均值统计量的分布 —— 渐近正态分布：
# 基于非正态分布的中心极限定理模拟函数
def norm_sim2(N=1000,n=10):
xbar=np.zeros(N)
for i in range(N): #计算[0,1]上的均匀随机数及均值
xbar[i]=np.random.uniform(0,1,n).mean()
sns.distplot(xbar,bins=50)
print(pd.DataFrame(xbar).describe().T)
np.random.seed(3) #设置种子数seed使结果可重复
norm_sim2() 
2.1.2均值的 t 分布及其图示
小样本正态均值的标准化统计量分布 — t分布：
t 分布曲线比较图：
x = np.arange(-4,4,0.1)
yn = st.norm.pdf(x,0,1)
yt3 = st.t.pdf(x, 3)
yt10 = st.t.pdf(x, 10)
plt.plot(x, yn, 'r-', x,yt3,'b.',x,yt10,'g-.')
plt.legend(["N(0, 1)", "t(3)", "t(10)"])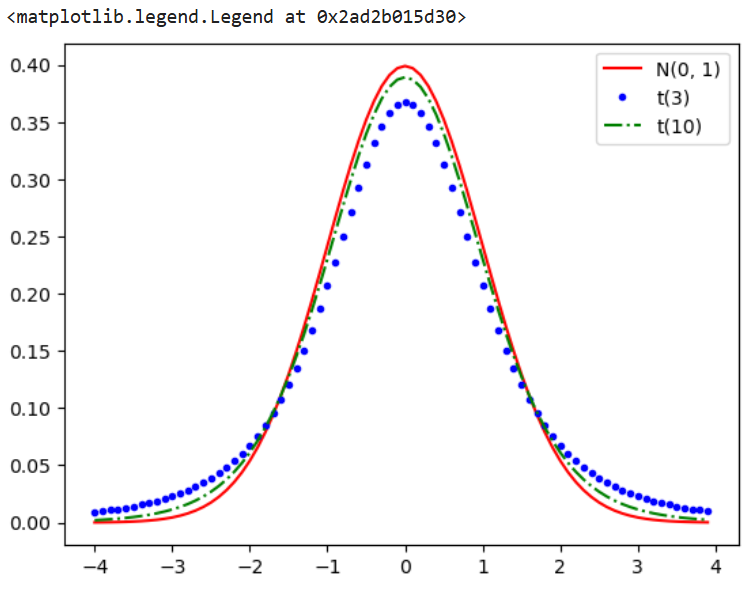
3. 基本统计推断方法
3.1参数的估计方法
3.1.1点估计
import pandas as pd
BSdata=pd.read_excel('./data/DaPy_data.xlsx','BSdata'); #读取学生数据
#BSdata
#均值的点估计
BSdata['身高'].mean()
#标准差的点估计
BSdata['身高'].std()
#比例的点估计
f=BSdata['开设'].value_counts();
p=f/sum(f)
p
3.1.2区间估计
norm_p(-2,2) 
# 定义t分布曲线下[a, b]上计算概率的面积图
import scipy.stats as st
def t_p(a,b,df=10): #t分布曲线下[a,b]上计算概率的面积图
x=np.arange(-4,4,0.1)
y=st.t.pdf(x,df)
x1=x[(a<=x) & (x<=b)];x1
y1=y[(a<=x) & (x<=b)];y1
p=st.t.cdf(b,df)-st.t.cdf(a,df);
print(" t("+str(df)+"): [%3.2f, %3.2f] p=%5.4f"%(a,b,p))
plt.plot(x,y);#plt.text(-0.7,0.2,"p=%5.4f"%p,fontsize=15);
plt.hlines(0,-4,4); plt.vlines(x1,0,y1,colors='r'); t_p(-2,2) #t:[-2,2], df=10
#基于原始数据的t分布均值和置信区间
def t_interval(x,b=0.95): #这里b为置信水平，通常取95%
a=1-b
n = len(x)
ta=st.t.ppf(1-a/2,n-1);ta
from math import sqrt
se=x.std()/sqrt(n)
return(x.mean()-ta*se, x.mean()+se*ta)
t_interval(BSdata['身高']) #身高均值的 95%的置信区间
3.2参数的假设检验
3.2.1样本均值 t 检验
#单样本 t 检验函数进行均值的 t 检验
print("样本均值：",BSdata.身高.mean())
st.ttest_1samp(BSdata.身高,popmean = 166)
3.3统计推断的可视化
3.3.1均值推断的可视化函数
#定义单样本均值t检验图
def ttest_1plot(X,mu=0,k=0.1):
df=len(X)-1 #df=n-1
t1p=st.ttest_1samp(X, popmean = mu);
x=np.arange(-4,4,k); y=st.t.pdf(x,df)
t=abs(t1p[0]);p=t1p[1]
x1=x[x<=-t]; y1=y[x<=-t];
x2=x[x>=t]; y2=y[x>=t];
print(" 样本均值： \t%8.4f "%X.mean())
print(" 单样本t检验: t=%6.3f p=%6.4f"%(t,p))
t_interval=st.t.interval(0.95,len(X)-1,X.mean(),X.std())
print(" t置信区间:\t(%7.4f, %7.4f)"%(t_interval[0],t_interval[1]))
plt.plot(x,y); plt.hlines(0,-4,4);
plt.vlines(x1,0,y1,colors='r'); plt.vlines(x2,0,y2,colors='r');
plt.vlines(st.t.ppf(0.05/2,df),0,0.2,colors='b');
plt.vlines(-st.t.ppf(0.05/2,df),0,0.2,colors='b');
plt.text(-0.6,0.2,r"$\alpha$=%3.2f"%0.05,fontsize=15);
ttest_1plot(BSdata.身高,166) #总体均值为166时的推断图 
学习心得：
通过借助Python中Numpy、Pandas库以及Matplotlib等强大的绘图库，可以很好的实现关于数据的统计分析与可视化，利用统计学的思想可以更好地获取数据的数据特征以揭示数据内在的规律。
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
