实现二叉树的前序,中序,后序遍历
—————————————————————————————
相信大家对二叉树已经很了解了,我以前写过一个二叉树的基本操作的博客,里面有很多二叉树的很多功能,比如高度,叶子结点
个
数什么的都很简单,
但是大多数都是递归实现的,可能思考过程会相比较简单一点,我当时没有写到二叉树的前序,中序,后序
前序遍历
我们知道前序遍历的顺序是 中 左 右,首先一棵树放到你的面前,你刚开始只能访问左边的节点,但是当你访问到它的下一个左节
点,
但是它的右节点待会还要访问呢,所以需要保存该节点,方便一会找到它的右节点,这里我们很容易想到栈,因为我们都知道
前序遍历的时候,一直访问到最左节点,接下来就会访问到,最左的右子树懂我的意思吗? 就拿这棵树来说,我们访问完3,肯定
要退回去,访问2的右子树,所以这里使用栈,后进先出,我们很自然的可以取到2这个节点.
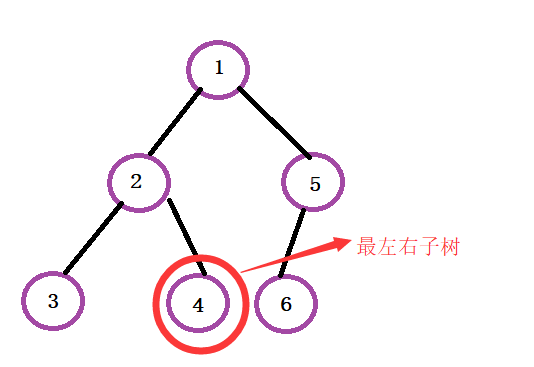
现在我们确定使用栈,接下来想接下来的运作思想,要怎么使用栈按照前序遍历的顺序访问完整颗树?首先肯定是一直把最左边这条
路径上的节点依次压进栈里面,我们现在需要注意观察我们
如何才能取得右边的节点呢?这里通过观察我们发现第一个访问到的右
子树节点4,是倒数第二个进入栈里面的节点的右节点,这时候呢我们要想办法取到2的怎么办,肯定是Pop掉3号节点,让我们可以
取得2号节点,然后访问到4,然后访问完4,再pop掉4号节点和2号节点,栈顶现在就是1号节点了,他就可以访问到右子树了,这是
一个最底层的子问题,其实整个树都可以使用子问题
这样解决,我们拿到每一个节点都执行这样的方法
,也就是无数个子问题的积
累,无论树有多复杂,它分接下来也会是这样样子,最后解决掉问题.思想现在是有的,让我们编写代码:
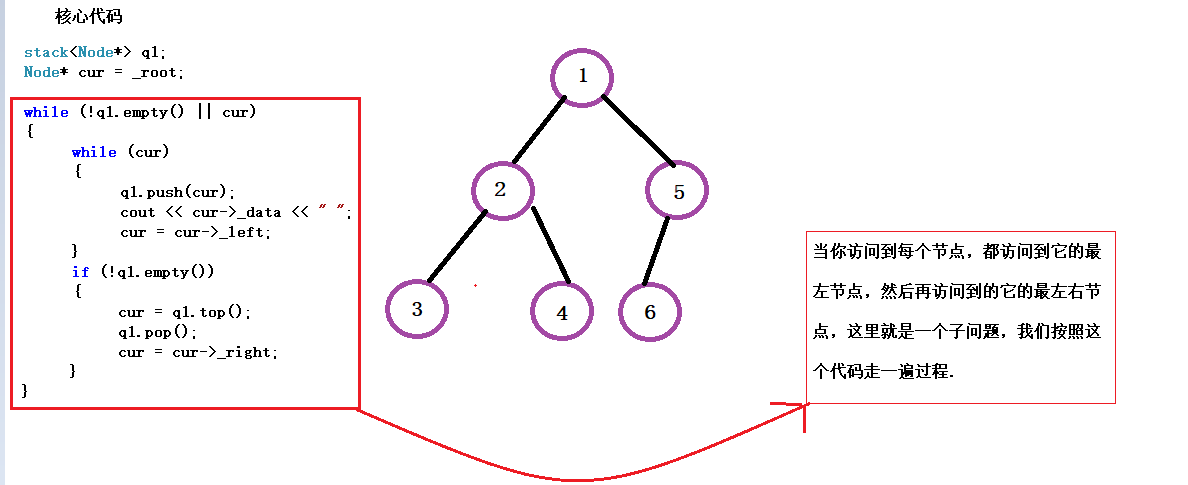
代码实现:
void PreOrder() //前序遍历
{
if (_root == NULL)
return;
stack<Node*> q1;
Node* cur = _root;
while (!q1.empty() || cur)
{
while (cur)
{
q1.push(cur);
cout << cur->_data << " ";
cur = cur->_left;
}
if (!q1.empty())
{
cur = q1.top();
q1.pop();
cur = cur->_right;
}
}
}
中序遍历
其实中序遍历的过程和前序基本一样,只不过讲输出语句换了一个地方而已,具体过程还是一样的,我直接附上代码,相信你会写
前序遍历,就一定会写中序遍历.
void InoOrder()//中序遍历
{
if (_root == NULL)
return;
Node* cur = _root;
stack<Node*> q1;
while (!q1.empty() || cur)
{
while (cur)
{
q1.push();
cur = cur->_left;
}
if (!q1.empty())
{
cur = q1.top();
cout << cur->_data << " ";
q1.pop();
cur = cur->_right;
}
}
}
后序遍历
我们终于走到了最难的后序遍历了,大家是不是觉得这就跟前面也没啥区别啊,也就是换一下输出语句的位置? 这里其实并不是这
样的,下面这个例子就是这里可能会出现的问题.
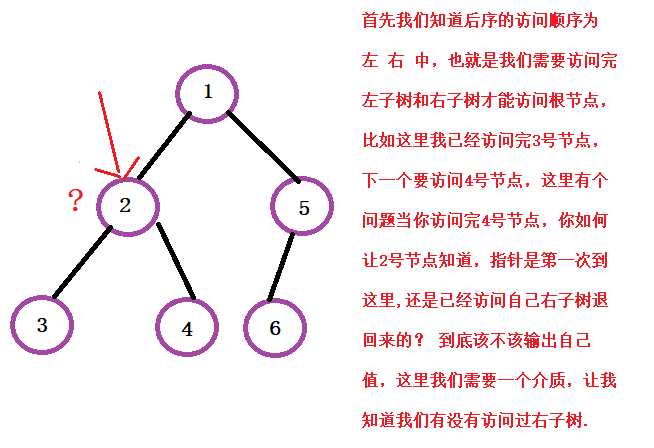
这里我们很容易使用一个前驱指针prev,记录我们的指针上一个的访问对象,如果我发现prev是我的右子树的根,那么我就可以输
出我的值,然后pop掉,所以一个节点Pop掉的条件就是 :没有右节点为空还有右节点已经访问过.剩下的就是正常的压栈进栈。
代码实现:
//非递归后序遍历
void PosOrder()
{
assert(_root != NULL);
Node* cur = _root;
Node* prev = NULL;
stack<Node*> q;
while (!q.empty() || cur)
{
while (cur)
{
q.push(cur);
cur = cur->_left;
}
Node* top = q.top();
if (top->_right == NULL || top->_right == prev) //可以访问的情况
{
cout << top->val << " ";
q.pop();
}
else //说明它的右子树并没有访问完毕,该节点不能被访问并pop
{
cur = top->_right;
}
prev = top;
}
cout << endl;
}
这里就是最基本的三种非递归遍历方式,我们更多的是要思考为什么这么要这样做,而不是记住方法就好了,多想想方法是怎么想
出来的,锻炼自己的思维方式,这样才是实现这些算法的最重要的目的,并不是单纯的刷题.
























 1247
1247

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








