第五章 图的基本概念 5.3 图的矩阵表示

5.3 图的矩阵表示

本节讨论图的关联矩阵，邻接矩阵，可达矩阵。

无向图的关联矩阵

这里的关联是指点与边之间的关联。如图：

这个无向图的关联矩阵为：

• 矩阵的每一行代表一个点与各边之间的关系。所以第$i$行元素之和为$v_i$的度数。
• 每一列代表一条边与各点之间的关系。所以每一列恰好有两个1（一条边的两个端点）或者一个2（环）。
• 矩阵中各元素之和等于$2m$（边条数的2倍）。

有向图的关联矩阵

还是点与边之间的关联。当点是边的起点时，记为1。当点是边的终点时，记为-1。不关联记为0。

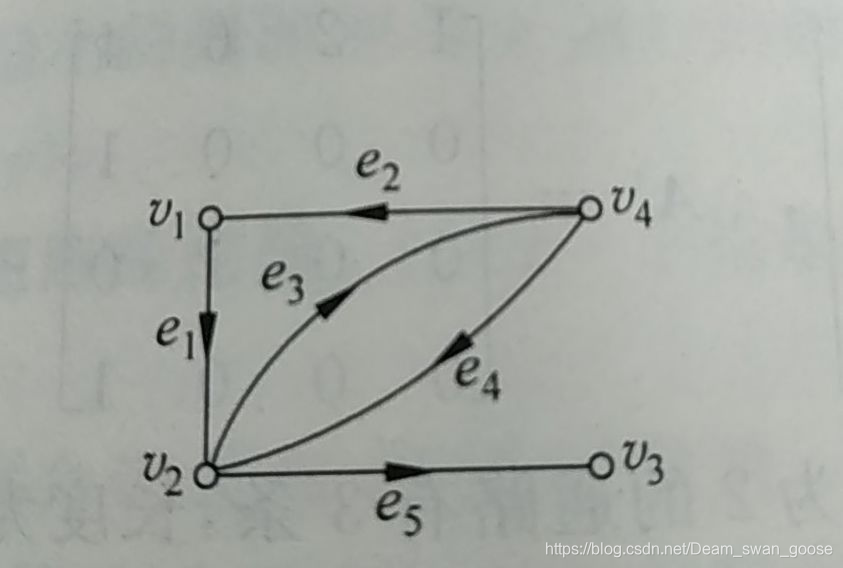
这个有向图的关联矩阵为：

• 每一行代表一个点，1的个数表示其出度，-1的个数代表其入度。
• 每一列代表一个边，所以恰好有一个1和-1。

有向图的邻接矩阵

其表示点与点之间的邻接（通过一条边就可相连）。如图：

• 第$i$行的元素和等于$v_i$的出度。
• 第$j$列的元素和等于$v_j$的入度。
• 因为这是有向图的邻接矩阵，每条边只沿其方向计算一次。所以矩阵里各元素和等于$m$（边数）

$A^1$表示长度为1的通路条数，$A^2$表示长度为2的通路条数……以此类推。
eg：
$A^3$中第一行第二列的2就表示：$v_1$到$v_2$有长度为3的两条通路。

有向图的可达矩阵

这里的可达是指两点之间的可达。沿有向图只要可达就记做1，不可达记做0。如图：

这个有向图的可达矩阵为：

• 因为任何顶点到自身都是可达的，所以可达矩阵主对角线上的元素恒为1。

练习1：



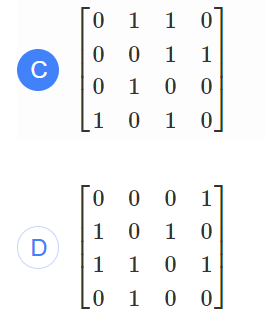
练习2：

练习3：


练习4：

(1) D是哪类连通图?

答：D中存在经过所有顶点的通路,但无经过所有顶点的回路,因而它是单向连通的,但不是强连通的.

(2) D中长度为1、2、3、4的通路各有多少条? 其中有多少条回路?