第一章 概率论的基本概念 1.5 条件概率

1.5 条件概率

条件概率

用图形来理解P（A|B）求的就是A和B的交集所占B的比例。

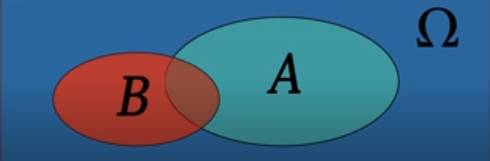
条件概率的性质：

例：

解：

解析：

• 从左往右是我们先心里想好在这种条件下是什么情况，再去求解。遇到简单的一般用这种方法。
• 从右往左是用定义里的公式去做。

练1：



练2：

练3：

易错题：

解析：
这个不能想当然的写成$\frac{1}{3}$.因为条件是“其中有一件是不合格”而不是“第一件是不合格的”。这里只要至少有一件是不合格的ok了。正确解法如下：

乘法定理

两个事件的标准形式：

一般形式：

这个一般形式很少有，但是当$n=3$时用的比较多。如下:

$P(ABC)=P(A)\cdot P(B|A)\cdot P(C|AB)$

宋老师讲的理解办法挺好的：

• 先走一步A
• 在A的基础上再走一步B
• 在走过了AB的基础上再走最后一步C

例1：

例2：

辨析 $P(AB)$ 与 $P(A|B)$:

全概率公式

定义：

其实就是把每一个小部分的概率求加和就是要求的整体的概率。

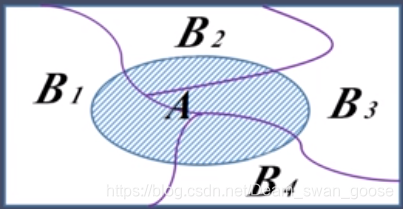
$A$在$B_1$上的概率是：$P(A{B}_1)$ = $P(A|B_1)$ ·$P(B_1)$

……

依次类推，A的4个小部分的加和就是A整体的概率。

例：

贝叶斯公式

• 贝叶斯公式的分母是全概率公式
• 贝叶斯公式的分子是全概率公式中的一个部分，也可以用乘法公式来改变形态。
• 贝叶斯公式算出来的概率是某个小部分占整体的比重。可以用来分析哪个小部分对整体的影响最大。
• 贝叶斯公式是全概率公式的逆过程。全概率公式是由部分去求整体，贝叶斯公式是由整体去逆推各部分的影响。

例：

假设某种新型冠状病毒的发病率是$0.0004$，现在有一种检测方法对患有此病的人检测成功率为99%,对于没有患病的人有0.1%的误诊率。求下列两件事情发生的概率：
<1> 若检测结果为阳性（患病），但是却没有感染的概率是多少？

<2>若检测结果为阴性（未患病），但是却被感染的概率是多少？

到这里笔者就要感慨一番了，我们把两个共识作为条件：
<1>大多数事物都是正态分布的，即越靠近两个极端概率越小。（本题体现为0.0004）
<2>误差总是存在的，不可能达到完美的100%状态。（本题体现为99%和99.9%）

在计算的过程中我们发现这0.0004的极端黑暗抑制了99%的绝望，催生了0.1%的希望。原来走入0.0004的极端黑暗会看见71.6%的光明。这看似对立的两个极端以一种奇妙的方式相互关联着，这便是我们常说的物极必反，否极泰来，乐极生悲，看似彼此相离却又终生相依……

果然，科学的尽头是玄学。

练1：

这道题题干也可以换成抽红包抽最佳，无论第几个抽每个人抽到最佳的概率都是$\frac{1}{n}$。由此可见，抽签是很公平的。

练2：