数电笔记——第二章 逻辑代数基础（二）

2.5 逻辑函数及其描述方法

一、逻辑函数

逻辑关系中输出变量与输入变量之间是一种函数关系-------逻辑函数

Y=F(A，B，C，……)

输入、输出变量的取值只有“0”和“1” ------二值逻辑函数

任何一件具体的因果关系都可以用一个逻辑函数来描述。

二、逻辑函数的描述方法

1、逻辑真值表

真值表：将输入、输出的所有可能状态一一对应地找出来，列成表格。

真值表是唯一的

[注意]n个变量可以有2ⁿ个组合，一般按n位二进制数的顺序，输出与输入状态一一对应，列出所有可能的状态。

2、逻辑函数式

 

3、逻辑图

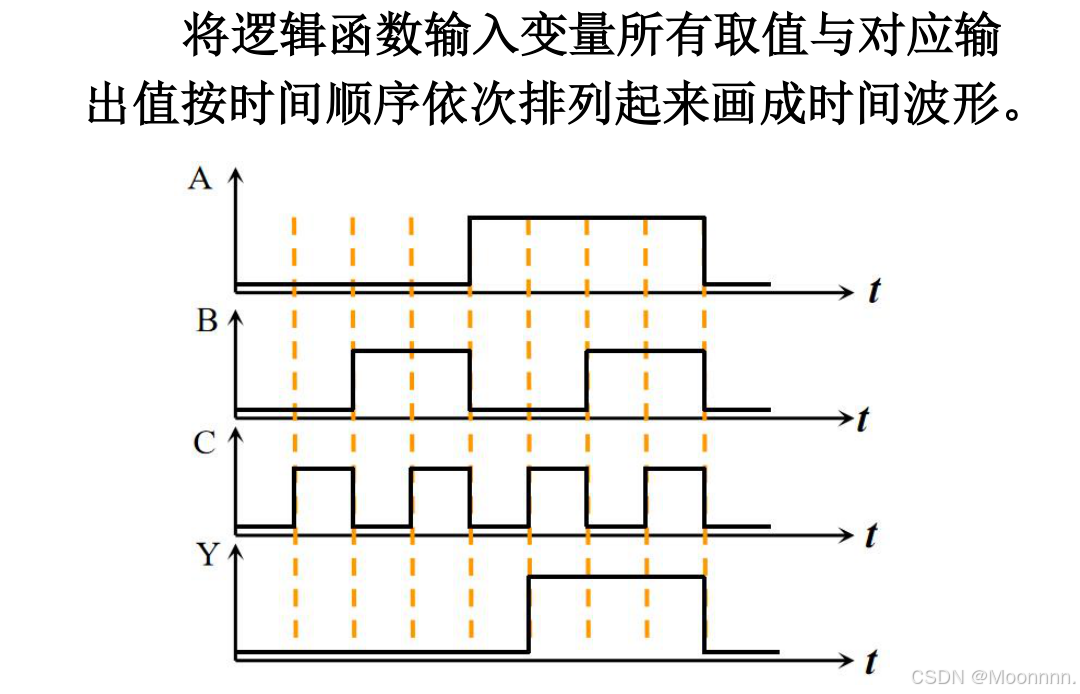
4、波形图

 逻辑函数的表示方法

（1）逻辑真值表：将输入变量所有的取值下对应的输出值找出来，列成表格。

（2）逻辑函数式：把输出与输入之间的逻辑关系写成与，或，非等运算的组合式。

（3）逻辑图：将逻辑函数中各变量之间的与、或、非等逻辑关系用图形符号表示出来。

（4）波形图：将输入变量所有取值可能与对应输出按时间顺序排列起来画成时间波形。

5、各种表示方法之间的相互转换 

1>真值表 <--> 逻辑函数式

（1）真值表——逻辑函数式

一般分为下面三步：

首先，找出真值表中使逻辑函数Y=1的输入变量取值组合；

其次，每组输入变量取值的组合对应一个乘积项，其中取值为1的写原变量，取值为0的写反变量；

最后，将这些乘积项相加，即得到Y的逻辑函数式。

（2）逻辑式——真值表

将输入变量取值的所有组合状态逐一 代入逻辑式求出函数值，列成表。

2>逻辑式 <--> 逻辑图

（1）逻辑式——逻辑图

用图形符号代替逻辑式中的运算符号 并按运算的优先顺序将符号连接起来。

（2）逻辑图——逻辑式

从输入端到输出端逐级写出每个图形符号对应的逻辑式。

3>波形图转换为逻辑式

一般分为下面三步：

首先，找出波形图中使输出变量等于1的每个时间段输入变量取值组合；

其次，每组输入变量取值的组合对应一个乘积项，其中高电平写原变量，低电平的写反变量；

最后，将这些乘积项相加，即得到Y的逻辑函数式。

三、逻辑函数的两种标准形式

1、最小项

最小项 m ：

① m 是乘积项

②包含 n 个因子

③ n 个变量均以原变量 / 反变量的形式

在 m 中出现一次

 最小项的重要性质：

1. 在输入变量的任何取值下必有一个最小项，而且仅有一个最小项的值为1。
2. 全体最小项之和为1。
3. 任意两个最小项的乘积为0。
4. 具有相邻性的两个最小项之和可以合并成一项并消去一对因子。

[补] 若两个最小项只有一个因子不同，则称这两个最小项具有相邻性。

2、最大项 

最大项 M：

① M 是相加项；

②包含 n 个因子

③ n 个变量均以原变量 / 反变量的形式

在 M 中出现一次

 

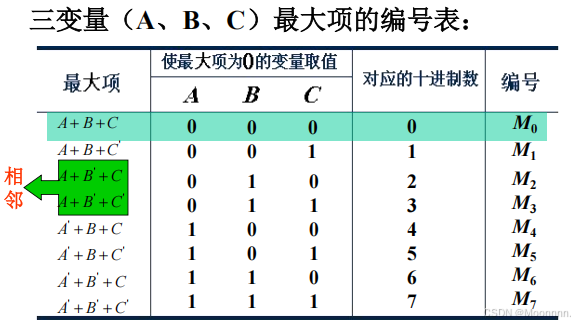
 最大项的重要性质：

1. 在输入变量的任何取值下必有一个最大项，而且仅有一个最大项的值为0。
2. 全体最大项之积为0。
3. 任意两个最大项之和为1。
4. 只有一个变量不同的两个最大项的乘积等于各相同变量之和。

 

3、逻辑函数的两种标准形式

1>逻辑函数的最小项之和形式——标准与或式

如果在一个与或表达式中，所有与项均为最小项，则称这种表达式为最小项表达式，或称为标准与或式、标准积之和式。

利用基本公式 A + A' = 1 可以把任何一个逻辑函数化为最小项之和的标准形式。

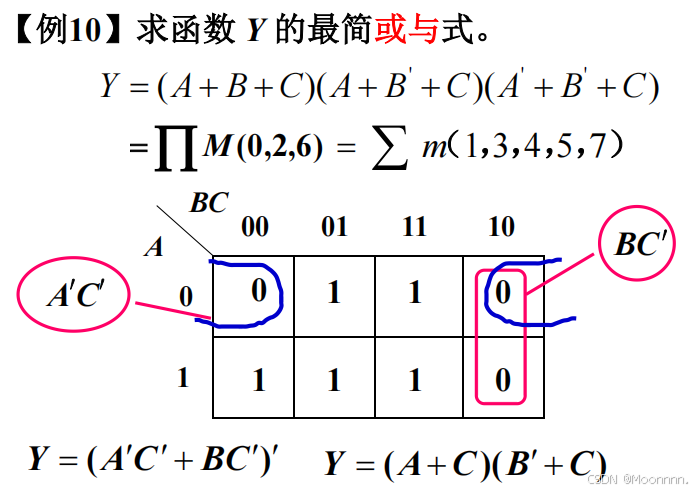
 2>逻辑函数的最大项之积形式——标准或与式

利用基本公式 A · A' = 0 可以把任何一个逻辑函数化为最大项之积的标准形式。

如果已知逻辑函数 Y=∑mᵢ 时，定能将Y化成编号 i 以外的那些最大项的乘积。

2.6 逻辑函数的化简方法

逻辑函数的最简形式

最简与或式 ------包含的乘积项最少，每个乘积项的因子也最少，称为最简的与或逻辑式。

一、公式化简法

公式法化简的原理是反复使用逻辑代数的基本公式和常用公式消去函数式中多余的乘积项和多余因子，来得到最简函数形式。

1、并项法

利用公式 AB + AB' = A 将两项合并成一 项，并消去互补因子。

2、吸收法 

利用公式 A + AB = A   消去多余的乘积项。

3、消项法

利用公式 AB + A'C + BC = AB + A'C 消 去多余的乘积项。

4、消因子法

利用公式 A + A'B = A + B 消去多余的因子。

5、配项法

利用公式 A + A = A 和 A + A' = 1 先配项或 添加多余项，然后再逐步化简。

公式 法 化简

优点是：不受变量数目的限制。

缺点是：没有固定的步骤可循；需要熟练运用 各种公式和定理；在化简一些较为复杂的逻 辑函数时还需要一定的技巧和经验；有时很 难判定化简结果是否最简。

逻辑函数的花间结果不一定唯一。 

二、卡诺图化简法

1、逻辑函数的卡诺图表示法

1>表示最小项的卡诺图

将n变量的全部最小项（2ⁿ）用小方块表示，并且使逻辑相邻的最小项几何位置也相邻，所得到的方格图即为n变量最小项的卡诺图。

 2>用卡诺图表示逻辑函数

用卡诺图表示逻辑函数，首先将函数式化成最小项和的形式；在函数式中包含的最小项在卡诺图相应的位置填1，其余位置填0。

2、用卡诺图化简逻辑函数

1>合并最小项的规则

依据：具有相邻性的最小项可以合并，消去不同的因子。

在卡诺图中，凡是几何位置相邻的最小项均可以合并。

 两个最小项相邻且组成矩形框，可以合并成一项，消去一个不同的因子。

四个最小项相邻且组成矩形框，可以 合并成一项，消去两个不同的因子。

 

思考： 八个最小项相邻且组成矩形 框，情况怎样？

八个最小项相邻且组成矩形框，可以 合并成一项，消去三个不同的因子。

2>卡诺图化简的步骤

（1）将函数化成最小项之和的形式

（2）填卡诺图

（3）合并最小项

（4）将各乘积项相加，即得到最简与或式

合并最小项的规则

化简后的乘积项应包含函数式的所有最小项，即覆盖图中所有的“1” 。

乘积项的数目最少，即圈成的矩形框数目最少。

每个乘积项因子最少，即圈成的矩形框最大。

[总结] 

（ 1 ）圈成的矩形框越大越好；

（ 2 ）各最小项可以重复使用，但是每个 矩形框至少包含一个新项；

（3 ）必须圈完所有为 “1” 的最小项；

（ 4 ）注意“相接” 、 “相对”都相邻；

（ 5 ）圈圈时先圈大圈，后圈小圈；

（ 6 ）尽可能圈大圈，少圈圈；

（ 7 ）圈法不唯一，结果可能也不唯一。

 

卡诺图化简法

优点：简单、直观、有一定步骤可循，易掌握，易避免差错。

缺点：变量超过5个以上时，实用意义不大。。

2.7 具有无关项的逻辑函数及其化简

一、几个概念

约束：对输入变量取值所加的限制。

约束项：某种制约关系的最小项，恒等于0。将约束项写入逻辑式中不影响函数值。

约束条件：所有约束项的组合构成的逻辑式。

任意项：对于某些输入变量取值下函数值为1、0皆可，不影响电路的功能，把这些输入变量使输出为1的最小项。

无关项：约束项和任意项的统称。

二、具有无关项的逻辑函数化简

采用卡诺图化简函数时，可以利用无关项(×)来扩大矩形框：如果加无关项(×)后矩形框增大，则视无关项(×)为1；否则视无关项(×)为0。

利用无关项可以使得函数进一步简化。

2.9 逻辑函数形式的变换

一个逻辑函数的真值表是唯一的，而函数表达式却有很多，常用的有与或、与非 - 与非、或非－或非、与或非等，它们之间可相互转换。

注：本文出自对 河北科技大学数字电路技术基础课程任老师 上课内容的学习笔记。