16. 【C语言】从(0,0)到(m,n)，每走一步只能向上走或者向右走，则有多少种走法（Demo）

问题描述：
在如下图中，从(0,0)到(m,n)，每走一步只能向上走或者向右走，则有多少种走法？

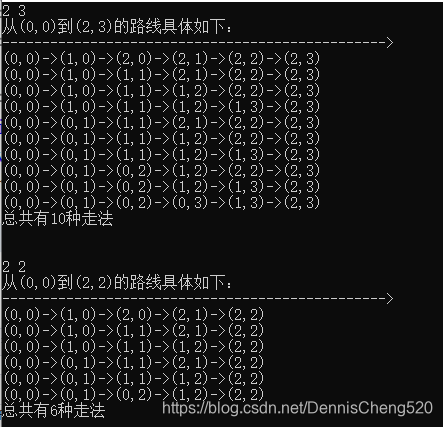
例如，从(0,0)到(2.3)有如下10条路径：
(0,0)->(1,0)->(2,0)->(2,1)->(2,2)->(2,3)
(0,0)->(1,0)->(1,1)->(2,1)->(2,2)->(2,3)
(0,0)->(1,0)->(1,1)->(1,2)->(2,2)->(2,3)
(0,0)->(1,0)->(1,1)->(1,2)->(1,3)->(2,3)
(0,0)->(0,1)->(1,1)->(2,1)->(2,2)->(2,3)
(0,0)->(0,1)->(1,1)->(1,2)->(2,2)->(2,3)
(0,0)->(0,1)->(1,1)->(1,2)->(1,3)->(2,3)
(0,0)->(0,1)->(0,2)->(1,2)->(2,2)->(2,3)
(0,0)->(0,1)->(0,2)->(1,2)->(1,3)->(2,3)
(0,0)->(0,1)->(0,2)->(0,3)->(1,3)->(2,3)

问题分析：

1. 需要了解一个思路，由于只能向上走或者向右走，所以不管选择什么路线走，向上走的总长度为n，向右走的总长度为m，到达(m,n)的路线长度为m+n，打印显示的每条路径上有（m+n+1）个坐标。
2. 该问题可以理解为深度优先搜索的问题，利用递归，不断向下搜索，直到到达坐标(m,n)。其深度优先搜索树为：
   
3. 因为是坐标变化，涉及到两个变量的变化，则可以用二维数组。但是不能误解二维数组path[x][y]当成坐标表示。其实只需要path[2][N]就可以,这是一个两行N列的二维数组。第一行存放横坐标，第二行存放纵坐标，则每一个坐标可以表示成（path[0][i]，path[1][i]）

算法思想：

1. 定义一个二维数组path[2][N]，依次存放每条路径上的坐标。比如，上述深度优先生成树最左边的那条路径在二维数组path中的存放形式为：
   
2. 到达(m,n)上一步的路线只有两类：(m-1,n)->(m,n)或者(m,n-1)->(m,n)；同样从(0,0)出发也只有两种走法，要么向右走到(1,0)，要么向上走到(0,1)，所以对于每一个还没有到达(m,n)的坐标(x,y)，这些坐标下一步走法在坐标上的变化为：(x,y)->(x+1,y)或者(x,y)->(x,y+1)，由此可以发现递归的关系。
   
3. 在每一次搜索路径函数的过程中，首先需要将坐标的数值存入二维数组对应的位置上：

path[0][path_len] = x;		//将上一次递归传递的横坐标存放到二维数组对应的位置上
path[1][path_len] = y;		//将上一次递归传递的纵坐标存放到二维数组对应的位置上

其实横坐标和纵坐标在二维数组中所在的列数大小刚好是当前搜索到的路径长度path_len，该条路线下一个坐标在二维数组中的位置刚好对应path[0][path_len+1]、path[1][path_len+1]。

案例效果：

完整代码如下：

#include<stdio.h>
#include<stdlib.h>

#define N 20
int m, n;
void searchpath(int x, int y, int path_len, int *pcount, int path[][N])
{
	path[0][path_len] = x;		//将上一次递归传递的横坐标存放到二维数组对应的位置上
	path[1][path_len] = y;		//将上一次递归传递的纵坐标存放到二维数组对应的位置上
	if (x > m || y > n)
		return;		//只要x、y越界，直接本次递归
	else if (m == x && n == y)		//当x=m且y=n时表示已经到达(m,n)，即该条路径搜索完毕
	{
		(*pcount)++;	//用于计数，搜索到一条路径就+1
		for (int i = 0; i <= path_len; i++)			//按照路线格式打印当前的二维数组
		{
			if (i == path_len)
				printf("(%d,%d)\n", path[0][i], path[1][i]);
			else
				printf("(%d,%d)->", path[0][i], path[1][i]);
		}
		return;		//该条路径打印完毕，本次递归结束
	}
	searchpath(x + 1, y, path_len + 1, pcount, path);		//向右走，横坐标+1，纵坐标不变，当前路径长度+1
	searchpath(x, y + 1, path_len + 1, pcount, path);		//向上走，横坐标不变，纵坐标+1，当前路径长度+1
}

int main()
{
	int path[2][N];		//二维数组用于搜索某条路径时，依次记录该条路径的每个坐标
	int count = 0;
	while (scanf("%d%d", &m, &n) != EOF)
	{
		
		printf("从(0,0)到(%d,%d)的路线具体如下：\n", m, n);
		printf("------------------------------------------------>\n");
		searchpath(0, 0, 0, &count, path);
		printf("总共有%d种走法\n", count);
		count = 0;		//count清0，便于多次输入验证
		printf("\n\n");
	}
	system("pause");
}