组合数学引论部分习题答案

第一章

第6题 证明：从1，2，…，200个数中取100个整数，其中之一小于16，那么必有两个数，一个能被另一个整除

假设命题成立.
首先将1-200按照连续除以2,直到不能被2整除的结果分为100组,即:
1,1*2,1*4,...
3,3*2,3*4,...
...
197
199
每一组中的数都能互相整除.所以如果想取100个不能互相整除的数,只能每个组取一个.设取的数为
a1 = 1*2^k1
a3 = 3*2^k3
a5 = 5*2^k5
...
a199 = 199*2^k199
设那个小于16的数为ai=i*2^ki,i>=1.
则a3i=3i*2^k3i,于是k3i<ki,即k3i<=ki-1否则ai将整除a3i
ai<16

a3i=3(i*2^k3i)<=3(i*2^ki-1)=3*ai/2<3*16/2=24 以此类推
a9i=3*a3i/2<3*24/2=36

a27i=3*a9i/2<54
a81i=3*a27i/2<81
而a81i=81*（i*2^k81i)>=81 故矛盾,所以假设不成立.命题得证明.

第9题 在坐标平面上任意给定13个整点（两个坐标均为整数的点）则必有一个以他们中的三个为顶点的三角形其重心也是整点

三角形重心坐标为（(x1+x2+x3)/3,(y1+y2+y3)/3);这道题的关键就是适当地分类。

对13个点的x,y分别考虑，对于所有的x（共13个）来说，按照除以3以后的余数来划分，
可以分为0,1,2三类，其中必有一类为5个或以上(抽屉原理).
对于这一类的5个点，任意取三个的话，它们的重心的x坐标为整数。
考虑它们的y值，也可以分为余数为0,1,2三类,假如某一类有超过3个元素的话，取得
这三个点的y值，他们的重心的y坐标为整数。

如果没有任何一个类有超过3个元素的话，从这三个类中各取一个元素，即可得到
重心y坐标为整数的三角形。

第13题 计数从（0，0）点到（n，n）点的不穿过直线y=x的非降路径数。

先考虑对角线下方的路径，这种路径都是从（0，0）点出发经过（1，0）点及（n，n-1）点到达（n，n）的。

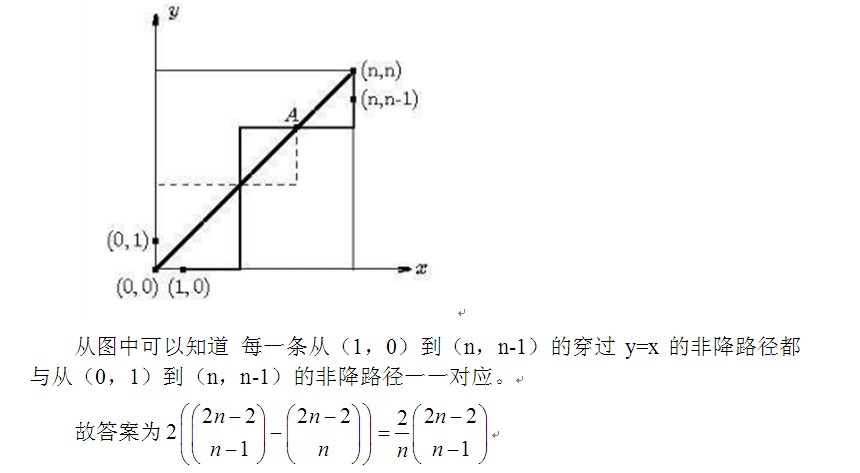
（本文大部分内容转自博客园NashZhou的博客，在此对上述公式空号中的两项相减进行解释，因为我本人也看了很久才看明白。第一项是从（1,0）到（n,n-1）的所有非降路径数，第二项是从（0,1）到（n,n-1）的所有非降路径数。由于从（0,1）到（n,n-1）是必会经过y=x的，而其与从（1,0）到（n,n-1）且要经过y=x是一一对应的，所以第二项也是从（1,0）到（n,n-1）的所有经过y=x的非降路径数。  想了很长时间的原因是，我把它给的“从（0,1）到（n,n-1）”看成了从“（0,1）到（n-1,n）”，然后得出下面式子中的2倍。。）

 

 第22题（1）5个0，4个1组成的字符串中，出现01或10的次数为4的不同字符串个数

（2）一般地，n个0，m个1组成的字符串中，出现01或10的次数为k的不同字符串个数