前言:这是学校多元统计分析课程布置的实验(包括基于python的线性代数运算、线性回归分析实验、聚类分析、因子分析和主成分分析),这里分享出来,注解标注的比较全,供大家参考。
1、文件“test4-1.csv”给出的是52名学生的数学(x1)、物理(x2)、化学(x3)、语文(x4)、历史(x5)和英语(x6)成绩。使用数据完成以下内容。
①使用SPSS的因子分析功能对数据进行因子分析;





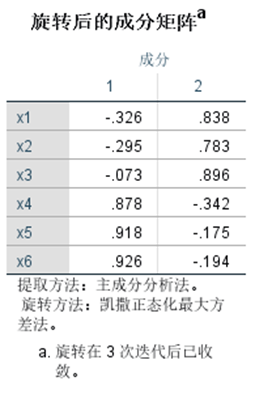

②使用python语言编程实现因子分析的功能,并运行上述数据,输出结果:因子载荷和因子得分,与SPSS因子分析结果进行比较。
import numpy as np
import pandas as pd
from sklearn.decomposition import PCA, FactorAnalysis
from sklearn import preprocessing
from factor_analyzer import FactorAnalyzer
# 取消科学计数法
np.set_printoptions(suppress=True)
df = pd.read_csv("test4-1.csv")
columns = df.shape[1]
data = df.columns[1: columns]
df = np.array(df[data])
# 皮尔森相关系数
df_corr = np.corrcoef(df)
# 数据标准化
df_z = preprocessing.scale(df)
# pca = PCA(n_components=2)
# 主成分得分
# newData = pca.fit_transform(df)
# print(newData)
# 累计方差
# print(pca.explained_variance_ratio_)
# print("公因子方差:\n", fa.get_communalities())
"""
因子得分就是以成分矩阵(载荷因子)作为系数构成一个线性组合(待确认)
这里不使用主成分分析的方法结果与SPSS一致
"""
# print("\n因子载荷矩阵:\n", fa.loadings_)
# variance = fa.get_factor_variance()
# print("\n特征值:\n", variance[0])
# print("\n方差贡献率:\n", variance[1])
# print("\n方差累计贡献率:\n", variance[2])
fa = FactorAnalyzer(rotation=None, n_factors=2, method='principal')
fa.fit(df_z)
print("载荷矩阵:\n", fa.loadings_)
# 使用最大方差法旋转因子载荷矩阵
# fa_is = FactorAnalysis(rotation='varimax', n_components=2)
fa_er = FactorAnalyzer(rotation='varimax', n_factors=2, method='principal')
fa_er.fit(df_z)
print("旋转后的载荷矩阵:\n", fa_er.loadings_)
print("\n因子得分(6项):\n", fa_er.transform(df_z)[:6])
运行结果

2、文件“test4-2.xlsx”的数据八项男子田径赛运动记录:100米(秒)、200米(秒)、400米(秒)、800米(秒)、1500米(分)、5000米(分)、10000米(分)、马拉松(分)。使用数据完成以下内容。
①使用SPSS的因子分析功能对数据进行主成分分析;






②使用python语言编程实现数据的Z值标准化和主成分分析的功能,运行上述数据,输出结果:主成分的方差贡献率、累计方差贡献率、载荷(因子负荷量)以及选择适合的主成分个数构建主成分表达式,与SPSS主成分分析结果进行比较。
import numpy as np
import pandas as pd
from factor_analyzer import FactorAnalyzer
from sklearn.decomposition import PCA, FactorAnalysis
from sklearn import preprocessing
import math
df = pd.read_csv("test4-2.csv")
columns = df.shape[1]
data = df.columns[2: columns]
df = np.array(df[data])
# 数据标准化
df = preprocessing.scale(df)
# 协方差矩阵的特征值和特征向量
pca = PCA(n_components=8)
# 主成分得分
pca.fit(df)
# 载荷(因子负荷量)
print("载荷(因子负荷量):\n", pca.components_[0])
pca.fit(df) # 训练PCA模型
print("pca模型得到的特征值(从大到小):", pca.explained_variance_, sep='\n')
# 因子载荷
# eigValues, eigVectors = np.linalg.eig(pca.components_)
# print(eigVectors)
# print(eigVectors * (eigValues ** 0.5))
pvr = pca.explained_variance_ratio_ # 返回各个成分各自的方差百分比
print("各个成分的方差百分比:", pvr, sep='\n')
ca = np.cumsum(pvr) # 计算累计贡献率
print("累计贡献率:", ca, sep='\n')
coefficient = []
j = 0
for i in pca.components_[0]:
coefficient.append(round(pca.components_[0][j], 4))
j = j + 1
# print("方差贡献即特征值的算术平方根:\n", sqrt)
# print("主成分系数:\n", coefficient)
x = []
for i in range(len(coefficient)):
x.append(round(coefficient[i], 8))
print(
"主成分表达式:Z = {}*X1+{}*X2+{}*X3+{}*X4+{}*X5+{}*X6+{}*X7+{}*X8".format(x[0], x[1], x[2], x[3], x[4], x[5], x[6], x[7]))
运行结果
主成分表达式中的系数大致等于SPSS中成分矩阵/根号下对应总方差解释

源码























 4万+
4万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








