文章目录
零、前言
0.连续与离散
具体 = 连续 + 离散
concrete = continuous + discrete

1.课程占比
1.第9周,当堂闭卷,占比50%
2.前8周,平时分50%:
(1)两次作业(1+2章、3+6+8章),各占10%,共20%
(2)一次交流,占20%:讲作业、成套法【第7-8周】
(3)研究报告,10%
要求:
上课、看书、做题目
2.期末考试复习
1.第二章:
第二章2.6必考。第一章和第二章是基础,主要是与其他章节题目相结合
2.第三章:
①轮盘赌 改为平方根
②P33 作业 证明(1)(2),什么条件下成立,什么条件下不成立

③Σ根号k向下取整,期末考试改成立方根k
3.第六章:
①调和数的题目,见复习资料。(与第二章2.6节有关)
②调和数的扩展,分母上是指数,黎曼函数,2.31
4.第八章:
①概率生成函数
②累积量的性质。例题,见复习资料。要弄懂细节。
③期望值、均值的两种计算方法
课件8-1 P12页下面两个Σ相等,怎么证明?

④课件8-1 P13 (3)证明 E(XY)=EX·EY
从第一行到第二行是相等的
3.2025年4月期末考试真题
5道大题:
一、黎曼函数
考试题目:求 ∑ k ≥ 1 ( ζ ( 2 k ) − 1 ) \sum\limits_{k≥1}(ζ(2k)-1) k≥1∑(ζ(2k)−1) 的封闭解或值
出处:课本第二章课后题 P54 2.31

二、数学期望
考试题目:证明:E(XY)=E(X)·E(Y)
出处:课件 8-1 P13
注意第一行到第二行之间有点跳跃,章老师说需要再补充过程

三、取下函数 (Floor Function)、取上函数 (Ceiling Function)
考试题目:
证明
(1)
⌈
⌈
x
⌉
3
⌉
=
⌈
x
3
⌉
⌈\sqrt[3]{⌈x⌉}⌉ = ⌈\sqrt[3]{x}⌉
⌈3⌈x⌉⌉=⌈3x⌉
(2)
⌈
x
3
⌉
=
⌈
x
⌉
3
⌈x^3⌉=⌈x⌉^3
⌈x3⌉=⌈x⌉3
出处:课件 3-1 作业

参考答案:

四、调和数
考试题目:求 S n = ∑ 1 ≤ k ≤ n H k k S_n=\sum\limits_{1≤k≤n}\dfrac{H_k}{k} Sn=1≤k≤n∑kHk 的封闭解或值
出处:课本 第六章 课后题 P261 6.26

参考答案:


五、概率生成函数、累积量
考试题目:
(1)求
X
1
+
X
2
+
.
.
.
+
X
n
X_1+X_2+...+X_n
X1+X2+...+Xn 和
n
X
1
nX_1
nX1 的概率生成函数
(2)求
X
1
+
X
2
+
.
.
.
+
X
n
X_1+X_2+...+X_n
X1+X2+...+Xn 和
n
X
1
nX_1
nX1 的第m个累积量
κ
m
κ_m
κm
出处:第八章 课件 8-2 概率生成函数和累积量的定义和性质



4.课程大纲
《具体数学》是高德纳经典著作《计算机程序艺术》的数学预备知识部分的深化和拓展。
第一章:递归
第二章:求和
第三章:整数函数、取整函数,如何处理
第六章:特殊的数
第七章:生成函数 (具体数学 - 组合数学,需要自学)、概率生成函数
第八章:离散的概念、概率

Topics in the Class
- Chap.1 Recurrent Problems
- Chap. 2 Sums
- Chap. 3 Integer Functions
- Chap. 6 Special Numbers
- Chap. 7 Generating Functions
- Chap. 8 Discrete Probabilities
5.教材
Text Book
- Concrete Mathematics—A foundation For Computer Science (第2版)
GRAHAM, KNUTH, PATASHNIK - 中译版(第2版):“具体数学—计算机科学基础”
6.其他课外材料
《计算机编程的艺术》
《算法设计导论》
《组合数学》

7.人物

第一章、递归问题 (Recurrence)
通过3个例子来认识递归问题:
①Hanoi Tower:汉诺塔问题
②Lines in the Plane:n条线可以把区域划分为多少个块
③Josephus Circle:约瑟夫环
这3个例子的3个共同点:
①一直被数学家们反复研究
②已知解法都使用递归,大问题化为小问题
③都可以用计算机程序来求解
具体代码跳转链接:
①https://blog.csdn.net/Edward1027/article/details/136182331
②https://blog.csdn.net/Edward1027/article/details/138280628
1.0 四种方法:求解递归
1.猜
2.变已知问题
3.迭代法
4.成套方法 Set Method
回溯法 Repertoire Method
1.1 汉诺塔问题 Hanoi Tower

补,教材代码
数学归纳:
T0 = 0
T1 = 1。唯一的盘子直接移动到C
T2 = 3。穷举法,第一步必须是小盘子移到B,第二步大盘移到C,第三步小盘移到C。其他所有移法次数都大于3
T3 = 7
…
Tn = Tn-1 +1 + Tn-1 = 2Tn-1 + 1 (把上面n-1个盘当作一个整体先移动到B,最大盘移动到C,n-1个盘作为整体从B移动到C。类似求解T2)
证明: Tn = 2Tn-1 + 1
(1)证明:Tn ≤ 2Tn-1 + 1
由T2,这应该是最小的
(2)证明:Tn ≥ 2Tn-1 + 1
①最大盘移动时,B和C中必然有一根柱子是空的(否则无法移动),所以移动大盘之前至少要Tn-1步,即Tn≥Tn-1
②大盘移动一次,即Tn ≥ Tn-1 + 1。此时状态,大盘在某根柱子上,其他n-1个盘在另一个柱子上
③要达到n个盘子都在同一根柱子上的最终状态,则至少还需要Tn-1步将这n-1个盘子再移动到大盘子上面,即Tn ≥ Tn-1 + 1 + Tn-1 = 2Tn-1 + 1。
即Tn ≥ 2Tn-1 + 1
综上①②所述,Tn = 2Tn-1 + 1
递归方程:
{
T
0
=
0
T
n
=
2
T
n
−
1
+
1
\begin{cases} T_0=0 \\ T_n = 2T_{n-1} +1 \end{cases}
{T0=0Tn=2Tn−1+1
解得:
T
n
=
2
n
−
1
T^n=2^n-1
Tn=2n−1
Hanoi代码:(条件:盘子可以直接从A移动到C)
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
void Hanoi(int n, char start, char middle, char target) {
//1.边界条件
if (n == 1) {
printf("%c -> %c\n", start, target);
return;
}
//2.递归公式
Hanoi(n - 1, start, target, middle); //将上面n-1个盘子从start,经过target,移动到middle上
printf("%c -> %c\n", start, target); //将最大的盘子从start直接移动到target上
Hanoi(n - 1, middle, start, target); //将上面n-1个盘子从middle,经过start,移动到target上
}
int main(void) {
int n;
printf("Please enter the number of plates in Hanoi Tower:");
scanf("%d", &n);
printf("Total steps: %lld\n", (1LL << n) - 1);
Hanoi(n, 'A', 'B', 'C'); //打印移动步骤
return 0;
}
1.2 平面中的直线 Lines in the Plane

当 n=0 时,平面被划分成 1 个区域。
当 n=1 时,平面被划分成 2 个区域。
当 n=2 时,平面被划分成 4 个区域。
当 n=3 时,平面被划分成 7 个区域。
当 n=4 时,平面被划分成 11 个区域。
证明:
Ln ≤ Ln-1+n
Ln ≥ Ln-1+n
得
L
n
=
L
n
−
1
+
n
L_n = L_{n-1}+n
Ln=Ln−1+n
L ( n ) = n ( n + 1 ) 2 + 1 L(n)=\dfrac{n(n+1)}{2}+1 L(n)=2n(n+1)+1
1.3 约瑟夫环问题 Josephus

思考:


人数为偶数,幸存者编号变化:
J
(
2
n
)
=
2
J
(
n
)
−
1
J(2n) = 2J(n)-1
J(2n)=2J(n)−1
人数为奇数,幸存者编号变化:
J
(
2
n
)
=
2
J
(
n
)
+
1
J(2n) = 2J(n)+1
J(2n)=2J(n)+1

2
m
≤
n
<
2
m
+
1
n
=
2
m
+
l
2^m≤n<2^{m+1} \\[5mm] n=2^m+l
2m≤n<2m+1n=2m+l
例如:
7 = 22 + 3
10 = 23 + 2

每隔一人,淘汰一人的约瑟夫环代码:
#include <stdio.h>
int Joseph(int n){
//1.边界条件
if(n == 1 || n == 2){
return 1;
}
//2.递归公式
if(n % 2 == 0){
return 2 * Joseph(n/2) - 1; //偶数
}else{
return 2 * Joseph(n/2) + 1; //奇数
}
}
int main(){
printf("Every other person, one person out. Please enter the initial headcount of players: "); //每隔一个人,淘汰一个人,请输入初始玩家总人数
fflush(stdout); //强制刷新输出缓冲区,使得printf的内容立即输出
int n;
scanf("%d",&n);
printf("The surviving player number is: %d\n",Joseph(n)); //存活的玩家编号
return 0;
}
每隔m人,淘汰一人的约瑟夫环代码:
#include <stdio.h>
int Joseph_2(int n, int m){
//1.边界条件
if(n == 1){
return 0; //从0开始编号
}
//2.递归公式
return (Joseph_2(n-1,m) + m) % n;
}
int main() {
printf("请输入初始玩家人数n: ");
fflush(stdout);
int n;
scanf("%d",&n);
printf("每隔m个人,出局一个人。请输入m的值: ");
fflush(stdout);
int m;
scanf("%d",&m);
printf("存活玩家编号:%d",Joseph_2(n,m) + 1);
return 0;
}
1.4 第一章作业

第二章、求和问题
2.1 表示法
两种∑表示法:
①定界形式: ∑ k = 1 n a k \sum\limits_{k=1}^na_k k=1∑nak
②一般形式: ∑ 1 ≤ k ≤ n a k \sum\limits_{1≤k≤n}a_k 1≤k≤n∑ak


2.2 和与递归
1.和与递归 (Sums and Recurrences)
求和问题转换为递归问题,然后用第一章的4种求解递归问题的方法。
{ S 0 = a + b 0 S n = S n − 1 + a + b n \begin{cases} S_0=a+b_0 \\ S_n=S_{n-1}+a+b_n\\ \end{cases} {S0=a+b0Sn=Sn−1+a+bn
{ R 0 = α R n = R n − 1 + β + γ n \begin{cases} R_0=α \\ R_n=R_{n-1}+β+γ_n\\ \end{cases} {R0=αRn=Rn−1+β+γn
R n = A ( n ) α + B ( n ) β + C ( n ) γ R_n=A(n)α+B(n)β+C(n)γ Rn=A(n)α+B(n)β+C(n)γ
2.成套法

3.快速排序的平均时间复杂度证明

{ C 0 + C n − 1 . . . C n − 1 + C 0 \begin{cases} C_0+C_{n-1} \\ ... \\ C_{n-1}+C_0\\ \end{cases} ⎩ ⎨ ⎧C0+Cn−1...Cn−1+C0
2 n ∑ k = 0 n − 1 C k \dfrac{2}{n}\sum\limits_{k=0}^{n-1}C_k n2k=0∑n−1Ck
2+n-1 = n+1



2.3 和上的运算

1.扰动法


2.Iverson 标记 (Iverson notation)
(1)定义
艾弗森记号 (Iverson bracket,艾弗森括号、艾弗森约定) 是一种将布尔值转换为整数值的表示方法。
它以计算机科学家肯尼斯·艾弗森 (Kenneth E. Iverson) 命名。
目的是将条件表达式转化为一个数值。通过这种方式,复杂的条件判断可以被简洁地表示为数值1(真)或0(假),从而更容易在数学推导和计算中使用。
(2)Iverson标记的基本形式
Iverson约定的基本形式是:
[
P
]
[P]
[P]

其中,P表示一个逻辑条件。
- 如果条件P成立(即条件为真),则表达式P的值为1。
- 如果条件P不成立(即条件为假),则表达式P的值为0。
若 [ P ] [ Q ] = [ P ′ ] [ Q ′ ] [P][Q]=[P'][Q'] [P][Q]=[P′][Q′]
即 P a n d Q ⇔ P ′ a n d Q ′ P\ and\ Q \Leftrightarrow P'\ and\ Q' P and Q⇔P′ and Q′
例如:

两个指标的∑很难做,要转换为一个∑的: ∑ j ⋅ ∑ k = ∑ j , k \sum\limits_j·\sum\limits_k=\sum\limits_{j,k} j∑⋅k∑=j,k∑
(2)Iverson标记的应用
Iverson标记常用于求和式(如Sigma符号)中,特别是在计数、数列和组合问题中,它可以将条件筛选的逻辑简洁地转化为数值。例如,考虑求和式:
∑
n
=
1
1000
[
n
是偶数
]
\sum_{n=1}^{1000}[n是偶数]
n=1∑1000[n是偶数]
这个求和式的含义是:对于从1到1000的每个数字n,判断n是否是偶数。如果是偶数,则该项为1,否则为0。最终的结果是偶数的个数。
2.4 多重和
1.定义
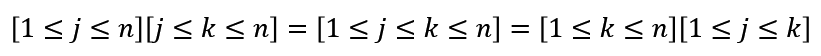

例3:


2.切比雪夫单调不等式

3.多重和中的交换律
(1)调和级数 H(x)
1.调和级数H(x)的定义:
H
(
x
)
=
1
1
+
1
2
+
.
.
.
+
1
x
=
∑
k
=
1
x
1
k
H(x)=\dfrac{1}{1}+\dfrac{1}{2}+...+\dfrac{1}{x}=\sum\limits_{k=1}^x\dfrac{1}{k}
H(x)=11+21+...+x1=k=1∑xk1
2.调和级数H(x)的前向差分:
Δ
H
(
x
)
=
H
(
x
+
1
)
−
H
(
x
)
=
1
x
+
1
ΔH(x)=H(x+1)-H(x)=\dfrac{1}{x+1}
ΔH(x)=H(x+1)−H(x)=x+11
即,每增加一项,调和数增加的量正好为新加入项的倒数
(2)多重和例子

第三种方法,可以求出封闭解

4.封闭解
1.封闭解的定义
封闭解 (Closed-form solution) 指的是可以用有限次运算(包括基本算术运算、指数、对数、三角函数等)直接表示的数学问题的精确解。
也就是说,封闭解不需要通过迭代、逼近或数值方法,而是用已知的函数和有限步骤直接表达出问题的解。
封闭解(Closed-form solution)是指一个数学问题的解可以表示为有限个标准数学运算(如加法、乘法、除法、指数、对数等)的组合,而不需要通过数值计算或迭代过程来求解。封闭解通常表现为一个具体的数学表达式,它给出了解的精确形式,不依赖于近似或数值方法。
2.封闭解的特点:
①精确表示:封闭解是一个明确的、可以直接计算的数学表达式,通常通过标准数学运算表示。
②有限的步骤:它不依赖于无限过程或逐步逼近,因此在计算上是有限的和直接的。
③无需迭代:封闭解不需要使用如牛顿法、梯度下降法等数值迭代方法。

总之,封闭解就是一种能通过明确的数学表达式一次性精确表示出来的解法。
2.5 一般方法总结
1.迭代法
2.扰动法
(1)概念
扰动法(Perturbation Method)是一种用来求解非线性或复杂数学问题的近似解法,尤其适用于那些无法精确求解的微分方程、代数方程或优化问题。其基本思想是将问题的解表示为一个小参数的级数展开,利用已知的简单解来逐步逼近复杂问题的解。
扰动法是一种强有力的工具,特别是在处理一些难以通过直接求解获得精确解的问题时。它通过引入一个小参数,将复杂问题分解为易于处理的近似问题,从而可以得到高效的近似解。
扰动法是一种用来求解复杂问题的近似方法,特别适用于那些直接求解起来很难或无法求解的问题。通俗来说,扰动法就像是在复杂问题的基础上加上一点小的调整(扰动),然后利用这些小的调整来逐步找到一个比较简单的解决方案。
假设你有一个很复杂的数学问题,直接求解非常困难,甚至没有明确的解。这时候,你可以假设问题中有一些“小的偏差”或“小的影响”,这些小的偏差不会大幅改变问题的本质。通过考虑这些小的偏差,你可以把问题简化,从而得到一个相对简单的近似解。
(2)步骤



(3)例子



3.成套法
自己看,上来讲
(1)概念
成套法(Method of Characteristics)是一种常用于求解偏微分方程(PDE)的问题,特别是处理一类特殊的偏微分方程,如一阶偏微分方程。成套法的基本思想是通过将偏微分方程转化为一组常微分方程,从而简化求解过程。
成套法的核心思想是通过沿着某些特殊的曲线(称为特征线)来简化问题。对于给定的偏微分方程,通过在特征线上的积分,可以将偏微分方程转化为常微分方程,从而更容易求解。
成套法通过将偏微分方程转化为常微分方程,并沿着特定的特征线进行求解,从而简化了复杂问题的解决过程。它特别适用于一阶偏微分方程,广泛应用于物理学、工程学等领域的传播和流动问题。
(2)步骤

特征线的直观理解:
特征线可以被看作是某个物理过程中的信息传播路径。在流体力学中,这些特征线代表了粒子的轨迹;在其他领域,这些特征线通常代表了信息的传播或波动的轨迹。成套法利用特征线上的解的传播性质,简化了复杂的偏微分方程。
(3)应用
成套法应用:
成套法主要用于求解类型如下的一阶偏微分方程:
- 输运方程:描述物质、能量、信息等随时间和空间传播的方程。
- 波动方程:描述波的传播,如声波、光波等。
- 流体力学中的方程:例如,描述气体动力学的方程。
(4)例子

4.积分替换
5.展开和收缩
k 2 = ∑ 1 ≤ j ≤ k k k^2=\sum\limits_{1≤j≤k}k k2=1≤j≤k∑k
所以 ∑ 1 ≤ k ≤ n k 2 = ∑ 1 ≤ k ≤ n ∑ 1 ≤ j ≤ k k \sum\limits_{1≤k≤n}k^2=\sum\limits_{1≤k≤n}\sum\limits_{1≤j≤k}k 1≤k≤n∑k2=1≤k≤n∑1≤j≤k∑k
6.有限积分
7.母函数法
留作课外学习,上来讲
2.6 有限与无限微积分
有限与无限微积分 (Finite and Infinite Calculus)
1.差分算子

阶乘幂

2.差和分

3.定和分
(1)定义

(2)性质


(3)公式
∑ a b + 1 g ( x ) δ x = ∑ a b g ( x ) δ x + g ( b ) \sum\limits_a^{b+1}g(x)δx=\sum\limits_a^bg(x)δx+g(b) a∑b+1g(x)δx=a∑bg(x)δx+g(b)
请证明:
∑
a
b
g
(
x
)
δ
x
=
∑
k
=
a
b
−
1
g
(
k
)
=
∑
a
≤
k
<
b
g
(
k
)
\sum\limits_a^bg(x)δx=\sum\limits_{k=a}^{b-1}g(k)=\sum\limits_{a≤k<b}g(k)
a∑bg(x)δx=k=a∑b−1g(k)=a≤k<b∑g(k)
证:
∑
a
b
g
(
x
)
δ
x
=
∑
a
b
−
1
g
(
x
)
δ
x
+
g
(
b
−
1
)
=
∑
a
b
−
2
g
(
x
)
δ
x
+
g
(
b
−
2
)
+
g
(
b
−
1
)
=
.
.
.
=
∑
a
a
g
(
x
)
δ
x
+
g
(
a
)
+
g
(
a
+
1
)
+
.
.
.
+
g
(
b
−
1
)
=
0
+
∑
k
=
a
b
−
1
g
(
k
)
=
∑
a
≤
k
<
b
g
(
k
)
\sum\limits_a^bg(x)δx\\=\sum\limits_a^{b-1}g(x)δx+g(b-1)\\=\sum\limits_a^{b-2}g(x)δx+g(b-2)+g(b-1)\\=...\\=\sum\limits_a^ag(x)δx+g(a)+g(a+1)+...+g(b-1)\\=0+\sum\limits_{k=a}^{b-1}g(k)\\=\sum\limits_{a≤k<b}g(k)
a∑bg(x)δx=a∑b−1g(x)δx+g(b−1)=a∑b−2g(x)δx+g(b−2)+g(b−1)=...=a∑ag(x)δx+g(a)+g(a+1)+...+g(b−1)=0+k=a∑b−1g(k)=a≤k<b∑g(k)
(4)定和分性质的应用
①下降阶乘幂
下降阶乘幂 (Falling Factorial) 在组合数学和离散数学中是一个非常常用的概念,它表示一个从x开始连续递减的乘积。具体定义如下:


下降阶乘在组合计算、级数展开以及多项式插值等问题中都有重要的应用。
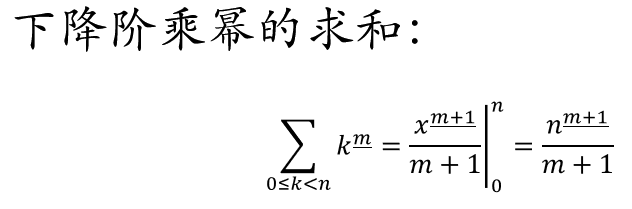

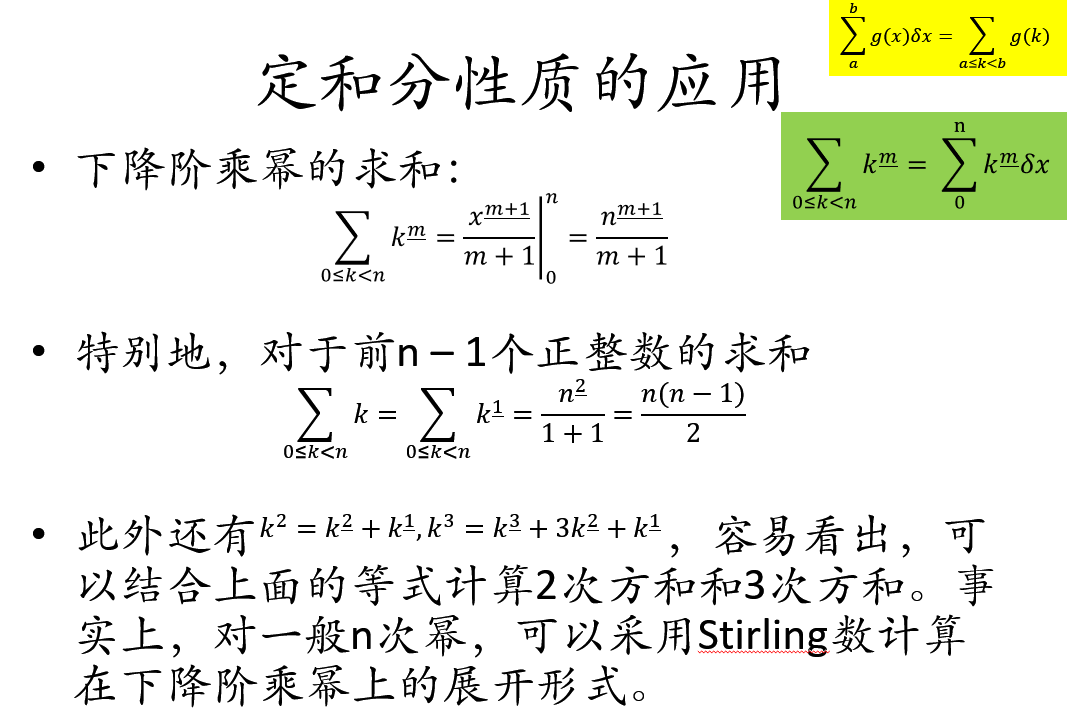
完整描述:

②上升阶乘幂
上升阶乘幂 (Rising Factorial,又称Pochhammer符号),定义为:
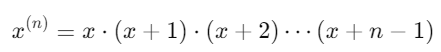
总结:下降阶乘幂提供了一种便捷的方式来表示连续递减的乘积,上升阶乘幂是一种表示连续递增的乘积,在数学的多个领域中起到重要作用。
③基于定和分的几何级数求和

4.差分和逆差分
(1)定义
1.差分
(1)差分用于描述离散数列中相邻元素之间的变化量。对于数列
{
a
n
}
\{a_n\}
{an},其一阶差分定义为:
Δ
a
n
=
a
n
+
1
−
a
n
Δa_n=a_{n+1}-a_n
Δan=an+1−an
(2)高阶差分则是对一阶差分继续求差,例如二阶差分:
Δ
2
a
n
=
Δ
(
Δ
a
n
)
=
Δ
a
n
+
1
−
Δ
a
n
Δ^2a_n=Δ(Δa_n)=Δa_{n+1}-Δa_n
Δ2an=Δ(Δan)=Δan+1−Δan
差分运算在离散数学和数值分析中具有重要意义,其性质与微分运算相似。
2.逆差分
逆差分是差分运算的逆过程,用于从差分序列恢复原始数列。类似于微积分中的不定积分,逆差分通过已知的差分值,逐步推导出原始数列的值。
具体而言,若已知数列 { a n } \{a_n\} {an}的一阶差分 { Δ a n } \{Δa_n\} {Δan},则可以通过以下递推关系恢复原始数列: a n + 1 = a n + Δ a n a_{n+1}=a_n+Δa_n an+1=an+Δan
(2)一些有用的差分和逆差分

第三章、整数函数
整数函数 (Integer Functions)
实数->整数转换:上取整、下取整、模运算
3.1 上取整和下取整
上取整和下取整 (Floors and Ceilings)
1.性质
若f(x)单调连续,则有:
f
(
⌊
x
⌋
)
=
⌊
f
(
x
)
⌋
f(⌊x⌋)=⌊f(x)⌋
f(⌊x⌋)=⌊f(x)⌋

上下取整的基本规则:
这些规则可以用于较为严格地证明关于取整函数的命题:

3.2 底和顶的应用
底和顶的应用 (Floor/Ceiling Applications)

1.期末考试题1:轮盘赌
(1)原题: ⌊ n 3 ⌋ ∣ n ⌊ \sqrt[3]{n}⌋ | n ⌊3n⌋∣n

我手敲的解析答案:






(2)期末变式题: ⌊ n 2 ⌋ ∣ n ⌊ \sqrt[2]{n}⌋ | n ⌊2n⌋∣n

(3)轮盘赌的推广:1000换为N

K ≤ N 3 < K + 1 K≤\sqrt[3]{N}<K+1 K≤3N<K+1
2.实数谱


3.3 下取整/上取整的递归
下取整/上取整的递归 (Floor/Ceiling Recurrences)






3.4 模运算
1.‘MOD’: The Binary Operation ‘MOD’: 二元运算


3.5 底/顶求和 (Floor/Ceiling Sums)
(0)期末考试题2:根号求和,改为立方根求和

(1)原题:平方根向下取整求和


(2)考试变式题:立方根向下取整求和

第六章、特殊的数
第六章自学,“考试一定会考到” 考试内容限于PPT内容
第七章、生成函数
1.概率生成函数
第八章、离散概率 Discrete Probability
- 概率和统计的观点,或者说随机的观点,是革命性的科学方法,在物理、天文、化学、生物和金融等领域取得了广泛的应用,带来了巨大的冲击。
- 从个人科学素养来说,随机方法及其观点可以带来显著的境界提升。另一方面,随机数学的合理性却是一个哲学问题……
- 本章讨论离散空间下的概率问题,基本上仅涉及离散求和,而非积分计算。将会较多地运用前面所学的求和等方法。
1.概念与定义

.概率空间

2.概率事件

3.随机变量

4.联合分布

5.均值(数学期望)、中位数、众数

期末考试题3:证明最后一行

2.均值与方差
方差variance定义为
𝑉
𝑋
=
𝐸
(
(
𝑋
−
𝐸
𝑋
)
2
)
𝑉𝑋=𝐸((𝑋−𝐸𝑋)^2 )
VX=E((X−EX)2)
方差又称离差,即随机变量远离均值的差。直观上看,方差描述了随机变量分布的“展开程度”。

期末考试题3:证明红框部分

切比雪夫不等式


3.概率生成函数


期末考试题目5:概率生成函数
证明上图: G X ( Z ) = E ( Z X ) G_X(Z)=E(Z^X) GX(Z)=E(ZX)

一般累积量






























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










