归并排序（代码+详解）

Enthusiastic_boy

已于 2022-03-06 20:06:58 修改

阅读量1w

点赞数 6

文章标签：排序算法算法数据结构 c++ c语言

于 2022-01-27 15:58:22 首次发布

本文链接：https://blog.csdn.net/Enthusiastic_boy/article/details/122714772

版权

基本思想

归并排序（MERGE-SORT）是建立在归并操作上的一种有效的排序算法,该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。

代码

合并两组有序序列

从以上图中可以看出，归并排序就是不断的将两组有序的序列进行合并（第一次将单独的一个元素当作一组有序序列），从而得到最终的排序结果。所以首先给出如下一段代码，用来合并两组有序的序列（排升序）：

void MergeData(int* arr,int left,int mid,int right,int* s){//对两组有序序列进行归并
    int begin1=left;//第一组序列的首元素下标
    int end1=mid-1;//第一组序列最后元素下标
    int begin2=mid;//第二组序列首元素下标
    int end2=right-1;//第二组序列最后元素下标
    int count=left;//进行归并时第一个元素应放在对应的位置
    while(begin1<=end1&&begin2<=end2){//归并两组序列
        if(arr[begin1]<=arr[begin2]){
            s[count]=arr[begin1];
            begin1++;
        }else{
            s[count]=arr[begin2];
            begin2++;
        }
        count++;
    }
    while(begin1<=end1){//如果第一组序列有剩余，继续归并
        s[count]=arr[begin1];
        count++;
        begin1++;
    }
    while(begin2<=end2){//如果di二组序列有剩余，继续归并
        s[count]=arr[begin2];
        count++;
        begin2++;
    }
}

以上代码中，因为合并时数字都在同一数组当中，所以它们的下标是连续的，在合并时需要使用新的空间来放合并后的结果，注意：合并后的结果应该放在新申请出的空间的对应位置，即count必须从left开始，因为在以下代码中需要拷贝。

归并排序

1.递归

有了上述合并两组有序序列的代码，那么很容易就会想到使用递归来对一组序列进行归并，直接看代码：

void MergeSort(int* arr,int left,int right,int* s){//归并排序递归
    if(right-left<=1){//元素个数小于1，直接返回
        return;
    }
    int mid=left+(right-left)/2;
    MergeSort(arr,left,mid,s);//归并左半部分
    MergeSort(arr,mid,right,s);//归并右半部分
    MergeData(arr,left,mid,right,s);//将当前有序的序列进行归并
    memcpy(arr+left,s+left,sizeof(arr[0])*(right-left));//将归并后的将结果拷贝回原来的数组，为下次归并做准备

}

上述递归过程中不断将问题的规模缩小，直到对两个元素进行排序，而后在层层处理其余部分。归并排序的递归格式有点像二叉树的后序遍历，很方便记忆。注意：每次归并完一组数据，都要把归并好的结果拷贝回原来的空间,还要注意当前拷贝的位置与拷贝的元素个数。

2.循环

递归可能不是很好理解，但是循环就比较简单了。可以先两个一组进行归并，全部归并完成后，在四个四个一组进行归并..........代码如下：

void MergeSortNonR(int* arr,int size){
    int* s=(int*)malloc(sizeof(arr[0])*size);
    int gap=1;//相当于第一次每一个为一组
    while(gap<size){
        int i=0;
        for(;i<size;i+=2*gap){
            int left=i;
            int mid=left+gap;
            if(mid>size){//越界，进行复位
                mid=size;
            }
            int right=mid+gap;
            if(right>size){
                right=size;
            }
            MergeData(arr,left,mid,right,s);
        }
        gap*=2;
        memcpy(arr,s,sizeof(arr[0])*size);//拷贝
    }
}

当gap=1时，此时每两个元素一组，把这两个元素进行了排序，然后不断将数组元素划分为两个一组，全部排序。到下一次gap就会增长2倍，此时四个元素一组，重复上述过程。直到gap>size，说明整个归并排序结束。注意：此时的拷贝只需要在gap变化之后进行整体拷贝。

复杂度与稳定性

时间复杂度

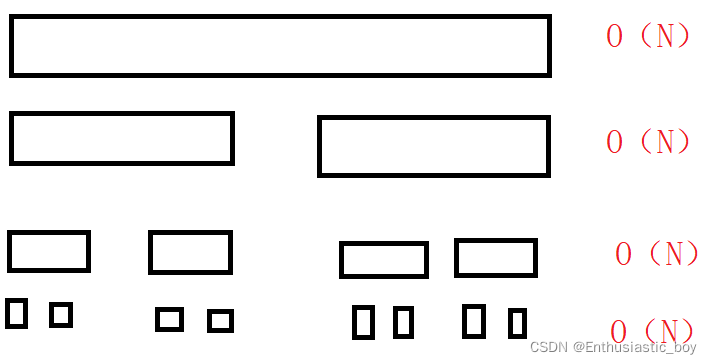
排序的过程像是一颗二叉树，每一层表示归并这层元素，复杂度为O（N），深度为logN,所以整体的时间复杂度为：O（NlogN）

空间复杂度

每次在堆上申请的空间大小与原数组相同，所以空间复杂度为：O（N）

完整代码

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
void MergeData(int* arr,int left,int mid,int right,int* s){//对两组有序序列进行归并
    int begin1=left;//第一组序列的首元素下标
    int end1=mid-1;//第一组序列最后元素下标
    int begin2=mid;//第二组序列首元素下标
    int end2=right-1;//第二组序列最后元素下标
    int count=left;//进行归并时第一个元素应放在对应的位置
    while(begin1<=end1&&begin2<=end2){//归并两组序列
        if(arr[begin1]<=arr[begin2]){
            s[count]=arr[begin1];
            begin1++;
        }else{
            s[count]=arr[begin2];
            begin2++;
        }
        count++;
    }
    while(begin1<=end1){//如果第一组序列有剩余，继续归并
        s[count]=arr[begin1];
        count++;
        begin1++;
    }
    while(begin2<=end2){//如果di二组序列有剩余，继续归并
        s[count]=arr[begin2];
        count++;
        begin2++;
    }
}
void MergeSort(int* arr,int left,int right,int* s){//归并排序递归
    if(right-left<=1){//元素个数小于1，直接返回
        return;
    }
    int mid=left+(right-left)/2;
    MergeSort(arr,left,mid,s);//归并左半部分
    MergeSort(arr,mid,right,s);//归并右半部分
    MergeData(arr,left,mid,right,s);//将当前有序的序列进行归并
    memcpy(arr+left,s+left,sizeof(arr[0])*(right-left));//将归并后的将结果拷贝回原来的数组，为下次归并做准备

}
void MergeSortNonR(int* arr,int size){
    int* s=(int*)malloc(sizeof(arr[0])*size);
    int gap=1;//相当于第一次每一个为一组
    while(gap<size){
        int i=0;
        for(;i<size;i+=2*gap){
            int left=i;
            int mid=left+gap;
            if(mid>size){//越界，进行复位
                mid=size;
            }
            int right=mid+gap;
            if(right>size){
                right=size;
            }
            MergeData(arr,left,mid,right,s);
        }
        gap*=2;
        memcpy(arr,s,sizeof(arr[0])*size);//拷贝
    }
}
void Print(int* arr,int size){
    int i=0;
    for(;i<size;i++){
        printf("%d ",arr[i]);
    }
    printf("\n");
}
int main(){
    int arr[]={5,7,1,3,9,8,0,2,4,6};
    //int* s=(int*)malloc(sizeof(arr));
    //MergeSort(arr,0,sizeof(arr)/sizeof(arr[0]),s);
    MergeSortNonR(arr,sizeof(arr)/sizeof(arr[0])); 
    Print(arr,sizeof(arr)/sizeof(arr[0]));
    return 0;
}